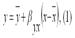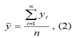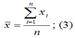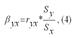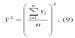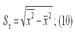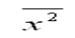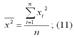Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β0 и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) ỹ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

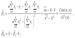
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:

где

– среднее значение зависимой переменной;

– среднее значение независимой переменной;

– среднее арифметическое значение произведения зависимой и независимой переменных;

– дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии осуществим иной подход к решению данной проблемы.

Линейная модель парной регрессии может быть записана в виде:

где у – значения зависимой переменной;

х – значения независимой переменной;

– среднее значение зависимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:

уi – значения зависимой переменной,

n – объём выборки;

– среднее значение независимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:

Параметр βyx называется выборочным коэффициентом регрессии переменной у по переменной х. Данный параметр показывает, на сколько в среднем изменится зависимая переменная у при изменении независимой переменной х на единицу своего измерения.

Выборочный коэффициент регрессии переменной у по переменной х рассчитывается по формуле:

где ryx – это выборочный парный коэффициент корреляции между переменными у и х, который рассчитывается по формуле:

– среднее арифметическое значение произведения зависимой и независимой переменных:

Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:

– среднее значение из квадратов значений зависимой переменной у:

– квадрат средних значений зависимой переменной у:

Sx – показатель выборочного среднеквадратического отклонения независимой переменной х. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения независимой переменной х от её среднего значения. Они рассчитывается по формуле:

– среднее значение из квадратов значений независимой переменной х:

– квадрат средних значений независимой переменной х:

При использовании рассмотренного подхода оценивания неизвестных параметров линейной модели парной регрессии, следует учитывать что ryx=rxy, однако βyx≠βxy.