Адекватность трендовой модели

Трендовая модель считается адекватной описываемому процессу, если значения случайной остаточной компоненты εt являются случайными центрированными некоррелированными нормально распределёнными величинами. Проверка адекватности модели состоит в проверке указанных свойств ряда остатков модели.

Проверка случайности остатков модели осуществляется с помощью критериев исследования временного ряда на предмет наличия в нём трендовой компоненты:

1) критерий, основанный на сравнении средних уровней временного ряда;

2) критерий «восходящих и нисходящих» серий;

3) критерий серий, основанный на медиане выборочной совокупности.

В этом случае вместо исходных уровней временного ряда y1,y2,…,yt используются элементы остаточного ряда e1,e2,…,et.

Также проверка случайности остатков модели может осуществляться с помощью критерия поворотных точек.

При использовании критерия поворотных точек остаток модели et сравнивается с двумя соседними элементами ряда. Если он окажется меньше или больше их, то данная точка является поворотной. В конце сравнений подсчитывается количество m всех поворотных точек. Ряд остатков модели считается случайным, если выполняется условие:

где N – объём выборочной совокупности.

Проверка центрированности остатков временного ряда осуществляется с помощью t-критерия Стьюдента.

Основная гипотеза формулируется как утверждение о центрированности ряда остатков.

Критическое значение t-критерия tкрит(α/2, N-1) определяется для уровня значимости α/2 и числа степеней свободы (N-1) по таблице распределения Стьюдента.

Наблюдаемое значение t-критерия рассчитывается по формуле:

где

– среднее арифметическое значение ряда остатков:

G(e) – среднеквадратическое отклонение ряда остатков:

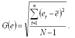
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. t набл ›t крит, то основная гипотеза отвергается. Следовательно, ряд остатков является не центрированным.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл≤tкрит, то основная гипотеза принимается. Следовательно, ряд остатков является центрированным.

Проверка независимости ряда остатков модели осуществляется с целью определения возможной систематической составляющей в составе ряда остатков. Если модель подобрана неудачно, то остатки будут подвержены автокорреляционной зависимости.

Независимость остатков проверяется с помощью критерия Дарбина-Уотсона, связанного с гипотезой о наличии в ряде остатков автокорреляции первого порядка, т. е. о корреляционной зависимости соседних остатков.

Нормальность ряда остатков проверяется с помощью показателей асимметрии и эксцесса (если объём выборочной совокупности не превышает 50 значений). При нормальном распределении показатели асимметрии и эксцесса равны нулю.

На основании выборочных данных вычисляются эмпирические коэффициенты асимметрии и эксцесса по формулам:

Если вычисленные коэффициенты близки к нулю, то можно сделать вывод, что ряд остатков подчиняется нормальному закону распределения.

В дополнение к выборочным коэффициентам асимметрии и эксцесса рассчитывают показатели среднеквадратических отклонений данных коэффициентов по формулам:

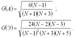
Если одновременно выполняются следующие неравенства:

1) |КА|≤1,5G(A);

2) |КЭ|≤1,5G(Э),

то гипотеза о нормальном характере распределения случайной компоненты принимается. Если хотя бы одно из указанных неравенств нарушается, то гипотеза о нормальном распределении остатков отвергается.

Помимо адекватности выбранной модели, необходимо охарактеризовать её точность. Наиболее простым критерием точности модели является относительная ошибка, рассчитываемая по формуле:

Если относительная ошибка равна менее, чем 13 %, то точность подобранной модели признаётся удовлетворительной.