В чем роль теоретической (гипотетической) регрессии в прикладном эконометрическом анализе?

Теоретическая (гипотетическая) регрессия позволяет производить теоретические расчеты (имеется в виду оценка последствий изменений значения какой-то объясняющей переменной), а также она используется для прогнозирования значений зависимой переменной.

Теоретическая регрессия:

Y=a+b*x+u, где u – случайный член

В регрессионном анализе изучается связь и определяется количественная зависимость между зависимой переменной и одной или несколькими независимыми переменными. Пусть переменная Y зависит от одной переменной . При этом предполагается, что переменная принимает заданные фиксированные значения, а зависимая переменна Y имеет случайный разброс из-за ошибок измерения, влияния неучтенных факторов и т.д. Предположим, что Y в "среднем" линейно зависит от значений переменной .

Таким образом, существуют наблюдаемые значения х и у, между ними предполагается линейная связь. Если бы соотношение между х и у было точно, то все наблюдаемые точки лежали на одной прямой Y=a+b*x. Однако истинные значения у отклоняются от этой прямой на величину случайного члена.

Таким образом, теоретическая регрессия необходима для оценки взаимосвязи между переменными. На основе n наблюдений строится расчетная регрессия, оцениваются коэффициенты а и b.

Почему расчетная регрессия не совпадает с теоретической?

Из-за наличия случайного члена невозможно рассчитать истинные значения b,α при попытке построить прямую и определить положение линии регрессии. т.к. остатки не совпадают со значениями случайного члена

6. В чем состоит разница между случайном членом регрессии и остатками в регрессионном анализе?

Случайный член указывает на то, что существует случайная составляющая, которая влияет на зависимую переменную; остаток- измеренная величина отклонения между фактическим и расчетным значением переменной.

Случайный член (u_i) включается в регрессию для подтверждения существования случайного фактора, оказывающего влияние на зависимую переменную. Y_i=β₁+β₂X_i+u_i

Остаток (e_i) – измеримая разность между действительной величиной Y в соответствующем наблюдении и расчетным значением по регрессии. e_i=Y_i-

В чем состоит идея метода наименьших квадратов?

Идея МНК основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т.е. нужно оценить параметры о функции f(a,x) таким образом, чтобы ошибки еi= уi-f(а,х), точнее - их квадраты, по совокупности были минимальными. Для этого нужно решить задачу минимизации суммы квадратов остатков S=e12+..+en2

В чем состоят основные достоинства и недостатки метода наименьших квадратов с точки зрения прикладной эконометрики?

Достоинства:

1. Наиболее простой метод выбора значений b₁ и b₂, чтобы остатки были минимальными;

2. При выполнении условий Гаусса-Маркова МНК-оценки будут наилучшими (наиболее эффективными) линейными (комбинации Y_i) несмещёнными оценками параметров регрессии (b₁ и b₂₎.

Условия Гаусса-Маркова:

- модель линейна по параметрам и правильно специфицирована;

- объясняющая переменная в выборке имеет некоторую вариацию;

- математическое ожидание случайного члена равно нулю;

- случайный член гомоскедастичен;

- значения случайного члена имеют взаимно независимые распределения;

- случайный член имеет нормальное распределение

Недостатки: МНК-оценки являются эффективными линейными несмещёнными ТОЛЬКО при выполнении ВСЕХ условий Гаусса-Маркова, что на практике встречается редко.

Как получить уравнения метода наименьших квадратов, используя производные?

y=a+bx; S²=∑(y_i-a-bx_i)²=> (S²)_a^’=0 и (S²)_b^’=0

Как выписать уравнения метода наименьших квадратов, не используя производные?

11. Пусть выборка состоит из трех точек (x 1, y 1), (x 2, y 2), (x 3, y 3). Как вывести уравнения метода наименьших квадратов, используя условия первого порядка для производных.

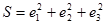
Как коэффициенты регрессии выражаются через основные статистические характеристики выборки (среднее, дисперсия, ковариацию и др.).

Вывод формул для оценки коэффициентов (для парной регрессии) в лекции 3.