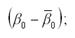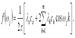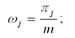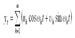Сезонные фиктивные переменные

Метод сезонных фиктивных переменных относится к методам моделирования сезонных компонент временного ряда. Суть данного метода заключается в построении модели регрессии, которая наряду с фактором времени включает сезонные фиктивные переменные.

Фиктивной переменной (dummy variable) называется атрибутивный или качественный фактор, представленный с помощью определённого цифрового кода.

Моделью регрессии с переменной структурой называется модель регрессии, включающая в качестве факторной (факторных) переменных фиктивную переменную.

Предположим, что задача состоит в исследовании временного ряда Xij, где i – это номер сезона (периода времени внутри года, например, месяца или квартала),

L – число сезонов в году, j – номер года,

m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m.

При построении модели регрессии с переменной структурой необходимо учитывать, что число сезонных фиктивных переменных всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L-1. Например, при моделировании годовых данных модель регрессии помимо фактора времени должна содержать одиннадцать фиктивных компонент (12-1). При моделировании поквартальных данных модель регрессии должна содержать три фиктивные компоненты (4-1) и т. д.

Каждому из сезонов соответствует определённое сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, является базой сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Например, если имеются поквартальные данные, то значения фиктивных переменных D2,D3,D4 будут принимать следующие значения для каждого из кварталов:

Тогда общий вид модели регрессии с переменной структурой будет иметь вид:

yt=β0+ β1*t+δ2*D2+δ3*D3+δ4*D4+εt.

Данная модель регрессии представляет собой одну из разновидностей аддитивной модели временного ряда.

На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала:

yt=β0+ β1*t+εt.

Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии:

1) частная модель регрессии для второго квартала:

yt=β0+ β1*t+δ2+εt;

2) частная модель регрессии для третьего квартала:

yt=β0+ β1*t+δ3+εt;

3) частная модель регрессии для четвёртого квартала:

yt=β0+ β1*t+δ4+εt.

Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi.

Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции.

Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей.

Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле:

Для поквартальных данных оценка сезонных отклонений осуществляется по формулам:

1) оценка сезонного отклонения для первого квартала:

2) оценка сезонного отклонения для второго квартала:

3) оценка сезонного отклонения для третьего квартала:

4) оценка сезонного отклонения для четвёртого квартала:

Сумма сезонных отклонений должна равняться нулю.

Одномерный анализ Фурье

Одним из основных методов моделирования сезонных и циклических колебаний является метод, основанный на применении одномерных рядов Фурье. В свою очередь, ряды Фурье являются одной из разновидностей спектрального анализа.

С помощью спектрального анализа в структуре временного ряда определяется пик отклонений от тренда, что позволяет рассчитать длительность периодической компоненты ряда.

Для того, чтобы к временному ряду можно было применять методы спектрального анализа, его необходимо привести к стационарному виду.

Суть спектрального анализа заключается в том, что случайный стационарный процесс представляется как сумма гармонических колебаний различных частот, называемых гармониками.

Спектром называется функция, которая описывает распределение амплитуд случайного стационарного процесса по различным частотам.

Сезонная компонента временного ряда может быть разложена в ряд Фурье.

Сезонные колебания, разложенные рядом Фурье, представляют собой сумму нескольких синусоидальных и косинусоидальных гармоник с различными периодами:

где uk, υk – некоррелированные случайные величины с нулевым математическим ожиданием и одинаковыми дисперсиями:

D(uk)=D(υk)=Dk;

ωk – длина волны функции синуса или косинуса, называемая частотой.

Частота выражается числом циклов (периодов) в единицу времени.

Цель спектрального анализа временных рядов заключается в оценивании спектра ряда. Спектр временного ряда можно определить как разложение дисперсии ряда по частотам для определения значимых гармоник.

Значение спектра временного ряда рассчитывается по формуле:

где ωj – частоты, для которых оцениваются спектры:

ck – автокорреляционная функция, значения которой рассчитываются по формуле:

λk – специально подобранные веса значений ковариационной функции, зависящие от частоты m, которые называются корреляционным окном.

Корреляционным окном называется преобразованная форма взвешенного скользящего среднего шириной m.

Дисперсия ряда Фурье рассчитывается по формуле:

Дисперсия ряда Фурье равна сумме всех гармоник её спектрального разложения.

Следовательно, дисперсия D(yt) распределена по различным частотам. Графически распределение дисперсии ряда Фурье изображается с помощью периодограммы. Суть анализа периодограммы заключается в определении частоты или периода с наибольшими спектральными плотностями, которые вносят наибольший вклад в периодические колебания временного ряда, что позволит определить его основной период колебания.

Ряд Фурье вида

можно рассматривать как линейную модель множественной регрессии.

Результативной переменной в данной модели будут являться значения временного ряда, а независимыми переменными – функции синусов всех возможных частот. Коэффициенты uk при косинусах и υk при синусах будут представлять собой коэффициенты модели регрессии, которые показывают степень, с которой коррелированности соответствующих функций с исходными данными. Если рассчитанное значение коэффициента при определённом синусе или косинусе достаточно велико, то на соответствующей частоте в исходных данных существует строгая периодичность.