
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Мультиколлинеарность. Фиктивные переменные.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание занятия. 1. Введение фиктивных переменных в уравнение множественной регрессии. 2. Частная корреляция модели множественной регрессии. Литература: [1] стр155-169, [3] стр200-216, стр262-282
Задание 1 Пусть по данным о 20 рабочих цеха оценивается регрессия заработной платы рабочего за месяц от количественного фактора – возраст рабочего (лет) и качественного фактора – пол.
Построить модель множественной регрессии.
Методические указания по выполнению задания: Введем в модель фиктивную переменную z, которая принимает два значения: 1 – если пол рабочего мужской; 0 – если пол женский. Построим модель вида: Для оценки параметров модели используем метод наименьших квадратов. Построим систему нормальных уравнений: В результате решения системы получим оценки: Уравнение регрессии: Интерпретация параметра с=10,32 при фиктивной переменной: у мужчин зарплата в среднем выше, чем у женщин при одном и том же возрасте мужчины и женщины на 10,32$.
Задание №2 Изучается зависимость выработки продукции на одного работника у (тыс. д.ед.) от ввода в действие новых основных фондов х1 (% стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
Определить средние коэффициенты эластичности, частные коэффициентов корреляции.
Методические указания по выполнению задания: Средние коэффициенты эластичности определяются по формуле: Для данного уравнения множественной регрессии (построенном на предыдущем занятии) получим:
С увеличением основных фондов на 1% выработка продукции на одного работника увеличивается на 0,609% при устранении влияния действия удельного веса рабочих высокой квалификации в общей численности рабочих. С увеличением удельного веса рабочих высокой квалификации в общей численности рабочих на 1% выработка продукции на одного работника увеличивается на 0,199% при устранении влияния основных фондов. Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
Сравнивая полученные результаты, видно, что более сильное воздействие на выработку продукции оказывает действие новых основных фондов. Лабораторная работа №8 Тема: Статистическая значимость коэффициентов линейной регрессии. Содержание занятия: 1. Оценить практическую значимость уравнения множественной регрессии через индекс множественной корреляции 2. Оценка значимости уравнения множественной регрессии по F-критерию Фишера. Литература: [1] стр129-141, [3] стр159-163, [4]стр85-86 Задание Изучается зависимость выработки продукции на одного работника у (тыс. д.ед.) от ввода в действие новых основных фондов х1 (% стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
1. Определить линейный коэффициент множественной корреляции. Сделайте вывод. 2. Провести оценку значимости уравнения множественной регрессии по F-критерию Фишера. 1. Линейный коэффициент множественной корреляции определяется следующим образом: Зависимость y от х1 и х2 характеризуется как тесная.
2. Общий F-критерий проверяет гипотезу о статистической значимости уравнения регрессии и показателя тесноты связи:
Табличное значение F-критерия составляет 3,59 (приложение 2). Так как фактическое значение F-критерия Фишера превышает табличное значение, то можно сделать вывод о статистической значимости и надежности построенного уравнения множественной регрессии. Лабораторная работа №9 Тема: Нелинейные эконометрические модели. Содержание занятия: 1. Определение параметров нелинейной регрессии. 2. Оценка качества построенной модели нелинейной регрессии. Литература: [1] стр62-87, [3] стр115-129, [4] стр77-81
Задание Имеются следующие исходные данные:
1. Для характеристики зависимости у от х рассчитать параметры равносторонней гиперболы. 2. Оценить построенную модель через среднюю ошибку аппроксимации
Методические указания по выполнению задания: Уравнение равносторонней гиперболы
Параметры уравнения равносторонней гиперболы определяются следующим образом:
Уравнение равносторонней гиперболы имеет следующий вид: Индекс корреляции: Средняя ошибка аппроксимации составила 30,61; поэтому качество построенной модели оценивается как плохое. Лабораторная работа №10 Тема: Гетероскедастичность Содержание занятия. Применение тестов для оценки гетероскедастичности. Литература: [1] стр155-169, [3] стр200-216, стр262-282
Задание Оценить регрессионную зависимость выпуска продукции обрабатывающей промышленности на душу населения у от валового внутреннего продукта на душу населения х для 17 стран. Исходные данные (усл.ед):
На основе данных с помощью обычного МНК оценить регрессии для шести стран с наименьшими значениями показателя х и для шести стран с наибольшими значениями этого показателя.
Методические указания по выполнению задания: Для установления явления гетероскедастичности существуют ряд тестов: 1) тест Голдфелда-Кванта; 2) тест ранговой корреляции Спирмена; 3) тест Уайта; 4) тест Глезера; 5) тест Парка. Наиболее популярным является тест Голдфелда-Кванта. Данный тест используется для проверки следующего типа гетероскедастичности: когда среднее квадратическое отклонение случайной составляющей Тест Голдфелда-Кванта состоит в следующем: 1) упорядочение п наблюдений по мере возрастания переменной х; 2) исключение из рассмотрения С центральных наблюдений; при этом (п-С):2>р, где р – число оцениваемых параметров; 3) разделение совокупности из (п-С) наблюдений на две группы соответственно с малыми и большими значениями фактора х и определение по каждой из групп уравнений регрессий; 4) определение остаточной суммы квадратов для первой и для второй S2 групп и нахождения их отношения R=S1:S2 (или R=S2:S1, в числителе должна быть наибольшая из сумм квадратов отклонений). При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F -критерию со степенями свободы ((п-С-2р):2) для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F -критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин (если Fтабл > Fкр, то гетероскедастичность имеет место). Применим тест Голдфелда-Кванта. Суммы квадратов отклонений составляют S1=229, S2=9804. При этом S2:S1=9804:229=42,8. Критическое значение Fкр =6,39, при 5-% уровне значимости. Поскольку F= 42,8 > Fкр =6,39, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
Лабораторная работа № 11 Тема: Динамический ряд. Содержание занятия. 1. Расчет автокорреляции уровней временного ряда. 2. Расчет параметров трендов. Литература: [1] стр234-239,[2] стр138-139
Задание №1 Имеются условные данные о средних расходах на конечное потребление (усл. д.ед.) за 8 лет:
Рассчитать коэффициент автокорреляции первого порядка.
Методические указания по выполнению задания: Расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет, поэтому определим коэффициент корреляции между рядами yt и yt-1 и измерим тесноту связи между расходами на конечное потребление текущего и предыдущего годов. Формула для расчета коэффициента корреляции имеет вид: В качестве переменной х рассмотрим ряд y2, y3,…, y8; в качестве переменной y - ряд y1, y2,… y7. Тогда приведенная формула примет вид:
Заполним таблицу:
где Используя формулу, получаем коэффициент автокорреляции первого порядка: Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующих годов и, следовательно, о наличии во временном ряде сильной линейной тенденции. Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Задание №2. Имеются данные об урожайности овощей в хозяйствах области:
1. Построить графики ряда динамики и трендов. 2. Рассчитать параметры уравнений трендов. 3. Выбрать наилучший вид тренда на основании графического изображения и значения коэффициента детерминации. Методические указания по выполнению задания: Построение графиков осуществляется с помощью Мастера диаграмм: 1) введите исходные данные; 2) активизируйте Мастер диаграмм: в главном меню выберите Вставка/Диаграмма 3) в окне Тип выберите График. Щелкните по кнопке Далее. 4) Заполните диапазон данных. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее. 5) Заполните параметры диаграммы на разных закладках: названия диаграммы и осей; подписи данных и др. Укажите место размещения диаграммы на отдельном или на имеющемся листе. Щелкните по кнопке Готово. Линия тренда может быть добавлена в построенный график. Для этого: 1) выделите область построения диаграммы; в главном меню выберите Диаграмма/Добавить линию тренда; 2) в появившемся диалоговом окне выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома. В качестве дополнительной информации на диаграмме следует отобразить уравнение регрессии и значение коэффициента детерминации, установив соответствующие флажки на закладке Параметры. Щелкните по кнопке ОК. Для вышеприведенных исходных данных получены следующие уравнения трендов и значения коэффициента детерминации
Исходные данные лучше всего описывает полином второй степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.
Лабораторная работа №12 Тема: Динамический ряд. Содержание занятия. 1.Построение аддитивной и мультипликативной моделей временного ряда. 2.Прогнозирование по аддитивной и мультипликативной моделям. Литература: [1] стр239-255,[2] стр137 Задание Пусть имеются поквартальные данные о прибыли компании за 3 года.
Построить мультипликативную модель временного ряда и сделать прогноз на последующие два квартала. Методические указания по выполнению задания: Для построения мультипликативной модели временного ряда необходимо: 1) Провести выравнивание временного ряда методом скользящей средней. 2) Найти оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (графа 5). Расчет оценок сезонной компоненты в мультипликативной модели
Найденные оценки используются для расчета сезонной компоненты S. Для этого находятся средние за каждый квартал оценки сезонной компоненты Si. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле (в примере равно 4). Расчет сезонной компоненты
Имеем: 0,9025+1,216+1,0945+0,8055=4,0185. Определим корректирующий коэффициент: k= 4:4,0185=0,9954. Определим скорректированные значения сезонной компоненты, умножив её средние оценки на корректирующий коэффициент 3) Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Получим величины T*E=Yt/Si, которые содержат только тенденцию и случайную компоненту. Расчет выравненных значений Т и ошибок в мультипликативной модели
4) Определить компоненту Т. Для этого рассчитываются параметры линейного тренда, используя уровни (Т*Е). Уравнение тренда имеет следующий вид: Т=87,022-2,076t. Подставляя в это уравнение значения t=1,2,…12 найти уровни Т для каждого момента времени. 5) Найти уровни временного ряда, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов. 6) Расчет ошибки в мультипликативной модели производится по формуле E=Yt-(T*S) (графа 7). Пусть необходимо дать прогноз прибыли в течение первого полугодия следующего года. Прогнозное значение Ft уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компоненты. Для определения трендовой компоненты следует воспользоваться уравнением тренда Т=87,022-2,076t. Т13=87,022-2,076*13=60,034. Т14=87,022-2,076*14=57,958. Значения сезонной компоненты S1=0,8983; S2=1,2104. F13= Т13* S1=60,034*0,8983=53,928 F14= Т14* S2=57,958*1,2104=70,152 Прогноз ожидаемой прибыли компании на первое полугодие составит: 53,928+70,152=124,080 тыс. у.ед. Лабораторная работа № 13 Тема: Динамический ряд. Содержание занятия. 1. Применение методов исключения тенденции. 2. Автокорреляция в остатках. Расчет критерия Дарбина-Уотсона. Литература: [1] стр263-278, [2] стр139-140
Задание. По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия у (млн. тенге) от цен на сырьё х1 (тыс. тенге за 1т) и производительности труда х2 (ед. продукции на 1 работника):
Требуется: 1) по трем позициям рассчитать 2) рассчитать критерий Дарбина-Уотсона. 3) оценить полученный результат при 5-% уровне значимости. Методические указания по выполнению задания: 1)
Остатки Следовательно, Результаты вычислений оформим в таблицу:
2) Критерий Дарбина-Уотсона рассчитывается по формуле: 3) Фактическое значение d сравниваем с табличными значениями при 5-% уровне значимости. При п=18 месяцев и т=2 (число факторов) нижнее значение 4 - d=4-3,81=0,19, что значительно меньше, чем
Лабораторная работа №14
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.81.47 (0.008 с.) |

 .
.

 .
.







 линеаризуется при замене
линеаризуется при замене  . Тогда уравнение примет вид
. Тогда уравнение примет вид  . Для определения параметров уравнения необходимо провести следующие расчеты:
. Для определения параметров уравнения необходимо провести следующие расчеты:


 - связь между рассматриваемыми признаками очень тесная.
- связь между рассматриваемыми признаками очень тесная.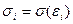 пропорционально значению признака-фактора хi в том наблюдении, т.е.
пропорционально значению признака-фактора хi в том наблюдении, т.е.  .
.
 где
где 




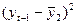

 .
.
 .
.


 или
или



 . При анализе остаточных величин были использованы значения, приведенные в следующей таблице:
. При анализе остаточных величин были использованы значения, приведенные в следующей таблице: .
. .
. определяется путем подстановки фактических значений х1 и х2 в уравнение регрессии:
определяется путем подстановки фактических значений х1 и х2 в уравнение регрессии: ;
;  ;
; 
 рассчитываются по формуле:
рассчитываются по формуле:  .
. ;
;  .
.





 равно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, то можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:
равно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, то можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:


