
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос № 24.4. Оригинальный порядковый номер: 16Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Двухшаговый метод наименьших квадратов определения оценок структурных параметров используется в случае... Варианты ответов. Кол-во правильных ответов - 1 1. неидентифицируемости хотя бы одного уравнения в системе 2. использования в системе фиктивных переменных 3. точной идентифицируемости системы одновременных уравнений или сверхидентифицируемости этой системы 4. отсутствия в системе тождеств Вопрос № 24.5. Оригинальный порядковый номер: 24 Двухшаговый метод наименьших квадратов является частным случаем... Варианты ответов. Кол-во правильных ответов - 1 1. взвешенного метода наименьших квадратов 2. метода максимального правдоподобия 3. метода инструментальных переменных 4. косвенного метода наименьших квадратов
Вопрос № 24.1. Оригинальный порядковый номер: 4 В приведенной форме модели в правой части уравнений находятся … Варианты ответов. Кол-во правильных ответов - 1 1. только зависимые переменные 2. только независимые переменные 3. случайные факторы 4. зависимые и независимые переменные Вопрос № 24.2. Оригинальный порядковый номер: 13 Для сверхидентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется ______ метод наименьших квадратов. Варианты ответов. Кол-во правильных ответов - 1 1. традиционный 2. двухшаговый 3. косвенный 4. трехшаговый Вопрос № 24.3. Оригинальный порядковый номер: 14 Приведена последовательность операций: 1. заданная система одновременных уравнений из структурной формы преобразуется в приведенную форму 2. оценки параметров приведенной формы находятся традиционным методом наименьших квадратов 3. по оценкам параметров приведенной формы вычисляются оценки структурных параметров. Этот алгоритм соответствует _____ методу наименьших квадратов. Варианты ответов. Кол-во правильных ответов - 1 1. косвенному 2. обобщенному 3. трехшаговому 4. двухшаговому Вопрос № 24.4. Оригинальный порядковый номер: 17 Приведена последовательность операций: 1. заданная система одновременных уравнений из структурной формы преобразуется в приведенную форму 2. оценки параметров приведенной формы находятся традиционным методом наименьших квадратов
3. определение расчетных значений эндогенных переменных, которые выступают в качестве факторов в структурной форме модели 4. определение структурных параметров каждого уравнения в отдельности традиционным методом наименьших квадратов, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на первом шаге. Этот алгоритм соответствует ____ методу наименьших квадратов. Варианты ответов. Кол-во правильных ответов - 1 1. косвенному 2. обобщенному 3. трехшаговому 4. двухшаговому Вопрос № 24.5. Оригинальный порядковый номер: 28 Оценки параметров идентифицируемой системы эконометрических уравнений могут быть найдены с помощью ______ метода наименьших квадратов. Варианты ответов. Кол-во правильных ответов - 1 1. взвешенного 2. косвенного 3. обобщенного 4. обычного
Начало формы
Конец формы
Вопрос №3 Уровень сложности - лёгкий (1 балл) Неправильно При построении модели тенденции в динамике уровня показателя уровни временного ряда рассматриваются как функции времени и периодических колебаний только времени --------только случайных колебаний времени и случайных колебаний Уровень сложности - средний (2 балла) Неправильно При использовании шагового регрессионного анализа при выборе наилучшей эконометрической регрессионной модели добавление нового фактора требует проверки значимости влияния на результат только нового фактора влияния на результат факторов, уже включенных в модель регрессии ---------только парных межфакторных коэффициентов корреляции только парных межфакторных коэффициентов детерминации Уровень сложности - средний (2 балла) Если коэффициент парной линейной корреляции равен 0.7, то доля вариации зависимого признака Y, объясняемой изменением факторного признака X, составляет
0,7% ++++49% = 0.7^2*100 0,3% 0,09% ----0,49% Вопрос №18 Уровень сложности - лёгкий (1 балл) Неправильно Автокорреляция уровней временного ряда – это корреляционная связь между последовательными значениями цепных и соответствующих базисных коэффициентов роста уровней ряда базисных абсолютных приростов уровней ряда -----цепных и соответствующих базисных абсолютных приростов уровней ряда уровней ряда Вопрос №19 Уровень сложности - лёгкий (1 балл) Нарушение условия независимости дисперсии остатков от номера наблюдения (непостоянство дисперсии) называют инвариантностью нестационарностью
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1011; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.119.71 (0.015 с.) |

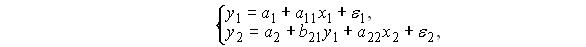 ошибка
ошибка  в уравнении для эндогенной переменной
в уравнении для эндогенной переменной 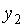 приведенной формы эконометрической модели
приведенной формы эконометрической модели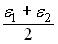

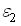
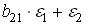

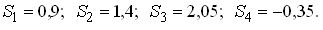



 –признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков
–признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков  и построено уравнение регрессии в стандартизованном масштабе
и построено уравнение регрессии в стандартизованном масштабе  Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:
Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:




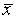 и
и  равны 1,2 и 3,6 соответственно, а коэффициент линейной корреляции равен 0,5, то параметр b в уравнении парной линейной регрессии
равны 1,2 и 3,6 соответственно, а коэффициент линейной корреляции равен 0,5, то параметр b в уравнении парной линейной регрессии  равен
равен , вычислены значения величин:
, вычислены значения величин: 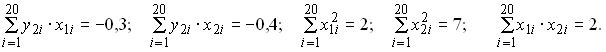 Тогда приведенное уравнение регрессии для эндогенной переменной
Тогда приведенное уравнение регрессии для эндогенной переменной  имеет вид:
имеет вид:


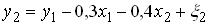
 по выборке объема n имеет вид:
по выборке объема n имеет вид:


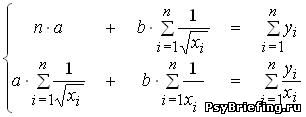
 . Индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение F -критерия равно 3,35. Построенная регрессионная модель значима, так как фактическое значение F -критерия равно
. Индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение F -критерия равно 3,35. Построенная регрессионная модель значима, так как фактическое значение F -критерия равно







 , – наблюдаемые значения признака-результата Y и факторного признака X соответственно, то параметры a,b уравнения парной линейной регрессии
, – наблюдаемые значения признака-результата Y и факторного признака X соответственно, то параметры a,b уравнения парной линейной регрессии  , можно определить как решение системы уравнений:
, можно определить как решение системы уравнений:

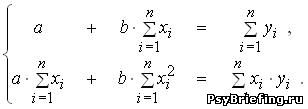
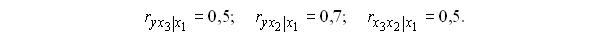 Тогда частный коэффициент линейной корреляции второго порядка
Тогда частный коэффициент линейной корреляции второго порядка  равен
равен



 Вычислены следующие значения сезонной составляющей:
Вычислены следующие значения сезонной составляющей:  Прогнозируемое значение показателя на 2-ой квартал 2010 года равно
Прогнозируемое значение показателя на 2-ой квартал 2010 года равно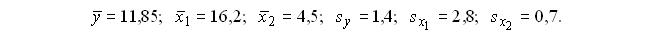 и построено уравнение регрессии в стандартизованном масштабе
и построено уравнение регрессии в стандартизованном масштабе  Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:
Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:
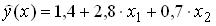




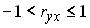

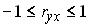
 Тогда частный коэффициент линейной корреляции второго порядка
Тогда частный коэффициент линейной корреляции второго порядка 

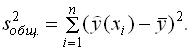
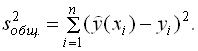
 и построено уравнение регрессии в стандартизованном масштабе
и построено уравнение регрессии в стандартизованном масштабе  Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:
Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле: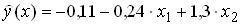



 коэффициент
коэффициент  при
при  во втором уравнении приведенной формы модели
во втором уравнении приведенной формы модели

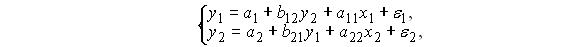

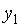 приведенной формы эконометрической модели
приведенной формы эконометрической модели

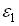
 и расчетные значения зависимой переменной y не коррелированны, то:
и расчетные значения зависимой переменной y не коррелированны, то:



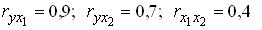 , то стандартизованные коэффициенты регрессии
, то стандартизованные коэффициенты регрессии  являются решением системы уравнений:
являются решением системы уравнений:








 следует преобразовать к виду:
следует преобразовать к виду: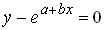
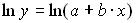


 множественной линейной регрессии, значим, если доверительный интервал, покрывающий этот параметр,
множественной линейной регрессии, значим, если доверительный интервал, покрывающий этот параметр,


