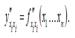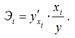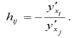Многофакторные производственные функции

Многофакторной производственной функцией называется функция, которая характеризует зависимость объёма производства от n -го количества факторов производства.

y=f(xi),

где

Многофакторные производственные функции полезны тем, что на их основе можно рассчитать целый ряд важнейших экономических показателей.

К основным показателям многофакторных производственных функций относятся:

1) показатель средней производительности (эффективности, отдачи) i -го фактора при условии фиксированности всех остальных факторов:

2) показатель предельной производительности (эффективности, отдачи) i -го фактора, который характеризует приращение объёма производства на единицу приращения i -го фактора, рассчитывается как частная производная по факторной переменной xi:

3) для определения характера изменения предельной производительности с изменением объёма i -го фактора при постоянном значении всех остальных факторов, включённых в модель, рассчитывается частная производная второго порядка по факторной переменной xi:

Если показатель

больше нуля, то предельная производительность возрастает с ростом объёма i-ой факторной переменной.

Если показатель

равен нулю, то можно найти такое значение объёма i-ой факторной переменной, при котором предельная производительность будет или минимальной или максимальной.

4) показатель частной эластичности i-го ресурса для многофакторной производственной функции характеризует относительное изменение результата производства на единицу относительного изменения i-ой факторной переменной:

5) потребность производства в i-том факторе выражается через функциональную зависимость вида:

xi=φ(y,x1…xi-1,xi+1…xn).

6) для любой пары факторов производства i и j можно рассчитать предельную норму замещения j-ой факторной переменной i-той факторной переменной. Эта норма равна взятому со знаком минус отношению показателей предельной производительности i-ой и j-ой факторных переменных:

При выборе конкретного вида производственной функции исследователь должен руководствоваться закономерностями изменения всех рассмотренных показателей. В некоторых случаях выбранную форму производственной функции приходится отвергать, потому что соответствующая ей система показателей противоречит результатам качественного анализа или эмпирическим данным. С другой стороны предварительные заключения о характере изменений рассмотренных показателей могут стать основным доводом в пользу выбора той или иной формы производственной функции.

Модели бинарного выбора

Результативная переменная у в нормальной линейной модели регрессии является непрерывной величиной, способной принимать любые значения из заданного множества. Но помимо нормальных линейных моделей регрессии существуют модели регрессии, в которых переменная у должна принимать определённый узкий круг заранее заданных значений.

Моделью бинарного выбора называется модель регрессии, в которой результативная переменная может принимать только узкий круг заранее заданных значений

В качестве примеров бинарных результативных переменных можно привести:

Приведенные в качестве примеров бинарные переменные являются дискретными величинами. Бинарная непрерывная величина задаётся следующим образом:

Если стоит задача построения модели регрессии, включающей результативную бинарную переменную, то прогнозные значения yiпрогноз, полученные с помощью данной модели, будут выходить за пределы интервала [ 0;+1 ] и не будут поддаваться интерпретации. В этом случае задача построения модели регрессии формулируется не как предсказание конкретных значений бинарной переменной, а как предсказание непрерывной переменной, значения которой заключаются в интервале [ 0;+1 ].

Решением данной задачи будет являться кривая, удовлетворяющая следующим трём свойствам:

1) 1) F(–∞)=0;

2) F(+∞)=1;

3) F(x1)>F(x2) при условии, что x1> x2.

Данным трём свойствам удовлетворяет функция распределения вероятности.

Модель парной регрессии с результативной бинарной переменной с помощью функции распределения вероятности можно представить в следующем виде:

prob(yi=1)=F(β0+β1xi),

где prob(yi=1) – это вероятность того, что результативная переменная yi примет значение, равное единице.

В этом случае прогнозные значения yiпрогноз, полученные с помощью данной модели, будут лежать в пределах интервала [ 0;+1 ].

Модель бинарного выбора может быть представлена с помощью скрытой или латентной переменной следующим образом:

Векторная форма модели бинарного выбора с латентной переменной:

В данном случае результативная бинарная переменная yi принимает значения в зависимости от латентной переменной yi*:

Модель бинарного выбора называется пробит-моделью или пробит-регрессией (probit regression), если она удовлетворяет двум условиям:

1) остатки модели бинарного выбора εi являются случайными нормально распределёнными величинами;

2) функция распределения вероятностей является нормальной вероятностной функцией.

Пробит-регрессия может быть представлена с помощью выражения:

NP(yi)=NP(β0+β1x1i+…+βkxki),

где NP – это нормальная вероятность (normal probability).

Модель бинарного выбора называется логит-моделью или логит-регрессией (logit regression), если случайные остатки εi подчиняются логистическому закону распределения.

Логит-регрессия может быть представлена с помощью выражения:

Данная модель логит-регрессии характеризуется тем, что при любых значениях факторных переменных и коэффициентов регрессии, значения результативной переменной yi будут всегда лежать в интервале [0;+1].

Обобщённый вид модели логит-регрессии:

Достоинством данной модели является то, что результативная переменная yi может произвольно меняться внутри заданного числового интервала (не только от нуля до плюс единицы).

Логит-регрессия относится к классу функций, которые можно привести к линейному виду. Это осуществляется с помощью преобразования, носящего название логистического или логит преобразования, которое можно проиллюстрировать на примере преобразования обычной вероятности р:

Качество построенной логит-регрессии или пробит-регрессии характеризуется с помощью псевдо коэффициента детерминации, который рассчитывается по формуле:

Если значение данного коэффициента близко к единице, то модель регрессии считается адекватной реальным данным.