Вопрос № 22.2. Оригинальный порядковый номер: 5

Система взаимозависимых уравнений в ее классическом виде называется также системой _______ уравнений.

Варианты ответов. Кол-во правильных ответов - 1

1. рекурсивных

2. изолированных

3. одновременных

4. независимых

Вопрос № 22.3. Оригинальный порядковый номер: 7

Выделяют три класса систем эконометрических уравнений: …

Варианты ответов. Кол-во правильных ответов - 1

1. системы независимых уравнений, системы изолированных уравнений и системы рекурсивных уравнений

2. системы взаимозависимых уравнения, системы рекурсивных уравнений и системы возвратных уравнений

3. системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений

4. системы одновременных уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений

Вопрос № 22.4. Оригинальный порядковый номер: 9

В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как _____ количества зависимых переменных ______ уравнений и количества независимых факторов.

Варианты ответов. Кол-во правильных ответов - 1

1. разность … предыдущих

2. разность … последующих

3. сумма … предыдущих

4. сумма … последующих

Вопрос № 22.5. Оригинальный порядковый номер: 21

Если структурная форма модели системы эконометрических уравнений точно идентифицируема, то с помощью косвенного МНК …

Варианты ответов. Кол-во правильных ответов - 1

1. нулевые значения параметров модели

2. оценки для параметров модели определить невозможно

3. получают единственную оценку параметров модели

4. получают несколько различных вариантов оценок параметров модели

 

Вопрос № 22.1. Оригинальный порядковый номер: 2

Левая часть системы взаимозависимых уравнений представлена вектором …

Варианты ответов. Кол-во правильных ответов - 1

1. зависимых переменных и случайных величин

2. зависимых независимых переменных

3. зависимых переменных

4. независимых переменных

Вопрос № 22.2. Оригинальный порядковый номер: 11

Система уравнений, в которых каждая эндогенная переменная рассматривается как функция только предопределенных переменных, называется системой _____ уравнений.

Варианты ответов. Кол-во правильных ответов - 1

1. одновременных

2. регрессионных

3. независимых

4. рекурсивных

Вопрос № 22.3. Оригинальный порядковый номер: 20

Система уравнений, где эндогенные переменные в одних уравнениях выступают в роли результирующего признака, а в других уравнениях – в роли фактора, называется системой ______ уравнений.

Варианты ответов. Кол-во правильных ответов - 1

1. независимых

2. изолированных

3. одновременных

4. рекурсивных

Вопрос № 22.4. Оригинальный порядковый номер: 25

Пусть D – число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, а H – число эндогенных переменных в уравнении. Уравнение системы считается неидентифицируемым, если …

Варианты ответов. Кол-во правильных ответов - 1

1.

2.

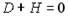
3.

4.

Вопрос № 22.5. Оригинальный порядковый номер: 27

Для оценки параметров структурной модели системы необходимо, чтобы …

Варианты ответов. Кол-во правильных ответов - 1

1. все уравнения системы были неидентифицируемы или сверхидентифицируемы

2. хотя бы одно уравнение системы было неидентифицируемо или сверхидентифицируемо

3. все уравнения системы были идентифицируемы или сверхидентифицируемы

4. хотя бы одно уравнение системы было идентифицируемо или сверхидентифицируемо

 

Вопрос № 22.1. Оригинальный порядковый номер: 3

Выберите верные утверждения по поводу системы независимых уравнений:

Варианты ответов. Кол-во правильных ответов - 2

1. каждое уравнение системы может рассматриваться в качестве отдельного уравнения регрессии зависимости одной переменной от группы факторов

2. каждая зависимая переменная рассматривается как функция только от предопределенных переменных

3. оценки параметров уравнений нельзя определить методом наименьших квадратов

4. каждая независимая переменная является функцией от всех других независимых переменных