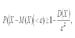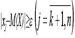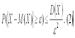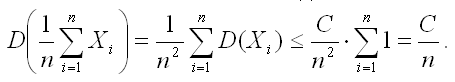Основные математические предпосылки эконометрического моделирования. Закон больших чисел, неравенство и теорема Чебышева

Основными математическими предпосылками эконометрического моделирования являются теоремы Чебышева, Бернулли и Ляпунова. Совокупность этих теорем носит общее название закона больших чисел.

На практике исследователи часто сталкиваются с таким комплексом условий, при осуществлении которого совокупное поведение достаточно большого количества случайных величин почти утрачивает случайный характер и приобретает определённые закономерности. Поэтому для решения подобных задач необходимо знать данный подобный комплекс условий, вследствие которого результат совокупного воздействия количества случайных факторов почти не зависит от случая. В этом случае опираются на закон больших чисел.

Для рассмотрения теоремы Чебышева вначале необходимо доказать неравенство Чебышева. Неравенство Чебышева справедливо как для дискретных, так непрерывных случайных величин. Рассмотрим его на примере дискретных случайных величин.

Предположим, что случайная дискретная величина X подчиняется закону распределения вида:

Задача состоит в оценке вероятности того, что отклонение случайной величины Х от её математического ожидания М(Х) не превышает по абсолютной величине положительного числа β. Если число β достаточно мало, то задача будет состоять в оценке вероятности того, что случайная величина Х примет значения, достаточно близкие к своему математическому ожиданию М(Х). Данная задача решается с применением неравенства П.Л. Чебышева.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от её математического ожидания М(Х) по абсолютной величине меньше положительного числа β не меньше, чем

т. е.

Доказательство. Так как события |Х-М(Х)|‹ε и |Х-М(Х)|≥ε являются противоположными, то на основании теоремы сложения вероятностей сумма их вероятностей равна единице:

P(|Х-М(Х)|‹ε)+P(|Х-М(Х)|≥ε)=1.

Выразим из полученного равенства вероятность | Х-М(Х)|‹ε:

P(|Х-М(Х)|‹ε)=1– P(|Х-М(Х)|≥ε). (1)

Дисперсия случайной величины Х определяется по формуле:

D(X)=(x1–M(X))2*p1+(x2–M(X))2*p2+…+(xn–M(X))2*pn.

Если отбросить первые k+1 слагаемые, для которых выполняется условие |xj-M(X)|‹ ε, то получим следующее неравенство:

D(X)≥(xk+1–M(X))2*pk+1+(xk+2–M(X))2*pk+2+…+(xn–M(X))2*pn.

Возведя обе части неравенства

в квадрат, получим равносильное неравенство |xj–M(X)|2≥ε2. Если заменить в оставшейся сумме каждый из множителей |xj–M(X)|2 числом β2, то получим следующее выражение:

D(X)≥ ε2(pk+1+ pk+2+…+ pn).

Так как сумма в скобках (pk+1+ pk+2+…+ pn) является выражением вероятности P(|Х-М(Х)|≥ε), то справедливо неравенство (2):

D(X)≥ ε2P(|Х-М(Х)|≥ε),

или

Если подставить неравенство (2) в выражение (1), то получим:

что и требовалось доказать.

Теорема Чебышева. Если величины X1, X2, …, Xn являются последовательностью попарно независимых случайных величин, имеющих дисперсии, ограниченные одной и той же постоянной С (D(Xi)≤C), то, как бы ни было мало положительное число ε, вероятность неравенства

ε будет приближаться к единице, если число случайных величин достаточно мало. Другими словами, для любого положительного числа существует предел:

Доказательство. В силу второго свойства дисперсии (постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат) и оценки D(Xi)≤C получим:

Таким образом,

Из данного соотношения и неравенства Чебышева вытекает, что

Отсюда, переходя к пределу при n›ε, получим

Учитывая, что вероятность не может быть больше единицы, окончательно запишем:

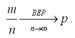
что и требовалось доказать.

Если для рассматриваемых случайных величин математическое ожидание одинаково и дисперсии данных величин ограничены, то к ним применима теорема Чебышева. В этом случае считается справедливым утверждение, что среднее арифметическое достаточно большого количества попарно независимых случайных величин, дисперсии которых ограничены одной и той же постоянной, утрачивает характер случайной величины.

Теоремы Бернулли и Ляпунова

Предположим, что проводится n независимых испытаний. В каждом из этих испытаний вероятность наступления события А постоянна и равна р. Задача состоит в определении относительной частоты появлений события А. Данная задача решается с помощью теоремы Бернулли.

Теорема Бернулли. Если в каждом из n независимых испытаний событие A имеет постоянную вероятность p, то, как угодно близка к единице вероятность того, что отклонение относительной частоты m/n от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, т. е. при соблюдении условий теоремы справедливо равенство:

Доказательство. Предположим, что

является дискретной случайной величиной, которая характеризует число появлений события А в каждом из испытаний. Данная величина может принимать только два значения: 1 (событие А наступило) с вероятностью р и 0 (событие А не наступило) с вероятностью q=1-p.

Случайные дискретные величины Хi являются попарно независимыми и дисперсии их ограниченны, следовательно, к данным величинам применима теорема Чебышева:

Математическое ожидание а каждой из величин Хi равно вероятности р наступления события, следовательно, справедливо следующее равенство:

Таким образом, необходимо доказать, что дробь

или

равна относительной частоте m/n появлений события А в n испытаниях.

Каждая из величин

при наступлении события А в соответствующем испытании принимает значение, равное единице. Следовательс

равна числу m появлений события А в n испытаниях:

С учётом данного равенства можно окончательно записать:

что и требовалось доказать.

Однако при использовании теоремы Бернулли необходимо учитывать то, что из неё не следует равенство

Главным утверждением теоремы является то, что при достаточно большом количестве испытаний относительная частота m/n будет сколь угодно мало отличаться от постоянной вероятности р наступления события в каждом испытании. Другими словами, теорема Бернулли утверждает, что при n› ε относительная частота стремится по вероятности к р. Поэтому теорема Бернулли может быть записана следующим образом:

При проведении статистических исследований, в ходе которых осуществляется сбор данных об исследуемом объекте или процессе, часто сталкиваются с проблемой ошибочности наблюдений. В основе ошибочности наблюдений может лежать как несовершенство методов и инструментов, используемых при проведении статистического исследования, так и заранее непредусмотренные факторы. В связи с этим возникла задача исключения подобных ошибок наблюдения.

Ошибки наблюдения делятся на систематические ошибки и случайные ошибки.

Систематическими ошибками наблюдения называются такие ошибки, которые вызваны несовершенством методов и инструментов, применяемых при проведении исследования. Теоретически все систематические ошибки наблюдения могут быть исключены.

Случайными ошибками наблюдения называются такие ошибки, которые возникают под воздействием целой совокупности случайных факторов. При этом каждый из этих факторов в отдельности вызывает частичную ошибку, а результатом совместного действия всех случайных факторов является суммарная случайная ошибка, которую уже подлежит оценке.

Допустим, что была проведена серия наблюдений некоторой случайной величины Х. В ходе наблюдений данной случайной величины возникли ошибки, сформированные воздействием множества независимых факторов

Тогда ошибка а, возникающая в ходе наблюдения случайной величины Х, может быть представлена с помощью выражения:

а=f(X1,X2,…,Xn),

где f – это закономерность образования ошибки.

В связи с тем, что ошибка наблюдений а – величина случайная, то для наиболее точной характеристики данной величины необходимо знать закон распределения её вероятностей. Данная задача решается с помощью теоремы А.М. Ляпунова, также известной под названием центральной предельной теоремы. В качестве одной из математических предпосылок эконометрического моделирования выступает следствие из теоремы Ляпунова.

Следствие теоремы Ляпунова. Если случайная величина Х является суммой очень большого числа попарно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то случайная величина Х подчиняется закону распределения, который близок к нормальному закону распределения вероятностей случайной величины.

Если суммарную ошибку наблюдений рассматривать как сумму очень большого числа попарно независимых частных ошибок, следовательно, то можно сделать вывод, что суммарная ошибка подчиняется закону распределения, который близок к нормальному закону распределения вероятностей.