
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон больших чисел Чебышева.Содержание книги
Поиск на нашем сайте Имеет место следующее утверждение. Пусть
Закон больших чисел Бернулли. Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):
21. Неравенство Чебышева. неравенство Чебышева. Пусть Х – неотрицательная случайная величина (т.е.
Доказательство. Все слагаемые в правой части формулы
Для всех слагаемых в правой части (9)
Из (9) и (10) следует требуемое.
22. Теорема Чебышева. Теорема Чебышева Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается: Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины. Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий. Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются. Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности. 23. Следствие из теоремы Чебышева. Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико. Следствие. Если независимые случайные величины имеют одинаковые, равные a, математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е. При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:
24. Закон больших чисел в форме Бернулли. (ЗБЧ Бернулли). Пусть событие
Доказательство. Заметим, что
и Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством 25. Случайные векторы. Совместный закон распределения двух случайных величин. Горох!)))
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 940; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.
- последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.  для любого i. Тогда, каково бы нибыло
для любого i. Тогда, каково бы нибыло  , справедливо соотношение
, справедливо соотношение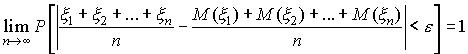


 для любого
для любого  ). Тогда для любого положительного числа а справедливо неравенство
). Тогда для любого положительного числа а справедливо неравенство
 определяющей математическое ожидание, в рассматриваемом случае неотрицательны. Поэтому при отбрасывании некоторых слагаемых сумма не увеличивается. Оставим в сумме только те члены, для которых
определяющей математическое ожидание, в рассматриваемом случае неотрицательны. Поэтому при отбрасывании некоторых слагаемых сумма не увеличивается. Оставим в сумме только те члены, для которых 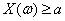 . Получим, что
. Получим, что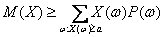 . (9)
. (9)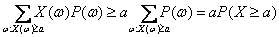 . (10)
. (10) , (63)
, (63)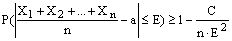
 может произойти в любом из
может произойти в любом из 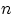 независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью 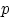 , и пусть
, и пусть  — число осуществлений события
— число осуществлений события  . При этом для любого
. При этом для любого 

 (индикаторовтого, что в соответствующем испытании произошло
(индикаторовтого, что в соответствующем испытании произошло  , где
, где
 ,
, 
 .
.


