
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенство и теорема ЧебышеваСодержание книги
Поиск на нашем сайте
Неравенство Чебышева. Вероятность того, что отклонение случайной величины от ее математического ожидания по модулю меньше числа Рассмотрим дискретную случайную величину X, имеющую закон распределения:
Закон распределения случайной величины
Предположим, что первые k значений случайной величины Теорема Чебышева. Если Рассмотрим случайную величину
Теорема Бернулли Пусть в каждом из n независимых испытаний вероятность p появления события А постоянна. Тогда как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Или Пусть Теорема Пуассона. Если в последовательности n независимых испытаний вероятность появления события А в каждом испытании равна Пусть случайная величина
Функция одного случайного аргумента и ее распределение
Если каждому возможному значения случайной величины Х соответствует одно возможное значение случайной величины Y, то Y – функция от X: Y=j(X). Найдем закон распределения вероятностей функции по известному распределению дискретного и непрерывного аргумента. 1) Если X – дискретная величина. Найти распределение Y=X2. Вероятности соответствующих значений X и Y равны:
2) Пусть X – непрерывная случайная величина. Пусть Y=j(X) и плотность распределения f(x) известна, тогда
Математическое ожидание функции одного случайного аргумента
Пусть Y=j (X) – функция случайного аргумента Х. Найдем M (Y). Пусть Х дискретная случайная величина: Пусть X – непрерывная случайная величина, заданная плотностью f (x). а) можно найти g (y) – плотность распределения величины Y и
Закон распределения вероятностей и функция распределения двумерных случайных величин
До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом – одномерные. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются 2, 3,…, n числами. Такие величины называются двумерными, трехмерными, …, n -мерными. Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X, Y называют компонентами (составляющими); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Пример: станок штампует плитки. Если контролировать длину X и ширину Y – то имеем двухмерную случайную величину (X, Y).
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.114 (0.009 с.) |

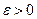 , не меньше, чем
, не меньше, чем 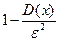 , т.е.
, т.е. 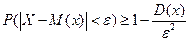 .
.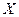

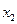

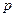
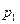

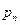
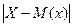 :
: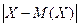
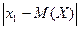
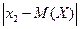
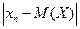
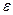 . Тогда
. Тогда 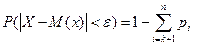 . Запишем формулу для дисперсии в виде:
. Запишем формулу для дисперсии в виде: 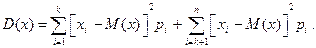 Отбросим первое слагаемое и во втором слагаемом заменим
Отбросим первое слагаемое и во втором слагаемом заменим 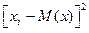 меньшей величиной
меньшей величиной 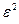 , получим
, получим 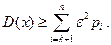 Отсюда:
Отсюда: 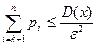 , т.е.
, т.е. 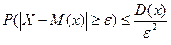 . Для частости:
. Для частости:  .
.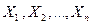 - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было
- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было 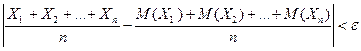 будет как угодно близка к единице, если число случайных величин достаточно велико, т.е.
будет как угодно близка к единице, если число случайных величин достаточно велико, т.е. 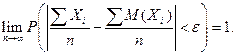
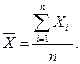 Имеем:
Имеем: 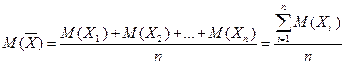 ;
; 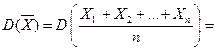
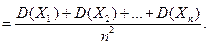 По условию теоремы дисперсия ограничена, т.е.
По условию теоремы дисперсия ограничена, т.е. 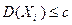 , поэтому
, поэтому 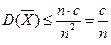 . Воспользуемся неравенством Чебышева:
. Воспользуемся неравенством Чебышева: 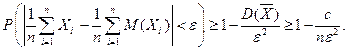 Перейдя к пределу и учитывая, что
Перейдя к пределу и учитывая, что 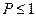 , получим доказываемое.
, получим доказываемое. , где
, где 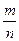 – частота появления события A.
– частота появления события A.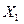 – число появлений события A в первом испытании,
– число появлений события A в первом испытании, 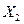 – во втором,
– во втором,  – в n -ом испытании,
– в n -ом испытании, 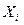 может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью
может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью 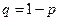 . Испытания независимые,
. Испытания независимые, 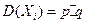 , так как
, так как 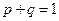 , то
, то 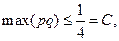
 , тогда по неравенству Чебышева:
, тогда по неравенству Чебышева: 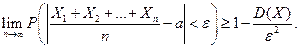
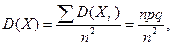
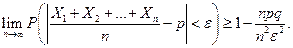 Каждая величина
Каждая величина 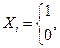 тогда
тогда 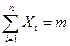 – числу появления события А в n испытаниях, тогда
– числу появления события А в n испытаниях, тогда 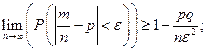 следовательно,
следовательно, 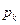 , то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей
, то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей 
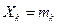 – число появлений события А в каждом испытании, тогда
– число появлений события А в каждом испытании, тогда 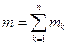 – число появлений события А в n испытаниях.
– число появлений события А в n испытаниях. 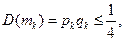
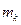 – независимые величины. Для случайной величины
– независимые величины. Для случайной величины 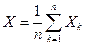 имеем:
имеем: 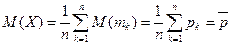 среднее арифметическое вероятностей;
среднее арифметическое вероятностей; 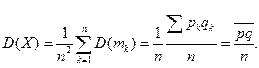 Тогда по неравенству Чебышева:
Тогда по неравенству Чебышева: 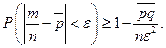 Переходя к пределу, получим доказываемое.
Переходя к пределу, получим доказываемое.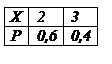
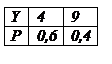
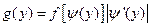 , где
, где 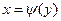 – обратная функция для функции у=j (х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.
– обратная функция для функции у=j (х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.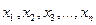 с вероятностью
с вероятностью 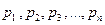 , Y – тоже дискретная случайная величина со значениями:
, Y – тоже дискретная случайная величина со значениями: 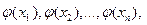 с вероятностью
с вероятностью 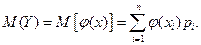
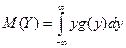 , однако проще:
, однако проще: 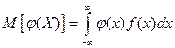 .
.


