
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностный смысл математического ожиданияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть проведено n испытаний, в которых случайная величина Х приняла
Допустим, что число испытаний достаточно велико, тогда Таким образом, математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства М (Х) 1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М (С) = С, С = const. С имеет одно значение, равное С,с вероятностью p = 1, М (С) =С . 1 = С. Определим произведение постоянной С на Х как дискретную случайную величину 2. М (СХ) = С . М (Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величина X задана законом распределения:
Тогда
Случайные величины X и Y называют независимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая. Произведение 3. Пусть законы распределения вероятностей этих величин:
Составим значения, которые могут принимать
4. M (X+Y) = M (X) + M (Y). Возможные значения случайной величины X + Y равна сумме возможных значений X и Y, а вероятность X+Y равна произведению вероятностей слагаемых. Теорема. М (Х) числа появлений событий А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытании p. Иначе, М (Х) биноминального распределения равно
Дисперсия случайной дискретной величины и ее свойства Легко указать случайные величины, имеющие одинаковые значения математических ожиданий, но различные возможные значения, например:
Х имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от М (Y), таким образом, М (Х) полностью не характеризует Х. Надо охарактеризовать отклонение случайной величины от M (X): отклонение – это величина X – M (X). Теорема. Математическое ожидание отклонения равно нулю. Действительно, Дисперсией (рассеянием) дискретных случайных величин называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: Получаем: Пример. Найти
M (X) = 1 . 0,3 + 2 . 0,5 + 5 . 0,2 = 2,3. Найдем все возможные значения квадрата отклонения: Напишем закон распределения квадрата отклонения:
Тогда (по определению): Удобнее: Доказательство:
Вычислим дисперсию в предыдущем примере по доказанной формуле. Составим закон распределения
Тогда
Свойства дисперсии 1. Дисперсия постоянной величины равной нулю. D (C) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Если |C| > 1, то величина СХ имеет большие (по модулю) значения, поэтому D (CX)> D (X). 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D (X+Y) = D (X) + D (Y). Докажем:
Следствие: D (X+C) = D (X) + D (C) = D (X), С = const. 4. D (X – Y) = D (X) + D (Y). Докажем: D (X–Y) = D (X) + D (–Y) = D (X) + (–1)2 D (X) = = D (X) + D (Y). Теорема. Дисперсия числа появлений событий А в n независимых испытаниях, в каждом из которых вероятность появления события А p = const, равна npq = D (X),где Иначе. Дисперсия биноминального распределения равна D (X)= npq.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.34.93 (0.008 с.) |

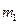 раз значение
раз значение  ,
, 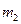 раз значение
раз значение 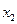 , …,
, …, 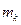 раз –
раз – 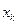 ,
, 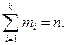 Тогда сумма всех значений, принятых Х равна
Тогда сумма всех значений, принятых Х равна 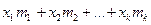 . Найдем среднее арифметическое
. Найдем среднее арифметическое 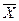 всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний n:
всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний n: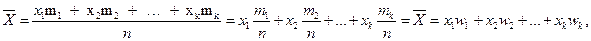 где
где 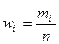 - относительная частота (частость).
- относительная частота (частость).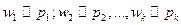 и
и 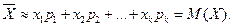
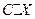 , возможные значения которой равны произведениям С на возможные значения Х. Вероятность
, возможные значения которой равны произведениям С на возможные значения Х. Вероятность 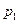 , то
, то 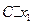 имеет также вероятность
имеет также вероятность 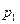 .
.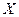

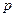
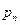

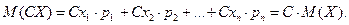
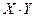 – случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y.
– случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y.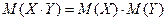 , где X, Y – независимые дискретные случайные величины.
, где X, Y – независимые дискретные случайные величины.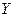
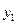
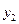


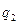
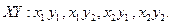 Закон распределения:
Закон распределения:
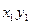
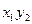
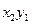

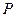
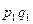



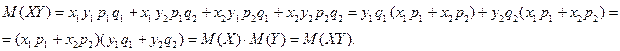
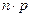 .
.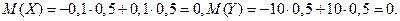
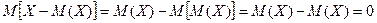 , поэтому для оценки отклонения берут квадрат отклонения.
, поэтому для оценки отклонения берут квадрат отклонения.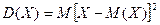 .
.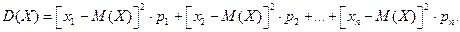
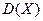 случайной величины:
случайной величины: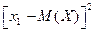 = (1 – 2,3)2 = 1,69;
= (1 – 2,3)2 = 1,69; 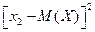 = (2 – 2,3)2 = 0,09;
= (2 – 2,3)2 = 0,09; 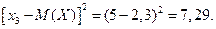

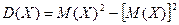 .
.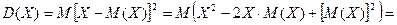
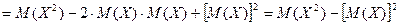 .
.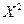 :
: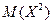 = 1 . 0,3 + 4 . 0,5 + 25 . 0,2 = 7,3. Найдем
= 1 . 0,3 + 4 . 0,5 + 25 . 0,2 = 7,3. Найдем 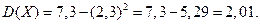
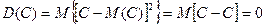 .
.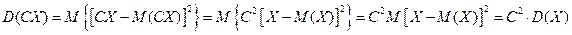 .
.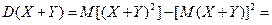
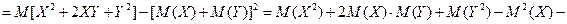

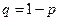 .
.


