
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение выборочной средней с математическим ожиданиемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него. Определение Пусть
Свойства выборочного среднего Пусть F(x) — выборочная функция распределения данной выборки. Тогда для любого фиксированного
Выборочное среднее — сильно состоятельная оценка теоретического среднего:
по распределению при Выборочное среднее из нормальной выборки — эффективная оценка её среднего. Математи́ческое ожида́ние — мера среднего значения случайной величины в теории вероятностей. В англоязычной литературе и в математическом сообществе Санкт-Петербурга обозначается через E[X](например, от англ. Expected value или нем. Erwartungswert), в русской — M[X] (возможно, от англ. Mean value, а возможно от русск. Математическое ожидание). В статистике часто используют обозначение м. Определение Пусть задано вероятностное пространство Основные формулы для математического ожидания Если FX(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:
Математическое ожидание дискретного распределения Если X — дискретная случайная величина, имеющая распределение Если X — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
то её математическое ожидание может быть выражено через производящую функцию последовательности {pi} Теперь возьмём производящую функцию Q(s) последовательности «хвостов» распределения {qk} Эта производящая функция связана с определённой ранее функцией P(s) свойством: M[X] = P'(1) = Q(1) Математическое ожидание абсолютно непрерывного распределения Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью fX(x), равно Пусть Математическое ожидание преобразования случайной величины Пусть
если X имеет дискретное распределение;
если X имеет абсолютно непрерывное распределение. Если распределение Pxслучайной величины X общего вида, то Простейшие свойства математического ожидания Математическое ожидание числа есть само число. M[a] = a Математическое ожидание линейно, то есть M[aX + bY] = aM[X] + bM[Y], где X,Y — случайные величины с конечным математическим ожиданием, а Математическое ожидание сохраняет неравенства, то есть если
Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если X = Y почти наверное, то M[X] = M[Y]. Математическое ожидание произведения двух независимых случайных величин X,Y равно произведению их математических ожиданий M[XY] = M[X]M[Y].
Вопрос 24.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.238.1 (0.006 с.) |

 — выборка из распределения вероятности, определённая на некотором вероятностном пространстве
— выборка из распределения вероятности, определённая на некотором вероятностном пространстве  . Тогда её выборочным средним называется случайная величина
. Тогда её выборочным средним называется случайная величина
 функция F(w;x) является (неслучайной) функцией дискретного распределения. Тогда математическое ожидание этого распределения равно X(w). Выборочное среднее — несмещённая оценка теоретического среднего:
функция F(w;x) является (неслучайной) функцией дискретного распределения. Тогда математическое ожидание этого распределения равно X(w). Выборочное среднее — несмещённая оценка теоретического среднего:
 почти наверное при
почти наверное при  . Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин Xi конечна и ненулевая, то есть
. Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин Xi конечна и ненулевая, то есть  . Тогда
. Тогда
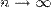 , где N(0,у2) — нормальное распределение со средним 0 и дисперсией у2.
, где N(0,у2) — нормальное распределение со средним 0 и дисперсией у2. и определённая на нём случайная величина X. То есть, по определению,
и определённая на нём случайная величина X. То есть, по определению,  — измеримая функция. Если существует интеграл Лебега от X по пространству Щ, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или E[X].
— измеримая функция. Если существует интеграл Лебега от X по пространству Щ, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или E[X]. 
 .
. , то прямо из определения интеграла Лебега следует, что
, то прямо из определения интеграла Лебега следует, что  . Математическое ожидание целочисленной величины
. Математическое ожидание целочисленной величины
 как значение первой производной в единице: M[X] = P'(1). Если математическое ожидание X бесконечно, то
как значение первой производной в единице: M[X] = P'(1). Если математическое ожидание X бесконечно, то  и мы будем писать
и мы будем писать 

 при | s | < 1. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
при | s | < 1. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице: . Математическое ожидание случайного вектора
. Математическое ожидание случайного вектора — случайный вектор. Тогда по определению
— случайный вектор. Тогда по определению  , то есть математическое ожидание вектора определяется покомпонентно.
, то есть математическое ожидание вектора определяется покомпонентно.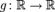 — борелевская функция, такая что случайная величина Y = g(X) имеет конечное математическое ожидание. Тогда для него справедлива формула:
— борелевская функция, такая что случайная величина Y = g(X) имеет конечное математическое ожидание. Тогда для него справедлива формула: ,
, ,
, . В специальном случае, когда g(X) = Xk, Математическое ожидание
. В специальном случае, когда g(X) = Xk, Математическое ожидание  называется k-тым моментом случайной величины.
называется k-тым моментом случайной величины. — константа;
— константа; — произвольные константы;
— произвольные константы; почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того
почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того ;
;


