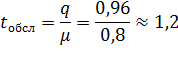Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение функции распределения длительности ожиданияСодержание книги
Поиск на нашем сайте
Если в момент поступления требования в очереди уже находились k-m требований, то, поскольку обслуживание происходит в порядке очередности, вновь поступившее требование должно ожидать, когда будут обслужены k-m+ 1 требований. Пусть
Так как распределение длительности обслуживания предположено показательным и не зависящим ни от того, сколько требований находится в очереди, ни от того, как велики длительности обслуживания других требований, то вероятность за время t не завершить ни одного обслуживания (т.е. вероятность того, что не освободится ни один из приборов) равна
Если все приборы заняты обслуживанием и ещё имеется достаточная очередь требований, которые ожидают обслуживания, то поток обслуженных требований будет простейшим. Действительно, в этом случае все три условия – стационарность, отсутствие последействия и ординарность – выполнены. Вероятность освобождения за промежуток времени t ровно s приборов равна (это можно показать и простым подсчетом)
Итак,
и, следовательно,
Но вероятности
поэтому
Очевидными преобразованиями приводим правую часть последнего равенства к виду
Из формул (18) и (19) следует, что
Само собой разумеется, что при t<0
Функция
Средняя длительность ожидания
Формула (22) позволяет находить все интересующие числовые характеристики длительности ожидания. В частности, математическое ожидание длительности ожидания начала обслуживания или, как предпочитают говорить, средняя длительность ожидания равна
Несложные вычисления приводят к формуле
Дисперсия величины
Формула (23) даёт среднюю длительность ожидания одного требования. Найдем среднюю потерю времени требованиями, пришедшими в систему обслуживания в течение промежутка времени T. За время T в систему поступает
Приведем небольшие арифметические подсчеты, которые продемонстрируют нам, как быстро возрастают суммарные потери времени па ожидание с изменением величины При т =1 в силу (20)
При р=0,1; 0,4; 0,6; 0,9 значение а При m=2 в силу (24)
При Приведённые данные иллюстрируют хорошо известный факт относительно большой чувствительности систем обслуживания, уже достаточно сильно загруженных, к возрастанию загрузки. Потребитель при этом сразу ощущает значительное возрастание длительности ожидания. Этот факт обязательно следует учитывать при расчёте загрузки оборудования в системах массового обслуживания. Пример практического решения задачи
Автозаправочная станция представляет собой СМО с 2 каналами обслуживания (двумя колонками). Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m=3). Если в очереди уже находятся три машины, очередная машина прибывшая к станции, в очередь не становится. Поток машин, прибывший для заправки, имеет интенсивность λ=1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин. Определить: · Вероятность отказа · Относительную и абсолютную пропускную способности АЗС · Среднее число машин, ожидающих заправки · Среднее число машин находящихся на АЗС (включая обслуживаемые) · Среднее время ожидание машины в очереди · Среднее время пребывания машины на АЗС (включая обслуживание) Решение: Находим вначале приведенную интенсивность потока заявок:
Вероятность отказа
Относительная пропускная способность СМО
Абсолютная пропускная способность СМО
Среднее число машин, ожидающих в очереди
т.е. среднее число машин, ожидающих в очереди на заправку равно 0,565 Прибавляя к этой величине среднее число машин, находящихся под обслуживанием
Получаем среднее число машин связанных с АЗС
Среднее время ожидания машины в очереди
Прибавляем к этой величине
Получим среднее время, которое машина проводит на АЗС
Заключение
В этой контрольной работе раскрыты понятия приводящие к системе массового обслуживания, а именно: обслуживание, обслуживает прибор система обслуживания, система массового обслуживания. Также описаны типичные элементы, из которых состоят системы массового обслуживания (входящий поток, его описание и основные особенности, очередь и ее дисциплина, обслуживающие приборы и особенности механизма обслуживания, входящий поток). Что касается практического задания, то рассмотренное данной задачей автозаправочная станция является СМО с ожиданием. На её примере я определил: вероятность отказа, относительную и абсолютную пропускную способности АЗС, среднее число машин, ожидающих заправки, среднее число машин находящихся на АЗС (включая обслуживаемые), среднее время ожидание машины в очереди, среднее время пребывания машины на АЗС (включая обслуживание). Список используемой литературы 1. Е.В. Бережная, В.И. Бережной. Математические методы моделирования экономических систем: Учеб. пособие. – М.: Финансы и статистика, 2001. 2. Математическое моделирование систем связи: учебное пособие / К.К. Васильев, М.Н. Служивый. – Ульяновск: УлГТУ, 2008. – 170 с. Размещено на Allbest.ru
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.254 (0.011 с.) |

 означает вероятность того, что за промежуток времени длительности t после поступления интересующего требования закончилось обслуживание ровно s требований. Ясно, что при
означает вероятность того, что за промежуток времени длительности t после поступления интересующего требования закончилось обслуживание ровно s требований. Ясно, что при  имеет место равенство
имеет место равенство




 известны:
известны:


 =
=

 .
. поэтому при m>0
поэтому при m>0 (22)
(22)
 имеет в точке t=1 разрыв непрерывности, равный вероятности застать все приборы занятыми.
имеет в точке t=1 разрыв непрерывности, равный вероятности застать все приборы занятыми.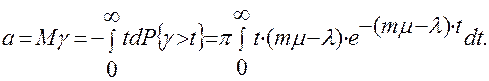
 (23)
(23) равна
равна
 требований и среднем; общая потеря ими времени па ожидание в среднем равна
требований и среднем; общая потеря ими времени па ожидание в среднем равна (24)
(24) . При этом мы ограничиваемся случаем Т=1 и рассматриваем лишь самые малые значения т: т =1 и т=2.
. При этом мы ограничиваемся случаем Т=1 и рассматриваем лишь самые малые значения т: т =1 и т=2.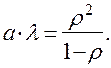
 приблизительно равно 0,011; 0,267; 0,9; 8,100.
приблизительно равно 0,011; 0,267; 0,9; 8,100.