
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процесс обслуживания как марковский случайный процессСодержание книги
Поиск на нашем сайте
В указанных нами предположениях о потоке требований и о длительности обслуживания задачи теории массового обслуживания приобретают некоторые черты, облегчающие проведение исследований. Мы отмечали уже вычислительную простоту. Теперь отметим более принципиальное соображение, которое станем развивать применительно к изучаемой задаче. В каждый момент рассматриваемая система может находиться в одном из следующих состоянии: в момент t в системе находятся k требовании (k=0, 1, 2,…). Если k Сформулируем, в чем заключается особенность изучаемых нами задач в сделанных предположениях. Пусть в некоторый момент моментами окончания обслуживаний, производящихся в момент моментами появления новых требований; длительностью обслуживания требований, поступивших после В силу особенностей показательного распределения длительность остающейся части обслуживания не зависит от того, как долго уже продолжалось обслуживание до момента Известно, что случайные процессы, для которых будущее развитие зависит только от достигнутого в данный момент состояния и не зависит от того, как происходило развитие в прошлом, называются процессами Маркова или же процессами без последействия. Итак, система с ожиданием в случае простейшего потока и показательного времени обслуживания представляет собой случайный процесс Маркова. Это обстоятельство облегчает дальнейшие рассуждении.
Составление уравнений
Задача теперь состоит в том, чтобы найти те уравнения, которым удовлетворяют вероятности
Найдём сначала вероятность того, что и момент t +h все приборы свободны. Это может произойти следующими способами: · в момент t все приборы были свободны и за время h новых требований не поступало; · в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило. Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них была закончена – имеют вероятность о(h), как легко в этом убедится. Вероятность первого из указанных событий равна
вероятность второго события
Таким образом
Отсюда очевидным образом приходим уравнению Перейдём теперь к составлению уравнений для В момент t система находилась в состоянии
В момент t система находилась в состоянии
В момент t система находилась в состоянии
Все остальные мыслимые возможности перехода в состояние Собрав воедино найденные вероятности, получаем следующее равенство:
Несложные преобразования приводят от этого равенства к такому уравнению для 1
Подобные же рассуждения для
Для определения вероятностей
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.239.38 (0.008 с.) |

 rn, то в системе находятся и обслуживаются k требований, а m-k – приборов свободны. Если k
rn, то в системе находятся и обслуживаются k требований, а m-k – приборов свободны. Если k 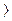 m, то m требований обслуживаются, а k-m находятся в очереди и ожидают обслуживания. Обозначим через
m, то m требований обслуживаются, а k-m находятся в очереди и ожидают обслуживания. Обозначим через  состояние, когда в системе находятся k требований. Таким образом, система может находиться в состояниях
состояние, когда в системе находятся k требований. Таким образом, система может находиться в состояниях  … Обозначим через
… Обозначим через  – вероятность того, что система в момент t окажется в состоянии
– вероятность того, что система в момент t окажется в состоянии  .
. наша система находилась и состоянии
наша система находилась и состоянии 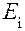 . Докажем, что последующее течение процесса обслуживания не зависит в смысле теории вероятностей от того, что происходило до момента
. Докажем, что последующее течение процесса обслуживания не зависит в смысле теории вероятностей от того, что происходило до момента  . Одно из уравнения очевидно, a именно для каждого t
. Одно из уравнения очевидно, a именно для каждого t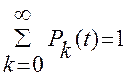 (2)
(2) ,
, .
. .
.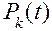 при
при  1. Рассмотрим отдельно два различных случая: 1
1. Рассмотрим отдельно два различных случая: 1  и
и  . Пусть в начале 1
. Пусть в начале 1 
 , за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна
, за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна
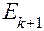 , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна
, за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна

 (4)
(4)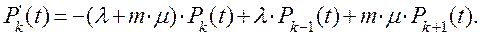 (5)
(5)


