
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая проверка статистических гипотезСодержание книги
Поиск на нашем сайте
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Нулевой (основной) называют выдвинутую гипотезу Конкурирующей называют гипотезу Н 1, которая противоречит нулевой. Если выдвинутая гипотеза будет отвергнута, то имеет место конкурирующая гипотеза. Выдвинутая гипотеза может быть правильной или неправильной, т.е. ее необходимо проверять. В итоге статистической проверки гипотез в двух случаях может быть принято неправильное решение: - ошибка 1 рода – будет отвергнута правильная гипотеза; - ошибка 2 рода – будет принята неправильная гипотеза. Для проверки статистической гипотезы используют статистический критерий, т.е. правило, устанавливающее условия, при которых проверяемую гипотезу следует либо принять, либо отвергнуть. Основу критерия составляет специальная случайная величина (статистика) K с известным законом распределения. Задаваясь уровнем значимости Основной принцип проверки гипотезы: если значение статистики, рассчитанное для выборки, попадает в критическую область, то гипотезу отвергают, в противном случае – гипотезу принимают. В зависимости от вида конкурирующей гипотезы Н 1выбирают: 1. правостороннюю критическую область 2. левостороннюю критическую область: 3. двухсторонняя критическая область:
Схема проверки гипотез 1. По условию задачи формулируют основную 2. Задают величину уровня значимости a: 0,05; 0,01; 0,001. 3. Выбирают статистику, определяющую критерии проверки и выясняют ее закон распределения. 4. С помощью закона распределения статистики определяют 5. По результатам выборки вычисляют значение статистики
24.2. Проверка гипотезы о равенстве двух дисперсий нормальных генеральных совокупностей Этот вопрос возникает, если требуется сравнить точности приборов, методов измерений и т.д. Пусть Х и Y – нормально распределенные генеральные совокупности. По двум выборкам объемами n 1 и n 2 найдены исправленные выборочные дисперсии Исправленные выборочные дисперсии обычно различные. Требуется установить: различие значимо (существенно) или незначимо, т.е. объясняется случайными причинами. Выбираем F – статистику, распределенную по закону Фишера–Снедекора. Наблюдаемое значение: Если Н1 : Иногда требуется проверить нулевую гипотезу а) Если конкурирующая гипотеза имеет вид б) если в) Если
Пример. По 2 выборкам объемами n 1 = 10 и n 2 = 18 найдены исправленные выборочные дисперсии Находим
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.4 (0.009 с.) |

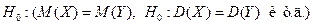 .
.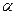 , т.е. вероятностью совершить ошибку 1 рода, критерий позволяет разбить все множество значений статистики на 2 непересекающихся подмножества: область принятия гипотезы и критическую область (область отклонения гипотезы).
, т.е. вероятностью совершить ошибку 1 рода, критерий позволяет разбить все множество значений статистики на 2 непересекающихся подмножества: область принятия гипотезы и критическую область (область отклонения гипотезы).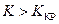 . Критическое значение статистики
. Критическое значение статистики 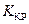 вычисляем из условия
вычисляем из условия 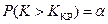 .
.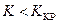 ,
, 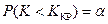 .
.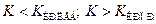 Обычно считают, что
Обычно считают, что 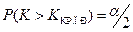 ,
, 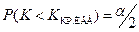 и если критические точки симметричны относительно нуля, то
и если критические точки симметричны относительно нуля, то  .
.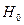 и конкурирующую гипотезы.
и конкурирующую гипотезы.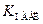 . Если
. Если 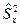 и
и 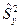 . При уровне значимости a проверяем нулевую гипотезу
. При уровне значимости a проверяем нулевую гипотезу 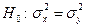 ,
, 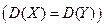 при конкурирующей гипотезе
при конкурирующей гипотезе  .
.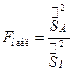 (отношение большой исправленной дисперсии к меньшей), число степеней свободы:
(отношение большой исправленной дисперсии к меньшей), число степеней свободы: 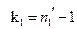 (где
(где 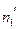 - объем выборки с большей исправленной дисперсией),
- объем выборки с большей исправленной дисперсией), 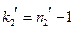 (где
(где 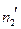 - объем выборки с меньшей исправленной дисперсией). По таблице критических точек распределения Фишера–Снедекора для уровня значимости a, числа степеней свободы
- объем выборки с меньшей исправленной дисперсией). По таблице критических точек распределения Фишера–Снедекора для уровня значимости a, числа степеней свободы  определяем
определяем 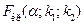 . Если
. Если 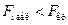 , то гипотеза принимается, если
, то гипотеза принимается, если 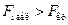 , то гипотеза отвергается.
, то гипотеза отвергается. , то значение
, то значение 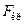 определяется для уровня значимости
определяется для уровня значимости 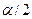 , поскольку необходимо построить двухстороннюю критическую область
, поскольку необходимо построить двухстороннюю критическую область  и
и  .
. – определенное заданное значение генеральной дисперсии. Для проверки используют статистику
– определенное заданное значение генеральной дисперсии. Для проверки используют статистику 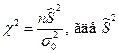 – исправленная выборочная дисперсия. Определяют
– исправленная выборочная дисперсия. Определяют 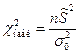 .
.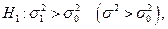 то для определения
то для определения 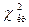 выбираем правостороннюю критическую область и по таблице распределения Пирсона (
выбираем правостороннюю критическую область и по таблице распределения Пирсона (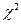 ) определяем
) определяем 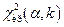 (на уровне значимости
(на уровне значимости 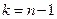 ). Если
). Если 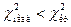 , то гипотезу
, то гипотезу 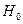 принимаем, если
принимаем, если 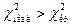 – отвергаем гипотезу
– отвергаем гипотезу 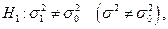 то строим двухстороннюю область, определяем левую
то строим двухстороннюю область, определяем левую 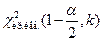 и правую
и правую 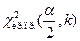 критические точки. Если
критические точки. Если 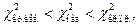 то гипотеза
то гипотеза 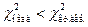 или
или 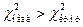 , то гипотеза
, то гипотеза 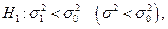 то строим левостороннюю критическую область, находим
то строим левостороннюю критическую область, находим 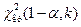 . Если
. Если 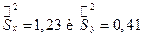 . При уровне значимости
. При уровне значимости 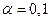 проверить гипотезу:
проверить гипотезу: 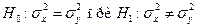 .
.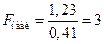 . Критическая область – двухсторонняя.
. Критическая область – двухсторонняя. 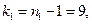
 ,
, 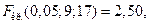 поскольку 3 > 2,5, то гипотеза отвергается (дисперсии различаются значимо).
поскольку 3 > 2,5, то гипотеза отвергается (дисперсии различаются значимо).


