
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел VIII. Теория вероятностейСодержание книги
Поиск на нашем сайте
Раздел VIII. Теория вероятностей Глава 21. Случайные события Понятие события В практической деятельности мы часто встречаемся с явлениями, исход которых нельзя предсказать заранее, т.к. он зависит от случая. При стрельбе из орудия по цели наблюдается рассеивание снарядов; уклонение точки попадания снаряда от цели – случайно даже при соблюдении некоторых условий. Необходимо научиться количественно оценивать случайные события, прогнозировать их течение. Решением возникающих при этом вопросов занимаются теория вероятностей и математическая статистика. Под случайным событием будем понимать все то, что может произойти, а может и не произойти при осуществлении некоторой совокупности условий. Например, первый родившийся в семье ребенок – мальчик, завтра в Белгороде выпадут осадки, и т.д. В дальнейшем вместо «совокупность условий осуществлена» будем говорить «произведено испытание», т.е. случайное событие – это результат испытания. Например, стрелок стреляет по мишени, разделенной на 10 областей. Выстрел – это испытание, попадание в определенную область – случайное событие. Случайные события обозначают заглавными буквами латинского алфавита A,B,C,D,…. Зафиксируем некоторое испытание, и будем рассматривать некоторую систему S событий A,B,C. Укажем некоторые соотношения, которые могут существовать между событиями системы S. 1. Если в результате испытания при каждом появлении события A наступает событие B, то говорят, что A является частным случаем B, и записывают этот факт в виде 2. Если 3. Произведением событий A и B называется такое событие AB, которое заключается в совместном наступлении этих событий. 4. Суммой событий A,B называется такое событие A + B, которое заключается в наступлении, по крайней мере, одного из этих событий. 5. Событие U называется достоверным, если оно c необходимостью должно произойти при каждом испытании. Все достоверные события равносильны. 6. Событие V называется невозможным, если оно не происходит ни при каком испытании. Все невозможные события равносильны. 7. Событие
8. События A и B называются несовместными, если их совместное наступление неосуществимо, т.е. 9. События Введенные операции над событиями удовлетворяют следующим правилам:
Одним из наглядных представлений случайных событий и операций над ними являются так называемые диаграммы Виена. Пусть внутри квадрата, изображенного на рисунке, наудачу выбирается точка, не лежащая ни на одной из нарисованных окружностей. Обозначим через А и В соответствующий выбор точки в левом и правом кругах. Области, заштрихованные на рисунке, изображают соответственно события
Элементы комбинаторики
Иногда необходимо из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа комбинаций. Такие задачи называются комбинаторными, раздел математики – комбинаторикой. Комбинаторика широко применяется в теории вероятности, теории управляющих систем и вычислительных машин и т.д. 1. Размещения. Пусть дано множество из n элементов. Размещениями называют комбинации, составленные из n элементов по m (0 Число размещений Пример. Из 30 учащихся надо выбрать комсорга, профорга, старосту. В группе все комсомольцы и члены профсоюза. Сколькими способами можно это сделать? A 2. Перестановки. Перестановкой из n элементов называется размещение из n элементов по n элементов. Отличаются друг от друга только порядком следования.
Пример. Сколькими способами можно расставить на 1 полке 6 книг? P 3.Сочетания Сочетаниями называют комбинации из n элементов по m элементов (0 Различаются неодинаковым составом элементов. Если отличаются лишь порядком следования элементов, то множества не считаются различными. Число сочетаний: Пример. В бригаде 25 человек. Необходимо выделить 4 человека для работы. Сколькими способами это можно сделать? Так как порядок выбранных рабочих не имеет значения, то C 4. Размещениями с повторениями называют упорядоченные последовательности, составленные из n элементов по m в каждом, где некоторые элементы (или все) могут быть одинаковы. Число размещений с повторениями равно: Пример. Сколькими способами можно распределить 6 пассажиров лифта по 3 этажам? На каждом из 3 этажей может выйти любое число пассажиров, поэтому число способов равно 5. Пусть размещения с повторениями содержат n элементов и при этом элемент а 1 повторяется n 1 раз, а
6. Если опыт состоит в выборе с возвращением m элементов множества, содержащего n элементов, но без упорядочивания, то различными исходами этого опыта будут всевозможные m –элементные наборы, отличающиеся составом. При этом отдельные наборы могут содержать повторяющиеся элементы. Получающиеся комбинации называется сочетаниями с повторениями. Их число Пример. В кондитерской имеются 8 видов пирожных. Сколько различных наборов по 3 пирожных можно составить? Порядок следования не учитывается, поэтому Кроме того, при решении комбинаторных задач используют следующие правила. Правило сумм. Если некоторый объект А может быть выбран из совокупности соответствующих объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно Правило произведений. Если объект А может быть выбран из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана Формула полной вероятности
Пусть событие А может произойти в результате появления одного и только одного события Н Теорема. Вероятность события А, которое может наступить при появлении одной из гипотез Н Доказательство. Событие А равносильно тому, что произойдет А и Н
Пример. На конвейер поступает продукция трех станков (50% – I, 30% – II, 20% – III). Брак составляет для первого станка 2%, для 2го – 3%, для 3го – 5%. Найти вероятность того, что случайно взятая деталь будет доброкачественной. Событие А – деталь доброкачественная. Возможны гипотезы: Н
По формуле полной вероятности: 21.9. Формула Байеса (Бейеса)
Пусть имеется полная группа несовместных гипотез Н По теореме умножения вероятностей:
Пример. Вероятность поражения цели при одном выстреле для первого орудия – 0,2, для второго – 0,1. Каждое орудие произвело по одному выстрелу, одно попало в цель. Какова вероятность, что удачный выстрел совершило первое орудие? Событие А – попадание в цель. Гипотеза Н
Формула Пуассона Если р = const, но близка к нулю (или Пример. Вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных. n = 1000, k = 5, l = n . p = 4. По таблице значений функции Пуассона: Распределения Биноминальное распределение Пусть производится n независимых испытаний, в каждом из которых вероятность появления события постоянна и равна р. В качестве дискретной случайной величины Х рассмотрим число появления события А в этих испытаниях. Х может принимать значения 0,1,2,3,4,…, n с вероятностями, определенными по формуле Бернулли: Полученная формула является аналитическим выражением биноминального закона распределения, т.е. биноминальным называется распределение вероятностей, определяемое формулой Бернулли. Запишем в виде таблицы:
Пример. Монета бросается два раза. Написать закон распределения дискретной случайной величины – числа появлений «герба». р = 0,5, q = 0,5,
Простейший поток событий
Рассмотрим события, которые наступают в случайные моменты времени. Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Например, поступление вызовов на АТС, прибытие самолетов в аэропорт, последовательность отказов элементов и т.д. Рассмотрим основные свойства потоков событий. Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета, при этом различные промежутки времени предполагаются непересекающимися. Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Таким образом, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем. Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности. Интенсивностью потока Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за 5 минут поступит: а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. По условию: а) б) в)
И его свойства Закон распределения полностью описывает случайную величину, однако иногда выгоднее пользоваться числами, которые описывают случайную величину суммарно – это числовые характеристики величин. Рассмотрим математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть дискретная случайная величина принимает значения Если дискретная случайная величина Х принимает счетное множество возможных значений, то Пример 1. Найти М (Х), если задан закон распределения:
Пример 2. Найти М (Х) числа появлений события А в одном испытании, если вероятность появления события А равна р. Пусть Х – число появлений события А, тогда Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Свойства дисперсии 1. Дисперсия постоянной величины равной нулю. D (C) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Если |C| > 1, то величина СХ имеет большие (по модулю) значения, поэтому D (CX)> D (X). 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D (X+Y) = D (X) + D (Y). Докажем:
Следствие: D (X+C) = D (X) + D (C) = D (X), С = const. 4. D (X – Y) = D (X) + D (Y). Докажем: D (X–Y) = D (X) + D (–Y) = D (X) + (–1)2 D (X) = = D (X) + D (Y). Теорема. Дисперсия числа появлений событий А в n независимых испытаниях, в каждом из которых вероятность появления события А p = const, равна npq = D (X),где Иначе. Дисперсия биноминального распределения равна D (X)= npq.
Случайной величины Непрерывную случайную величину можно задать функцией распределения, однако можно использовать и плотностью распределения. Плотностью распределения вероятностей непрерывной случайной величины Х называют производную от функции распределения: Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равно Доказательство: Если известна функция распределения, то Р (a £ X £ b) = F (b) – F (a). По формуле Ньютона-Лейбница: F (b) – F (a) = Пример. Дана плотность вероятности:
Найти вероятность того, что в результате испытания Х примет значение Î (0,5; 1). Р (0,5 < X < 1) = Функцию распределения можно найти по плотности распределения: F (x) = По известной функции распределения можно найти плотность: Пример. Найти F(x), если Если x £ a, f (x) = 0, то Свойства f (x) 1. f (x) ³ 0, т.к. F (x) – неубывающая функция, поэтому, 2. Вероятностный смысл
Нормальное распределение Нормальным распределением называется распределение вероятностей непрерывных случайных величин, которые описываются плотностью распределения
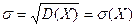 . .
График нормального распределения. Показательное распределение Показательным распределением называют распределение вероятностей случайных величин Х, которое описывается плотностью
Показательное распределение описывается одним параметром l, в этом его преимущество. Функция распределения:
Вероятность попадания в интервал (a,b) непрерывной случайной величины Х, распределенной по показательному закону: Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение:
Функция надежности Пусть элемент – это некоторое устройство. Пусть элемент начал работать в момент времени t о=0, а по истечении времени t происходит отказ. Обозначим через T непрерывную случайную величину – длительность безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время меньше t, то, следовательно, за время длительностью t наступит отказ. Функция распределения F (t) = P (T < t) определяет вероятность отказа за время t. Вероятность безотказной работы, т.е. противоположного события (T > t),равна: R (t) = P (T > t) = 1 – F (t). Функция надежности R (t) – функция, определяющая вероятность безотказной работы элемента за время t: R ( t ) = P ( T > t ). Пример. Время безотказной работы элемента распределено по показательному закону По условию,
Теорема Бернулли Пусть в каждом из n независимых испытаний вероятность p появления события А постоянна. Тогда как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Или Пусть Теорема Пуассона. Если в последовательности n независимых испытаний вероятность появления события А в каждом испытании равна Пусть случайная величина
И прямоугольник
Найдем вероятность того, что в результате испытания случайная точка попадет в полуполосу: Функция распределения Рассмотрим вероятность попадания в прямоугольник ABCD, заданий уравнениями сторон:
 
Вариационный ряд Рассмотрим пример. Токарь изготавливал в течение 10 дней следующее количество деталей: 5,6,5,7,7,7,8,5,6,5. Ранжируем эту выборку – разобьем на группы: 5,5,5,5 6,6 7,7,7 8 4 раза 2 раза 3 раза 1 раз. При ранжировании группы располагаются в порядке возрастания. Значение каждой группы называется вариантой. Число повторений в каждой группе называется частотой варианты. Полученную таблицу называют вариационным рядом.
В общем виде:
Графическое изображение вариационного ряда – полигон. Для непрерывного признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -й интервал. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны
Точечные оценки
Вариационный ряд характеризует случайную величину, но не в полной мере, поэтому используются характеристики, аналогичные теоретическим – М (х), D (х) и т.д. Эти числовые характеристики подсчитываются на основании выборки и называются точечными оценками (т.к. являются числами). Точечной оценкой характеристики Q называется некоторая функция Q* результатов наблюдений, значение которой принимают за приближение этой характеристики: 1. Несмещенность оценки: точечная оценка называется несмещенной, если ее математическое ожидание равно оценивающему параметру: 2. Состоятельность: точечная оценка называется состоятельной, если она при 3. Эффективность: точечная оценка считается эффективной, если она имеет (при заданном n) наименьшую дисперсию.
Основные точечные оценки
Выборочная средняя 2. Выборочная дисперсия: 3. Начальные и центральные моменты k - го порядка. Начальный момент k -го порядка:
Схема проверки гипотез 1. По условию задачи формулируют основную
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.251 (0.016 с.) |


 и
и  , то А=В. События A и B называются равносильными, если при каждом испытании они оба наступают либо не наступают.
, то А=В. События A и B называются равносильными, если при каждом испытании они оба наступают либо не наступают. называется противоположным событию А (и наоборот), если для них одновременно выполняются равенства
называется противоположным событию А (и наоборот), если для них одновременно выполняются равенства  . Иначе, два события называются противоположными, если одно из них обязательно должно произойти, причем наступление одного исключает возможность появления другого.
. Иначе, два события называются противоположными, если одно из них обязательно должно произойти, причем наступление одного исключает возможность появления другого. .
. образуют полную группу попарно несовместных событий, если события
образуют полную группу попарно несовместных событий, если события  несовместны и хотя бы одно из событий
несовместны и хотя бы одно из событий  (полная группа) и
(полная группа) и  (попарная несовместность). Иначе – события
(попарная несовместность). Иначе – события 
 . По диаграммам Виена легко проверяются правила сложения и умножения событий.
. По диаграммам Виена легко проверяются правила сложения и умножения событий.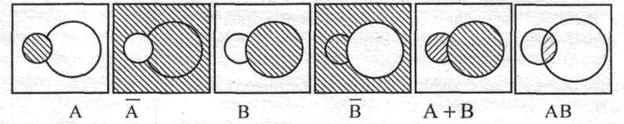
 m
m  или A
или A  =
=  . Полагаем, что 0! = 1.
. Полагаем, что 0! = 1. = 30 . 29 . 28 = 24360.
= 30 . 29 . 28 = 24360.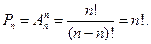
 = 6! = 720.
= 6! = 720. .
. =
=  .
. .
.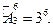
 повторяется n
повторяется n  раз,
раз,  . Такие упорядоченные последовательности называются перестановками с повторениями. Число их равно
. Такие упорядоченные последовательности называются перестановками с повторениями. Число их равно .
. .
.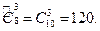
 способами.
способами. способами.
способами.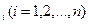 из некоторой полной группы несовместных событий (полная система). Н
из некоторой полной группы несовместных событий (полная система). Н 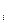
 обычно называют гипотезами.
обычно называют гипотезами. .
.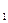 , либо А и Н
, либо А и Н 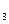 ,…, либо А и Н
,…, либо А и Н 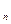 . Тогда по теоремам сложения (несовместных событий) и умножения
. Тогда по теоремам сложения (несовместных событий) и умножения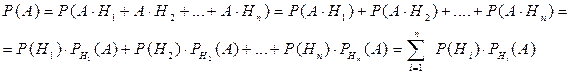
 – вероятность взять доброкачественное изделие, изготовленное 1м станком: P
– вероятность взять доброкачественное изделие, изготовленное 1м станком: P 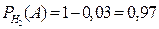 , P
, P 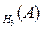 = 1–0,05 = 0,95. Вероятности гипотез даны по условию: P (H
= 1–0,05 = 0,95. Вероятности гипотез даны по условию: P (H  , P (H
, P (H 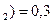 , P (H
, P (H 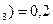 .
.

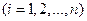 известны до опыта. Производится опыт, в результате которого зарегистрировано событие А. Известно, что этому событию наши гипотезы приписывали определенные вероятности P
известны до опыта. Производится опыт, в результате которого зарегистрировано событие А. Известно, что этому событию наши гипотезы приписывали определенные вероятности P 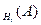
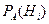 .
.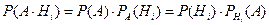 .
.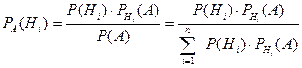 (i = 1,…, n). Это – формула Байеса, где
(i = 1,…, n). Это – формула Байеса, где 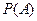 – вероятность появления события А.
– вероятность появления события А.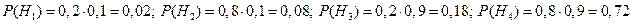 (
(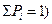 .
.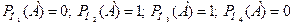 , т.е. гипотезы Н
, т.е. гипотезы Н 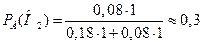 – вероятность того, что попало второе орудие;
– вероятность того, что попало второе орудие; 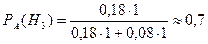 – вероятность того, что попало первое орудие.
– вероятность того, что попало первое орудие. ), а n достаточно велико, причем
), а n достаточно велико, причем  , то вероятность того, что в n испытаниях событие А наступит k раз:
, то вероятность того, что в n испытаниях событие А наступит k раз:  .
. , по таблице Лапласа вероятность равна 0,1763. Точное значение вероятности равно 0,1562.
, по таблице Лапласа вероятность равна 0,1763. Точное значение вероятности равно 0,1562.





 называют среднее число событий, которые появляются в единицу времени. Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона:
называют среднее число событий, которые появляются в единицу времени. Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона:  . Эта формула отражает все свойства простейшего потока, т.е. формулу Пуассона можно считать математической моделью простейшего потока событий.
. Эта формула отражает все свойства простейшего потока, т.е. формулу Пуассона можно считать математической моделью простейшего потока событий. По формуле Пуассона:
По формуле Пуассона:
 эти события практически невозможны.
эти события практически невозможны. – практически достоверное событие.
– практически достоверное событие. с вероятностями
с вероятностями  , тогда
, тогда  .
. , причем М (Х) существует, если ряд сходится абсолютно. М (Х) – неслучайная (постоянная) величина.
, причем М (Х) существует, если ряд сходится абсолютно. М (Х) – неслучайная (постоянная) величина.
 – событие А наступило с вероятностью р и
– событие А наступило с вероятностью р и  – событие А не наступило с вероятностью
– событие А не наступило с вероятностью 
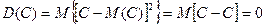 .
.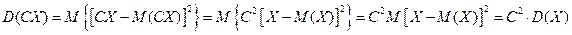 .
.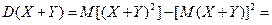
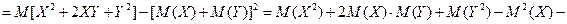

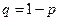 .
.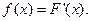
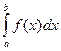 , т.е. Р (a < Х < b) =
, т.е. Р (a < Х < b) = 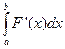 =
= 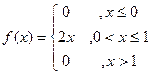 .
.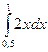 = 0,75.
= 0,75.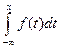 . Действительно, F (x) = P (X < x) или F (x) = P (–¥ < X < x), тогда
. Действительно, F (x) = P (X < x) или F (x) = P (–¥ < X < x), тогда  .
.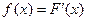 .
.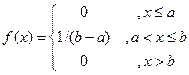 .
. , если
, если 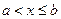 :
: 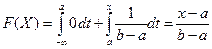 . Если
. Если 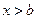 , то
, то 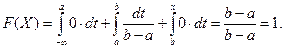
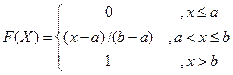 .
.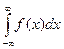 =1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение
=1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение  (–µ;µ) – достоверное событие, поэтому р = 1.
(–µ;µ) – достоверное событие, поэтому р = 1.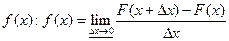 , тогда:
, тогда: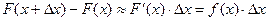 – вероятность того, что случайная величина примет значение
– вероятность того, что случайная величина примет значение 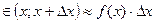 .
.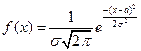 . Нормальное распределения определяются параметрами а и s. Покажем, что a=M (X),
. Нормальное распределения определяются параметрами а и s. Покажем, что a=M (X),  .
. . Введем:
. Введем:  , x = s Z+a, dx = s dZ,
, x = s Z+a, dx = s dZ,  Первое слагаемое равно нулю, т.к. функция нечетная, пределы интегрирования симметричны относительно начала координат,
Первое слагаемое равно нулю, т.к. функция нечетная, пределы интегрирования симметричны относительно начала координат,  (это – интеграл Пуассона). Таким образом, M(X) = a.
(это – интеграл Пуассона). Таким образом, M(X) = a. . Пусть
. Пусть  тогда
тогда 
 ,
, =1
=1

 , где l > 0 – const.
, где l > 0 – const.
 .
. (
( – по таблице).
– по таблице).
 .
.

 .
. , что позволяет определить, является ли закон распределения показательным.
, что позволяет определить, является ли закон распределения показательным. при
при  . Найти вероятность того, что элемент проработает безотказно 100 часов.
. Найти вероятность того, что элемент проработает безотказно 100 часов. Тогда
Тогда  – искомая вероятность безотказной работы.
– искомая вероятность безотказной работы. , где
, где 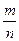 – частота появления события A.
– частота появления события A.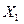 – число появлений события A в первом испытании,
– число появлений события A в первом испытании, 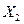 – во втором,
– во втором,  – в n -ом испытании,
– в n -ом испытании, 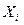 может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью
может принимать значения: 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью 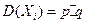 , так как
, так как 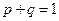 , то
, то 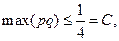
 , тогда по неравенству Чебышева:
, тогда по неравенству Чебышева: 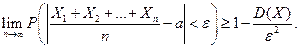
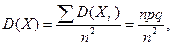
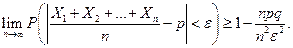 Каждая величина
Каждая величина 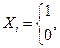 тогда
тогда 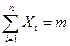 – числу появления события А в n испытаниях, тогда
– числу появления события А в n испытаниях, тогда 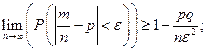 следовательно,
следовательно, 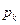 , то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей
, то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей 
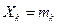 – число появлений события А в каждом испытании, тогда
– число появлений события А в каждом испытании, тогда 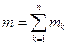 – число появлений события А в n испытаниях.
– число появлений события А в n испытаниях. 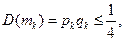
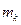 – независимые величины. Для случайной величины
– независимые величины. Для случайной величины 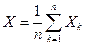 имеем:
имеем: 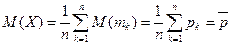 среднее арифметическое вероятностей;
среднее арифметическое вероятностей; 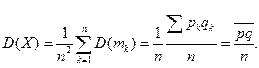 Тогда по неравенству Чебышева:
Тогда по неравенству Чебышева: 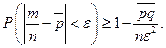 Переходя к пределу, получим доказываемое.
Переходя к пределу, получим доказываемое.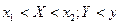 или в полуполосу
или в полуполосу 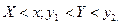
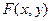 считается известной, она определяет вероятность попадания случайной точки в квадрант с вершиной
считается известной, она определяет вероятность попадания случайной точки в квадрант с вершиной 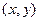 . Тогда вероятность попадания случайной точки в полуполосу равна:
. Тогда вероятность попадания случайной точки в полуполосу равна: 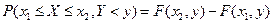 - это разность вероятностей попадания случайной точки в квадрант с вершиной
- это разность вероятностей попадания случайной точки в квадрант с вершиной 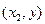 и вероятности попадания случайной точки в квадрант с вершиной
и вероятности попадания случайной точки в квадрант с вершиной 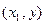 . Аналогично,
. Аналогично, 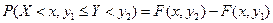 . Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
. Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.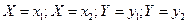 . Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD:
. Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD: 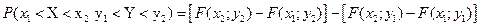 .
. Y
Y





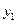


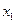
 X
X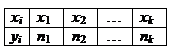
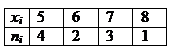
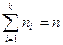 – объем выборки.
– объем выборки.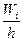 , где
, где 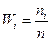 – относительная частота.
– относительная частота.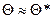 . Качество точечной оценки определяется характеристиками:
. Качество точечной оценки определяется характеристиками: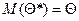 , т.е. совпадает с истинным значением.
, т.е. совпадает с истинным значением.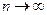 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.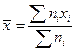 .
.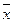 приближается к М (х), является несмещенной, состоятельной и эффективной.
приближается к М (х), является несмещенной, состоятельной и эффективной.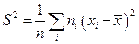 . S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию:
. S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию: 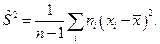
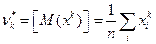 . Центральный момент k -го порядка:
. Центральный момент k -го порядка: 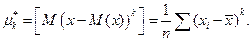
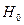 и
и 


