Как использовать метод доверительных интервалов для установления значимости коэффициента регрессии?
Похожие статьи вашей тематики
Если полученный коэффициент регрессии попадает в построенный доверительный интервал, то соответственно он считается значимым.
Как использовать метод доверительных интервалов для проверки гипотезы о
Конкретном значении коэффициента регрессии (отличном от нуля)?
Нужно проверить нулевую гипотезу (H0) о каком-то конкретном значении коэффициента 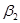 . Его возможных значений, близких к значению эксперимента, может быть несколько. Но, начиная с какого-то момента они будут отличаться настолько, что мы отклоним нулевую. Смысл доверительного интервала – найти условие (интервал), в котором наше гипотетическое . Его возможных значений, близких к значению эксперимента, может быть несколько. Но, начиная с какого-то момента они будут отличаться настолько, что мы отклоним нулевую. Смысл доверительного интервала – найти условие (интервал), в котором наше гипотетическое 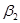 совместимо со значением коэффициента регрессии b совместимо со значением коэффициента регрессии b 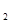 (т.е. значение (т.е. значение 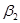 не опровергается оценкой b не опровергается оценкой b 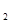 ). ).
Для построения интервала найдём табличные значения:
· выберем уровень значимости (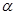 ) 1% или 5%. ) 1% или 5%.
· рассчитаем количество степеней свободы (n-2), вычисляем t  критическое при двустороннем интервале по таблице распределения Стьюдента. критическое при двустороннем интервале по таблице распределения Стьюдента.
После этого следует вычислить границы доверительного интервала следующим образом:

Как выбирается уровень доверительной вероятности при использовании метода
Доверительных интервалов при проверке значимости коэффициента регрессии?
Зависит от того, на каком уровне значимости (1% или 5%) отвергается нулевая гипотеза Н0. Если на 1% уровне, то строим 99% доверительный интервал, если на 5%, то 95% доверительный интервал. 99% интервал будет шире, чем 95%, так как t критич будет больше для 1% ого уровня значимости.
В чем сходство и различие методов проверки гипотез и доверительных интервалов?
Для двусторонних тестов они эквивалентны. Односторонних интервалов просто не бывает, а односторонние гипотезы вполне работают (ответ Черняка).
ТЕМА 7. Двусторонние и односторонние тесты.
В чем различие между двусторонним и односторонним критериями?
При двустороннем тесте мы проверяем гипотезу H0:β=β0(в частности, β=0), используя альтернативную гипотезу H1:β≠β0.
При одностороннем тесте альтернативная гипотеза меняется на H1:β>β0 и H1:β<β0 в зависимости от того, какое влияние оказывает x на y (положительное или отрицательное соответственно). При этом у нас должны быть веские причины считать, что это влияние положительно/отрицательно.
В каких случаях можно использовать односторонние критерии при проверке гипотез о коэффициенте регрессии, и что это дает?
Риск одностороннего критерия в том, что он может назвать значимой переменную, которая не является значимой на самом деле. Односторонний критерий – это шанс назвать вашу переменную значимой, когда двусторонний критерий не срабатывает.
Единственное условие, при котором вы можете его применять, это если гипотеза о значимости переменной и ее важности в уравнении регрессии была построена до того, как EViews разочаровал Вас. Это вопрос этики, поскольку тесты созданы для проверки гипотезы, придумывание гипотез по результатам теста – порочный круг.
Вы протестировали регрессию, получили что важный с вашей точки зрения коэффициент не значим на двустороннем уровне, но значим по одностороннему критерию. Тогда, логически и экономически обосновывая свою позицию, что «все равно, я считаю эту переменную важной», вы присуждаете ей значимость на одностороннем критерии.
Каково соотношение между двусторонним и односторонним тестами? Пусть двусторонний тест позволил отвергнуть нулевую гипотезу. Что можно сказать об одностороннем тесте?
Когда имеются основания для применения одностороннего теста, его следует предпочесть двустороннему. Односторонний критерий имеет меньшую вероятность ошибки второго рода, чем соответствующий двусторонний. Поэтому, когда нет необходимости применять двусторонний критерий, применяют односторонний.
Односторонний тест – тест на проверку гипотезы, в котором область принятия гипотезы имеет только одно критическое значение, в отличие от двустороннего теста, в котором область принятия гипотезы имеет два критических значения – меньшее и большее.
Если двусторонний тест отвергнул нулевую гипотезу, то есть вероятность принятия ее односторонним.
|