

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Построение доверительного интервала для оценки среднего значения генеральной совокупности
Чтобы найти границы доверительного интервала для среднего значения генеральной совокупности необходимо выполнить следующие действия:
1) по полученной выборке объема n вычислить среднее арифметическое 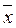 и стандартную ошибку среднего арифметического и стандартную ошибку среднего арифметического 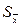 по формуле: по формуле:
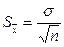 ; ;
2) задать доверительную вероятность 1 – α, исходя из цели исследования;
3) по таблице t -распределения Стьюдента (Приложение 4) найти граничное значение tα в зависимости от уровня значимости α и числа степеней свободы k = n – 1;
4) найти границы доверительного интервала по формуле:
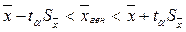 . .
Примечание: В практике научных исследований, когда закон распределения малой выборочной совокупности (n < 30) неизвестен или отличен от нормального, пользуются вышеприведенной формулой для приближенной оценки доверительных интервалов.
Доверительный интервал при n ≥ 30 находится по следующей формуле:
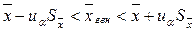 , ,
где u a – процентные точки нормированного нормального распределения, которые находятся по таблице 7.
Вопросы для самопроверки:
1. Сущность метода оценки эффективности методики тренировки.
2. Нормальный закон распределения. Сущность, значение.
3. Основные свойства кривой нормального распределения.
4. Правило трех сигм и его практическое применение.
5. Оценка нормальности распределения малой выборки.
6. Какие критерии и в каких случаях используются для сравнения средних попарно зависимых выборок?
7. Что характеризует доверительный интервал? Методика его определения.
ПРИЛОЖЕНИЯ
Приложение 1 – Критические точки распределения коэффициента корреляции. Односторонняя критическая область
| n
| α
| n
| α
| | 0,05
| 0,01
| 0,05
| 0,01
| |
| 0,988
| 0,9995
|
| 0,400
| 0,543
| |
| 0,900
| 0,980
|
| 0,389
| 0,529
| |
| 0,805
| 0,934
|
| 0,378
| 0,516
| |
| 0,729
| 0,882
|
| 0,369
| 0,503
| |
| 0,669
| 0,833
|
| 0,360
| 0,492
| |
| 0,621
| 0,789
|
| 0,323
| 0,445
| |
| 0,582
| 0,750
|
| 0,296
| 0,409
| |
| 0,549
| 0,715
|
| 0,275
| 0,381
| |
| 0,521
| 0,685
|
| 0,257
| 0,358
| |
| 0,497
| 0,658
|
| 0,243
| 0,338
| |
| 0,476
| 0,634
|
| 0,231
| 0,322
| |
| 0,457
| 0,612
|
| 0,211
| 0,295
| |
| 0,441
| 0,592
|
| 0,195
| 0,274
| |
| 0,426
| 0,574
|
| 0,183
| 0,257
| |
| 0,412
| 0,558
|
| 0,173
| 0,242
| |
|
|
|
| 0,164
| 0,230
|
Двусторонняя критическая область
| n
| α
| N
| Α
| | 0,05
| 0,01
| 0,05
| 0,01
| |
| 0,950
| 0,990
|
| 0,388
| 0,496
| |
| 0,878
| 0,959
|
| 0,381
| 0,487
| |
| 0,811
| 0,917
|
| 0,374
| 0,476
| |
| 0,754
| 0,874
|
| 0,367
| 0,470
| |
| 0,707
| 0,834
|
| 0,361
| 0,463
| |
| 0,666
| 0,798
|
| 0,322
| 0,435
| |
| 0,632
| 0,766
|
| 0,310
| 0,407
| |
| 0,602
| 0,736
|
| 0,292
| 0,384
| |
| 0,576
| 0,708
|
| 0,277
| 0,364
| |
| 0,553
| 0,684
|
| 0,253
| 0,333
| |
| 0,532
| 0,661
|
| 0,234
| 0,308
| |
| 0,514
| 0,644
|
| 0,219
| 0,288
| |
| 0,497
| 0,623
|
| 0,206
| 0,272
| |
| 0,482
| 0,606
|
| 0,196
| 0,258
| |
| 0,468
| 0,590
|
| 0,175
| 0,230
| | n
| Α
| n
| Α
| | 0,05
| 0,01
| 0,05
| 0,01
| |
| 0,456
| 0,575
|
| 0,160
| 0,210
| |
| 0,444
| 0,561
|
| 0,138
| 0,182
| |
| 0,433
| 0,549
|
| 0,124
| 0,163
| |
| 0,423
| 0,537
|
| 0,113
| 0,148
| |
| 0,413
| 0,526
|
| 0,098
| 0,128
| |
| 0,404
| 0,515
|
| 0,088
| 0,115
| |
| 0,396
| 0,505
|
| 0,062
| 0,081
|
Приложение 2 – Значения коэффициентов ank, используемых для расчета критерия W проверки нормальности распределения
| k
| n
| |
|
|
|
|
|
|
|
| |
| 0,7071
| 0,6872
| 0,6646
| 0,6431
| 0,6233
| 0,6052
| 0,5888
| 0,5739
| |
|
| 0,1677
| 0,2413
| 0,2806
| 0,3031
| 0,3164
| 0,3244
| 0,3291
| |
|
|
|
| 0,0875
| 0,1401
| 0,1743
| 0,1976
| 0,2141
| |
|
|
|
|
|
| 0,0561
| 0,0947
| 0,1224
| |
|
|
|
|
|
|
|
| 0,0399
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,5601
| 0,5475
| 0,5359
| 0,5251
| 0,5150
| 0,5056
| 0,4968
| 0,4886
| |
| 0,3315
| 0,3325
| 0,3325
| 0,3318
| 0,3306
| 0,3290
| 0,3273
| 0,3253
| |
| 0,2260
| 0,2347
| 0,2412
| 0,2460
| 0,2495
| 0,2521
| 0,2540
| 0,2553
| |
| 0,1429
| 0,1585
| 0,1707
| 0,1802
| 0,1878
| 0,1939
| 0,1988
| 0,2027
| |
| 0,0695
| 0,0922
| 0,1099
| 0,1240
| 0,1353
| 0,1447
| 0,1524
| 0,1587
| |
|
| 0,0303
| 0,0539
| 0,0727
| 0,0880
| 0,1005
| 0,1109
| 0,1197
| |
|
|
|
| 0,0240
| 0,0433
| 0,0593
| 0,0725
| 0,0837
| |
|
|
|
|
|
| 0,0196
| 0,0359
| 0,0496
| |
|
|
|
|
|
|
|
| 0,0163
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,4808
| 0,4734
| 0,4643
| 0,4590
| 0,4542
| 0,4493
| 0,4450
| 0,4407
| |
| 0,3232
| 0,3211
| 0,3185
| 0,3156
| 0,3126
| 0,3098
| 0,3069
| 0,3043
| |
| 0,2561
| 0,2565
| 0,2578
| 0,2571
| 0,2563
| 0,2554
| 0,2543
| 0,2533
| |
| 0,2059
| 0,2085
| 0,2119
| 0,2131
| 0,2139
| 0,2145
| 0,2148
| 0,2151
| |
| 0,1641
| 0,1686
| 0,1736
| 0,1764
| 0,1787
| 0,1807
| 0,1822
| 0,1836
| |
| 0,1271
| 0,1334
| 0,1399
| 0,1443
| 0,1480
| 0,1512
| 0,1539
| 0,1563
| |
| 0,0932
| 0,1013
| 0,1092
| 0,1150
| 0,1201
| 0,1245
| 0,1283
| 0,1316
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,0612
| 0,0711
| 0,0804
| 0,0878
| 0,0941
| 0,0997
| 0,1046
| 0,1089
| |
| 0,0303
| 0,0422
| 0,0530
| 0,0616
| 0,0696
| 0,0764
| 0,0823
| 0,0876
| |
|
| 0,0140
| 0,0263
| 0,0368
| 0,0549
| 0,0539
| 0,0610
| 0,0672
| |
|
|
|
| 0,0122
| 0,0228
| 0,0321
| 0,0403
| 0,0476
| |
|
|
|
|
|
| 0,0107
| 0,0200
| 0,0284
| |
|
|
|
|
|
|
|
| 0,0094
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,4366
| 0,4328
| 0,4291
| 0,4254
| 0,4220
| 0,4188
| 0,4156
| 0,4127
| |
| 0,3018
| 0,2992
| 0,2988
| 0,2944
| 0,2921
| 0,2898
| 0,2876
| 0,2854
| |
| 0,2522
| 0,2510
| 0,2499
| 0,2487
| 0,2475
| 0,2463
| 0,2451
| 0,2439
| |
| 0,2152
| 0,2151
| 0,2150
| 0,2148
| 0,2145
| 0,2141
| 0,2137
| 0,2132
| |
| 0,1848
| 0,1867
| 0,1864
| 0,1870
| 0,1874
| 0,1878
| 0,1880
| 0,1882
| |
| 0,1584
| 0,1601
| 0,1616
| 0,1630
| 0,1641
| 0,1651
| 0,1660
| 0,1667
| |
| 0,1346
| 0,1372
| 0,1396
| 0,1415
| 0,1433
| 0,1449
| 0,1463
| 0,1475
| |
| 0,1128
| 0,1162
| 0,1192
| 0,1219
| 0,1243
| 0,1265
| 0,1284
| 0,1301
| |
| 0,0923
| 0,0955
| 0,1002
| 0,1036
| 0,1066
| 0,1093
| 0,1118
| 0,1140
| |
| 0,0728
| 0,0778
| 0,0822
| 0,0862
| 0,0899
| 0,0931
| 0,0961
| 0,0988
| |
| 0,0540
| 0,0598
| 0,0650
| 0,0697
| 0,0739
| 0,0777
| 0,0812
| 0,0844
| |
| 0,0358
| 0,0424
| 0,0483
| 0,0537
| 0,0585
| 0,0629
| 0,0669
| 0,0706
| |
| 0,0178
| 0,0253
| 0,0320
| 0,0381
| 0,0435
| 0,0485
| 0,0530
| 0,0572
| |
|
| 0,0084
| 0,0159
| 0,0227
| 0,0289
| 0,0344
| 0,0395
| 0,0441
| |
|
|
|
| 0,0076
| 0,0144
| 0,0206
| 0,0262
| 0,0314
| |
|
|
|
|
|
| 0,0068
| 0,0131
| 0,0187
| |
|
|
|
|
|
|
|
| 0,0062
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,4096
| 0,4068
| 0,4040
| 0,4015
| 0,3989
| 0,3964
| 0,3940
| 0,3917
| |
| 0,2834
| 0,2813
| 0,2794
| 0,2774
| 0,2755
| 0,2737
| 0,2719
| 0,2701
| |
| 0,2427
| 0,2415
| 0,2403
| 0,2391
| 0,2380
| 0,2368
| 0,2357
| 0,2345
| |
| 0,2127
| 0,2121
| 0,2116
| 0,2110
| 0,2104
| 0,2098
| 0,2091
| 0,2085
| |
| 0,1883
| 0,1883
| 0,1883
| 0,1881
| 0,1880
| 0,1878
| 0,1876
| 0,1874
| |
| 0,1673
| 0,1678
| 0,1683
| 0,1686
| 0,1689
| 0,1691
| 0,1693
| 0,1694
| |
| 0,1487
| 0,1496
| 0,1505
| 0,1513
| 0,1520
| 0,1526
| 0,1531
| 0,1535
| |
| 0,1317
| 0,1331
| 0,1344
| 0,1356
| 0,1366
| 0,1376
| 0,1384
| 0,1392
| |
| 0,1160
| 0,1179
| 0,1196
| 0,1211
| 0,1225
| 0,1237
| 0,1249
| 0,1259
| |
| 0,1013
| 0,1036
| 0,1056
| 0,1075
| 0,1092
| 0,1108
| 0,1123
| 0,1136
| |
| 0,0873
| 0,9000
| 0,0924
| 0,0947
| 0,0967
| 0,0986
| 0,1004
| 0,1020
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,0739
| 0,0770
| 0,0798
| 0,0824
| 0,0848
| 0,0870
| 0,0891
| 0,0909
| |
| 0,0610
| 0,0645
| 0,0677
| 0,0706
| 0,0733
| 0,0759
| 0,0782
| 0,0804
| |
| 0,0484
| 0,0523
| 0,0559
| 0,0592
| 0,0622
| 0,0651
| 0,0677
| 0,0701
| |
| 0,0361
| 0,0404
| 0,0444
| 0,0481
| 0,0515
| 0,0546
| 0,0575
| 0,0602
| |
| 0,0239
| 0,0287
| 0,0331
| 0,0372
| 0,0409
| 0,0444
| 0,0476
| 0,0506
| |
| 0,0119
| 0,0172
| 0,0220
| 0,0264
| 0,0305
| 0,0343
| 0,0379
| 0,0411
| |
|
| 0,0057
| 0,0110
| 0,0156
| 0,0202
| 0,0244
| 0,0283
| 0,0318
| |
|
|
|
| 0,0053
| 0,0101
| 0,0146
| 0,0188
| 0,0227
| |
|
|
|
|
|
| 0,0049
| 0,0094
| 0,0136
| |
|
|
|
|
|
|
|
| 0,0045
| | k
| n
| |
|
|
|
|
|
|
|
| |
| 0,3894
| 0,3872
| 0,3850
| 0,3830
| 0,3808
| 0,3789
| 0,3770
| 0,3751
| |
| 0,2684
| 0,2667
| 0,2651
| 0,2635
| 0,2620
| 0,2604
| 0,2589
| 0,2574
| |
| 0,2334
| 0,2323
| 0,2312
| 0,2302
| 0,2291
| 0,2281
| 0,2271
| 0,2260
| |
| 0,2078
| 0,2072
| 0,2065
| 0,2058
| 0,2052
| 0,2045
| 0,2038
| 0,2032
| |
| 0,1871
| 0,1868
| 0,1865
| 0,1862
| 0,1859
| 0,1855
| 0,1851
| 0,1847
| |
| 0,1695
| 0,1695
| 0,1695
| 0,1695
| 0,1695
| 0,1693
| 0,1692
| 0,1691
| |
| 0,1539
| 0,1542
| 0,1545
| 0,1548
| 0,1550
| 0,1551
| 0,1553
| 0,1554
| |
| 0,1398
| 0,1405
| 0,1410
| 0,1416
| 0,1420
| 0,1423
| 0,1427
| 0,1430
| |
| 0,1269
| 0,1278
| 0,1286
| 0,1293
| 0,1300
| 0,1306
| 0,1312
| 0,1317
| |
| 0,1149
| 0,1160
| 0,1170
| 0,1180
| 0,1189
| 0,1197
| 0,1205
| 0,1212
| |
| 0,1035
| 0,1049
| 0,1062
| 0,1073
| 0,1085
| 0,1095
| 0,1105
| 0,1113
| |
| 0,0927
| 0,0943
| 0,0959
| 0,0972
| 0,0986
| 0,0998
| 0,1010
| 0,1020
| |
| 0,0824
| 0,0842
| 0,0860
| 0,0876
| 0,0882
| 0,0906
| 0,0919
| 0,0932
| |
| 0,0724
| 0,0745
| 0,0765
| 0,0783
| 0,0801
| 0,0817
| 0,0832
| 0,0846
| |
| 0,0628
| 0,0651
| 0,0673
| 0,0694
| 0,0713
| 0,0731
| 0,0748
| 0,0764
| |
| 0,0534
| 0,0560
| 0,0584
| 0,0607
| 0,0628
| 0,0648
| 0,0667
| 0,0685
| |
| 0,0442
| 0,0471
| 0,0497
| 0,0522
| 0,0546
| 0,0568
| 0,0588
| 0,0608
| |
| 0,0352
| 0,0383
| 0,0412
| 0,0439
| 0,0465
| 0,0489
| 0,0511
| 0,0532
| |
| 0,0263
| 0,0296
| 0,0328
| 0,0357
| 0,0385
| 0,0411
| 0,0436
| 0,0459
| |
| 0,0175
| 0,0211
| 0,0245
| 0,0277
| 0,0307
| 0,0335
| 0,0361
| 0,0386
| |
| 0,0087
| 0,0126
| 0,0163
| 0,0197
| 0,0229
| 0,0259
| 0,0288
| 0,0314
| |
|
| 0,0042
| 0,0081
| 0,0118
| 0,0153
| 0,0185
| 0,0215
| 0,0244
| |
|
|
|
| 0,0039
| 0,0076
| 0,0111
| 0,0143
| 0,0174
| |
|
|
|
|
|
| 0,0037
| 0,0071
| 0,0104
| |
|
|
|
|
|
|
|
| 0,0035
|
Приложение 3 – Критические точки распределения критерия W Шапиро и Уилка, используемого для проверки гипотезы о нормальном распределении генеральной совокупности
| n
| α
| n
| α
| n
| α
| | 0,05
| 0,01
| 0,05
| 0,01
| 0,05
| 0,01
| |
| 0,767
| 0,753
|
| 0,901
| 0,863
|
| 0,934
| 0,910
| |
| 0,748
| 0,687
|
| 0,905
| 0,868
|
| 0,935
| 0,912
| |
| 0,762
| 0,686
|
| 0,908
| 0,873
|
| 0,936
| 0,914
| |
| 0,786
| 0,713
|
| 0,911
| 0,878
|
| 0,938
| 0,916
| |
| 0,803
| 0,730
|
| 0,914
| 0,881
|
| 0,939
| 0,917
| |
| 0,818
| 0,749
|
| 0,916
| 0,884
|
| 0,940
| 0,919
| |
| 0,829
| 0,764
|
| 0,918
| 0,888
|
| 0,941
| 0,920
| |
| 0,842
| 0,791
|
| 0,920
| 0,891
|
| 0,942
| 0,922
| |
| 0,850
| 0,792
|
| 0,923
| 0,894
|
| 0,943
| 0,923
| |
| 0,859
| 0,805
|
| 0,924
| 0,896
|
| 0,944
| 0,924
| |
| 0,866
| 0,814
|
| 0,926
| 0,898
|
| 0,945
| 0,926
| |
| 0,874
| 0,825
|
| 0,927
| 0,900
|
| 0,945
| 0,927
| |
| 0,881
| 0,835
|
| 0,929
| 0,902
|
| 0,946
| 0,928
| |
| 0,887
| 0,844
|
| 0,930
| 0,904
|
| 0,947
| 0,929
| |
| 0,892
| 0,851
|
| 0,931
| 0,906
|
| 0,947
| 0,929
| |
| 0,897
| 0,858
|
| 0,933
| 0,908
|
| 0,947
| 0,950
|
Приложение 4 – Критические точки распределения критерия t Стьюдента
| Число степеней свободы k
| Уровень значимости α
(двусторонняя критическая область)
| | 0,10
| 0,05
| 0,02
| 0,01
| 0,002
| 0,001
| |
| 6,31
| 12,71
| 31,82
| 63,66
| 318,31
| 636,62
| |
| 2,92
| 4,30
| 6,96
| 9,92
| 22,33
| 31,60
| |
| 2,35
| 3,18
| 4,54
| 5,84
| 10,21
| 12,92
| |
| 2,13
| 2,78
| 3,75
| 4,60
| 7,17
| 8,61
| |
| 2,02
| 2,57
| 3,36
| 4,03
| 5,89
| 6,87
| |
| 1,94
| 2,45
| 3,14
| 3,71
| 5,21
| 5,96
| |
| 1,89
| 2,36
| 3,00
| 3,50
| 4,79
| 5,41
| |
| 1,86
| 2,31
| 2,90
| 3,36
| 4,50
| 5,04
| |
| 1,83
| 2,26
| 2,82
| 3,25
| 4,30
| 4,78
| |
| 1,81
| 2,23
| 2,76
| 3,17
| 4,14
| 4,59
| |
| 1,80
| 2,20
| 2,72
| 3,11
| 4,02
| 4,44
| |
| 1,78
| 2,18
| 2,68
| 3,05
| 3,93
| 4,32
| |
| 1,77
| 2,16
| 2,65
| 3,01
| 3,85
| 4,22
| |
| 1,76
| 2,14
| 2,62
| 2,98
| 3,79
| 4,14
| |
| 1,75
| 2,13
| 2,60
| 2,95
| 3,73
| 4,07
| | Число степеней свободы k
| Уровень значимости α
(двусторонняя критическая область)
| | 0,10
| 0,05
| 0,02
| 0,01
| 0,002
| 0,001
| |
| 1,75
| 2,12
| 2,58
| 2,92
| 3,69
| 4,01
| |
| 1,74
| 2,11
| 2,57
| 2,90
| 3,65
| 3,97
| |
| 1,73
| 2,10
| 2,55
| 2,88
| 3,61
| 3,92
| |
| 1,73
| 2,09
| 2,54
| 2,86
| 3,58
| 3,88
| |
| 1,72
| 2,09
| 2,53
| 2,85
| 3,55
| 3,85
| |
| 1,72
| 2,08
| 2,52
| 2,83
| 3,53
| 3,82
| |
| 1,72
| 2,07
| 2,51
| 2,82
| 3,50
| 3,79
| |
| 1,71
| 2,07
| 2,50
| 2,81
| 3,48
| 3,77
| |
| 1,71
| 2,06
| 2,49
| 2,80
| 3,47
| 3,75
| |
| 1,71
| 2,06
| 2,49
| 2,79
| 3,45
| 3,73
| |
| 1,71
| 2,06
| 2,48
| 2,78
| 3,43
| 3,71
| |
| 1,70
| 2,05
| 2,47
| 2,77
| 3,42
| 3,69
| |
| 1,70
| 2,05
| 2,47
| 2,76
| 3,41
| 3,67
| |
| 1,70
| 2,05
| 2,46
| 2,76
| 3,40
| 3,66
| |
| 1,70
| 2,04
| 2,46
| 2,75
| 3,39
| 3,65
| |
| 1,68
| 2,02
| 2,42
| 2,70
| 3,31
| 3,55
| |
| 1,67
| 2,00
| 2,39
| 2,66
| 3,23
| 3,46
| |
| 1,66
| 1,98
| 2,36
| 2,62
| 3,16
| 3,37
| | ∞
| 1,64
| 1,96
| 2,33
| 2,58
| 3,09
| 3,29
| | 0,05
| 0,025
| 0,01
| 0,005
| 0,001
| 0,0005
| | Уровень значимости α
(односторонняя критическая область)
|
Приложение 5 – Критические точки распределения критерия Уилкоксона, используемого для сравнения двух попарно зависимых выборок
| n
| α
| n
| α
| n
| α
| | 0,05
| 0,01
| 0,05
| 0,01
| 0,05
| 0,01
| |
|
| –
|
|
|
|
|
|
| |
|
| –
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Приложение 6 – Некоторые статистические функции табличного процессора Microsoft Excel
| Функция
| Описание
| | ДИСП
| Оценивает дисперсию по выборке (логические значения и текст игнорируются).
| | ДОВЕРИТ
| Возвращает доверительный интервал для среднего генеральной совокупности.
| | КВАДРОТКЛ
| Возвращает сумму квадратов отклонений точек данного от среднего по выборке.
| | КОРРЕЛ
| Возвращает коэффициент корреляции между двумя множествами данных.
| | МАКС
| Возвращает максимальное значение из списка аргументов. Логические значения или текст игнорируются.
| | МЕДИАНА
| Возвращает медиану исходных чисел.
| | МИН
| Возвращает минимальное значение из списка аргументов. Логические значения или текст игнорируются.
| | МОДА
| Возвращает значение моды множества данных.
| | ПИРСОН
| Возвращает коэффициент корреляции Пирсона, r.
| | СРЗНАЧ
| Возвращает среднее (арифметическое) своих аргументов, которые могут быть числами или именами, массивами или ссылками на ячейки с числами.
| | СТАНДОТКЛОН
| Оценивает стандартное отклонение по выборке. Логические значения или текст игнорируются.
| | СТЬЮДРАСПОБР
| Возвращает обратное распределение Стьюдента.
| | СЧЁТ
| Подсчитывает количество чисел в списке аргументов.
|
Литература
1. Годик, М.А. Спортивная метрология: учеб. для ин-тов физ. культуры / М.А. Годик. М., 1988.
2. Основы математической статистики: уч. пособие для ин-тов физ. культуры / под общ. ред. В.С. Иванова. М., 1990.
3. Спортивная метрология: учеб. для ин-тов физ. культуры / под общ. ред. В.М. Зациорского. М., 1982.
4. Основы педагогических измерений. Вопросы разработки и использования педагогических тестов: учеб.-метод. пособие / под общ. ред. В.Д. Скаковского. Минск, 2009.
5. Гинзбург, Г.И. Расчетно-графические работы по спортивной метрологии / Г.И. Гинзбург, В.Г. Киселев. Минск, 1984.
|



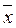 и стандартную ошибку среднего арифметического
и стандартную ошибку среднего арифметического 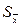 по формуле:
по формуле: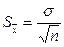 ;
;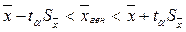 .
.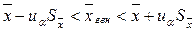 ,
,


