Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная и статистическая взаимосвязиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В спортивных исследованиях между изучаемыми показателями часто обнаруживается взаимосвязь. Вид ее бывает различным. Например, определение ускорения по известным данным скорости, второй закон Ньютона и другие характеризуют так называемую функциональную зависимость, или взаимосвязь, при которой каждому значению одного показателя соответствует строго определенное значение другого. К другому виду взаимосвязи относят, например, зависимость веса от длины тела. Одному значению длины тела может соответствовать несколько значений веса и наоборот. В таких случаях, когда одному значению одного показателя соответствует несколько значений другого, взаимосвязь называют статистической. Изучению статистической взаимосвязи между различными показателями в спортивных исследованиях уделяют большое внимание, поскольку это позволяет вскрыть некоторые закономерности и в дальнейшем описать их как словесно, так и математически с целью использования в практической работе тренера и педагога. Среди статистических взаимосвязей наиболее важны корреляционные. Корреляция – это статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания (среднего значения) другой. Например, толкание ядра 3 кг и 5 кг. Улучшение результатов толкания ядра 3 кг вызывает улучшение (в среднем) результата в толкании ядра весом 5 кг. Статистический метод, который используется для исследования взаимосвязей, называется корреляционным анализом. Основной задачей его является определение формы, тесноты и направленности взаимосвязи изучаемых показателей. Корреляционный анализ позволяет исследовать только статистическую взаимосвязь. Он широко используется в теории тестов для оценки их надежности и информативности. Различные шкалы измерений, как будет показано дальше, требуют разных вариантов корреляционного анализа.
Корреляционное поле Анализ взаимосвязи начинается с графического представления результатов измерений в прямоугольной системе координат. Предположим, что у шести испытуемых зарегистрирован такой показатель, как число подтягиваний на перекладине, до начала подготовительного периода тренировки (X) и после его окончания (Y). Запишем результаты измерений:
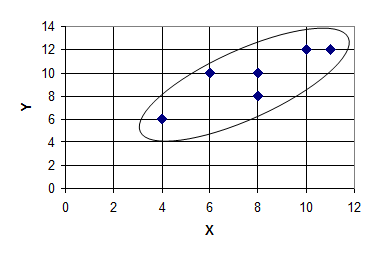
Для этих результатов построим график, на оси абсцисс которого отложим результаты X, а на оси ординат – результаты Y. Таким образом, каждая пара результатов в прямоугольной системе координат будет отображаться точкой (рис. 6).
Рисунок 6 – Корреляционное поле (линейная зависимость)
Такая графическая зависимость называется диаграммой рассеивания или корреляционным полем. Визуальный анализ графика позволяет выявить форму зависимости (по крайней мере, сделать предположение). В данном случае эта форма близка к обычной геометрической фигуре – эллипсу. Такую форму мы будем называть линейной зависимостью или линейной формой взаимосвязи. Однако на практике можно встретить и иную форму взаимосвязи (например, рис. 7). Эта зависимость, экспериментально полученная при подачах в теннисе, является характерной для нелинейной формы взаимосвязи, или нелинейной зависимости.
Рисунок 7 – Корреляционное поле (нелинейная зависимость): по абсциссе – скорость ракетки, по ординате – скорость вылета мяча
Таким образом, визуальный анализ корреляционного поля позволяет выявить форму статистической зависимости – линейную или нелинейную. Иными словами, если статистическая связь между явлениями выражается уравнением прямой линии
Оценка тесноты взаимосвязи Для оценки тесноты линейной взаимосвязи в корреляционном анализе используется значение (абсолютная величина) специального показателя – коэффициента корреляции. Абсолютное значение (модуль числа) любого коэффициента корреляции лежит в пределах от 0 до 1. Объясняют (интерпретируют) абсолютное значение коэффициента корреляции следующим образом: – коэффициент корреляции равен 1,00 (функциональная взаимосвязь, т.е. значению одного показателя соответствует только одно значение другого показателя); – коэффициент корреляции равен 0,99 – 0,70 (сильная статистическая взаимосвязь); – коэффициент корреляции равен 0,69 – 0,50 (средняя статистическая взаимосвязь); – коэффициент корреляции равен 0,49 – 0,20 (слабая статистическая взаимосвязь); – коэффициент корреляции равен 0,19 – 0,01 (очень слабая статистическая взаимосвязь); – коэффициент корреляции равен 0,00 (корреляция не обнаружена). На рисунках 8 и 9 приведены примеры двух различных зависимостей.
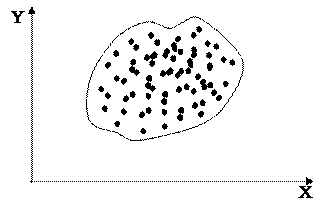
Рисунок 8 – Зависимость между становой силой и результатами в толкании ядра (n = 80). Пример очень слабой корреляционной зависимости. Коэффициент корреляции равен 0,09. По абсциссе – становая сила, по ординате – результат толкания ядра
Таким образом, значение (абсолютная величина) коэффициента корреляции, изменяясь в пределах от 0 до 1, позволяет оценивать тесноту взаимосвязи. Кроме тесноты нас будет интересовать и направленность взаимосвязи.
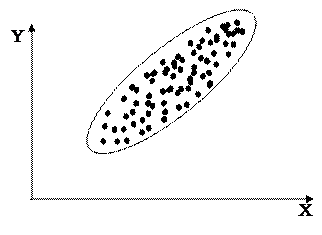
Рисунок 9 – Зависимость между результатами в толкании ядра разного веса (n = 80). Пример сильной корреляционной зависимости. Коэффициент корреляции равен 0,892. По абсциссе – результат толкания ядра 5 кг, по ординате – результат толкания ядра 3 кг
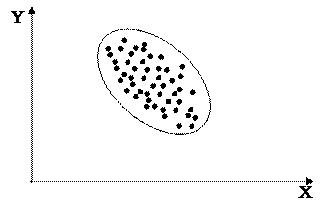
Рисунок 10 – Зависимость между результатами в беге на 100 м и прыжками в длину с разбега (n = 50). Пример отрицательной взаимосвязи: коэффициент корреляции равен –0,628. С уменьшением времени бега (при увеличении скорости) растут результаты в прыжках. По абсциссе – результаты в беге на 100 м, по ординате – в прыжках в длину
Направленность взаимосвязи Диаграмма рассеяния на рисунке 9, кроме сильной статистической взаимосвязи, имеет еще одну особенность – прямо пропорциональную тенденцию зависимости. Это значит, что улучшение, например, результата в толкании ядра весом 3 кг вызывает улучшение (в среднем) результата в толкании ядра весом 5 кг. На рисунке 10 представлена диаграмма обратно пропорциональной зависимости. В этом случае увеличение одного показателя связано с уменьшением другого (в среднем). Направленность зависимости отражается в знаке коэффициента корреляции. Знак «+» указывает на прямую пропорциональную или положительную взаимосвязь; знак «–» говорит об обратной или отрицательной взаимосвязи (рис. 11).

Рисунок 11 – Примеры взаимосвязей: а) нелинейная форма зависимости; б) отсутствие статистической зависимости (коэффициент корреляции = 0); в) функциональная зависимость(коэффициент корреляции = +1); г) положительная зависимость (коэффициент корреляции > 0); д) отрицательная зависимость (коэффициент корреляции < 0)
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.215 (0.009 с.) |

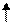


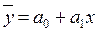 , то её называют линейной связью, если уравнением кривой (
, то её называют линейной связью, если уравнением кривой (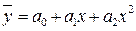 - парабола;
- парабола; 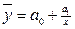 - гипербола и т.д.), то такую связь называют нелинейной. Это имеет существенное значение для следующего шага в анализе – выбора и вычисления соответствующего коэффициента корреляции.
- гипербола и т.д.), то такую связь называют нелинейной. Это имеет существенное значение для следующего шага в анализе – выбора и вычисления соответствующего коэффициента корреляции.