
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление рядов распределения и их графические представленияСодержание книги
Поиск на нашем сайте В процессе наблюдения или измерения какого-либо показателя получают ряд чисел. Численные результаты подразделяют на дискретные и непрерывные. К дискретным относят число подтягиваний на перекладине, число попыток и т.д., то есть результаты, выражаемые целым числом; к непрерывным – время прохождения дистанции, время реакции, скорость движения и т.п., то есть результаты, которые могут выражаться дробным числом, в частности, бесконечной дробью. Генеральной совокупностью называется совокупность всех объектов, характеристики которых требуется определить. Выборочной совокупностью, или просто выборкой, называется часть объектов, определённым образом выбранных из общей генеральной совокупности. Способы отбора: - случайный; - по определённой схеме; - смешанный (сочетание первого и второго способов). Например, длина тела студентов какого-либо учреждения высшего образования Республики Беларусь – выборочная совокупность, а длина тела студентов всех учреждений высшего образования – генеральная; в то же время длина тела студентов Беларуси – выборка по отношению к генеральной совокупности – всем студентам земного шара. Генеральную совокупность мысленно можно представить так: это все объекты наблюдения (например, спортсмены), которые обладают теми же свойствами, что и объекты выборки. В самом общем случае под генеральной совокупностью понимают совокупность всех мыслимых значений наблюдений, которые могли бы быть сделанными при данном комплексе условий. Один из центральных вопросов статистики: как обобщить результаты, полученные на выборке, на всей генеральной совокупности? Предположим, что исследователь проводил эксперименты на группе тяжелоатлетов III разряда и нашел, что один из методов тренировки лучше, чем другие. Можно ли распространить его данные на всех тяжелоатлетов III разряда, или же сделанные им выводы справедливы только для той группы спортсменов, в которой проводился эксперимент? Если исследованием охвачена вся генеральная совокупность, оно называется сплошным. Например, если кому-либо удалось обследовать всех сильнейших спортсменов мира в каком-либо виде спорта, значит. проведено сплошное исследование. Все остальные исследования называются выборочными. Одной из основных характеристик выборки является ее объем – n, который определяется числом объектов наблюдения, например, спортсменов в данном исследовании. Как проводится упорядочение и анализ выборки? Предположим, что у баскетболистов измерили силу левой кисти. Результат измерений в килограммах (n = 100) представлен в таблице 2. Таблица 2 – Пример выборочных результатов (n = 100)
В этой таблице числа записаны в той последовательности, в какой проходили измерения, т.е. случайным образом. Такие данные представляют неупорядоченную выборку. Третья строка – выборка упорядоченная, точнее – ранжированная. Ранжированием называют расстановку результатов измерений в порядке возрастания или убывания. Выборки большого объема разбивают на интервалы. В простейшем случае их может быть два. Например, когда необходимо отобрать худших или лучших спортсменов. Однако, для получения достаточно точных результатов число интервалов (его обозначают буквой k) должно быть больше. В зависимости от объёма выборки количество интервалов устанавливают, придерживаясь формулы американского статистика Стерджесса:
На основании формулы Стерждесса требуемое число интервалов для разного объёма сведено в таблицу 3. Таблица 3 – Рекомендуемое число интервалов для выборки разного объема
Тогда величина, или шаг интервала, определяется:
где
На основе значений k и h заполняют таблицу 4. Таблица 4 – Вариационный ряд измерений
В столбец 1 записываем порядковые номера интервалов. Столбец 2 получают следующим образом: выбирают значение x (нижнюю границу 1-го интервала) равную Столбец 3 определяет частоту, или «встречаемость», значений выборки в каждом интервале. Она определяется числом результатов измерений, попавших в данный интервал. Под частостью понимают отношение частоты к общему числу элементов выборки (к ее объему). Сумма частот всех интервалов всегда равна объему выборок, а сумма частостей всех интервалов равна единице. Из этой таблицы можно определить, как часто каждое значение результатов измерений встречается в каждой выборке. Распределение, представленное в столбцах 2 и 3, в статистике называют вариационным рядом. Анализ вариационных рядов упрощается при графическом представлении. Рассмотрим основные графики вариационного ряда. 1. Полигон распределения (рис. 1). График строится в прямоугольной системе координат. Величины измеряемого показателя откладываются на оси абсцисс, частоты (частости) – на оси ординат.
Рисунок 1 – Полигон распределения (на оси абсцисс – середины интервалов, 2. Гистограмма распределения (рис. 2). График строится аналогично полигону распределения, однако на оси абсцисс откладываются не точки (середины интервалов), а отрезки, отображающие интервал, и вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам и интервалам.
36 41 46 51 56 61 66 71 76
Рисунок 2 – Гистограмма (на оси абсцисс – интервалы, на оси ординат – частоты) Меры центральной тенденции Центральную тенденцию выборки позволяют оценить такие статистические характеристики, как среднее арифметическое значение, мода, медиана. Наиболее просто получаемой мерой центральной тенденции является мода. Мода (Мо) – это такое значение в множестве наблюдений, которое встречается наиболее часто. В совокупности значений (2, 6, 6, 8, 7, 33, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения. В случае, когда все значения в группе встречаются одинаково часто, считают, что эта группа не имеет моды. Когда два соседних значения в ранжированном ряду имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды (например, в совокупности значений 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются 11 и 14); в таком случае группа измерений или оценок является бимодальной. Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот. Медиана (Me) – середина ранжированного ряда результатов измерений. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посередине между двумя центральными значениями, когда они упорядочены. Среднее арифметическое значение
где
Каждая из выше вычисленных мер центра является наиболее пригодной для использования в определенных условиях. Мода вычисляется наиболее просто – ее можно определить на глаз. Более того, для очень больших групп данных это достаточно стабильная мера центра распределения. Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления. Эта мера получается особенно легко в случае ранжированных данных. Среднее множество данных предполагает в основном арифметические операции. На величину среднего влияют значения всех результатов. Медиана и мода не требуют для определения всех значений. Посмотрим, что произойдет со средним, медианой и модой, когда удвоится максимальное значение в следующем множестве:
Множество 1: 1, 3, 3, 5, 6, 7, 8 33/7 5 3 Множество 2: 1, 3, 3, 5, 6, 7, 16 41/7 5 3
На величину среднего особенно влияют результаты, которые называют “выбросами”, т.е. данные, находящиеся далеко от центра группы оценок.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |


 (2.1)
(2.1) – максимальный результат измерений в выборке,
– максимальный результат измерений в выборке,  – минимальный результат. В рассматриваемом примере (табл. 2.1) для n = 100 принимаем k = 8. Шаг интервала
– минимальный результат. В рассматриваемом примере (табл. 2.1) для n = 100 принимаем k = 8. Шаг интервала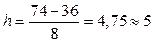 кг.
кг.

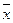 для неупорядоченного ряда измерений вычисляют по формуле:
для неупорядоченного ряда измерений вычисляют по формуле: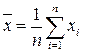 , (2.2)
, (2.2)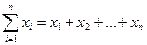 . Например, для данных 4,1; 4,4; 4,5; 4,7; 4,8 вычислим
. Например, для данных 4,1; 4,4; 4,5; 4,7; 4,8 вычислим  .
. Me Мо
Me Мо


