Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Число n называется размерностью линейного пространства V, а само пространство V называется n-мерным, если в V существует линейно независимая система из n векторов, а любая система из (n + 1)-го вектора линейно зависима. Размерность пространства Следствие. В n -мерном пространстве любая система из m векторов при m > n линейно зависима. Размерность линейного пространства V сокращенно обозначается Определение. Линейное пространство V называется бесконечномерным, если Теорема 3.2. Для того чтобы линейное пространство было n -мерным, необходимо и достаточно, чтобы в нем существовал базис, состоящий из n векторов. ► Достаточность. Дано: в пространстве V существует базис из n векторов ( Тогда в V есть линейно независимая система из n векторов (это система (3.27)). Покажем, что любая система из (n + 1)-го вектора в этом пространстве линейно зависима. Выберем одну из них: ( Каждый вектор системы (3.28) можно разложить по базису (3.27). Обозначим
(так как эта матрица имеет только n строк). По матричному критерию система (3.28) линейно зависима и, таким образом, Необходимость. Дано: ( одна из таких систем. Но ( линейно зависима. По 4-му свойству линейной зависимости (§ 2) вектор
Таким образом, (3.29) – система образующих пространства V, а значит, и его базис. ◄ Замечание. При доказательстве необходимости мы одновременно показали, что в n -мерном пространстве любая линейно независимая система из n векторов является базисом. Следствие. Любой базис конечномерного линейного пространства V содержит одинаковое количество векторов. ►Пусть в пространстве ( состоящий из m векторов (m ≠ n). Рассмотрим два случая: а) m > n. Тогда (3.31) линейно зависима согласно следствию к определению размерности, что противоречит определению базиса. б) m < n. Так как (3.31) – базис пространства Вывод: размерность линейного пространства совпадает с количеством векторов в любом из его базисов. Используя примеры базисов, приведенные в § 3, можно утверждать, что: Упражнение. Докажите, что Теорема 3.3. В n- мерном линейном пространстве любую линейно независимую систему из m векторов при m < n можно дополнить до базиса. ►Пусть
линейно независимая система пространства
линейно независима. Если m + 1 = n, то (3.33) – базис пространства
7. Определение. Пусть А – множество элементов произвольной природы, V – действительное линейное пространство. А называется аффинным пространством, связанным с линейным пространством V, если задан закон, по которому каждой паре элементов 1*. 2*. Элементы аффинного пространства называются точками, а операция в аффинном пространстве называется откладыванием вектора от точки.
Рис. 3.1 Рис. 3.2
Как видим, аксиомы аффинного пространства просто «списаны» со школьного точечного трехмерного пространства.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.007 с.) |

 по определению считается равной нулю.
по определению считается равной нулю. . Если
. Если  , то пространство будем обозначать
, то пространство будем обозначать  . Линейные n -мерные пространства называются конечномерными.
. Линейные n -мерные пространства называются конечномерными. в V найдется линейно независимая система из n векторов.
в V найдется линейно независимая система из n векторов. ). (3.27)
). (3.27) ). (3.28)
). (3.28) – координатные столбцы векторов системы (2) в базисе (1). Тогда
– координатные столбцы векторов системы (2) в базисе (1). Тогда
 .
.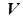 существует линейно независимая система из
существует линейно независимая система из  элементов. Пусть
элементов. Пусть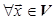 система
система ) (3.30)
) (3.30) можно представить в виде линейной комбинации векторов системы (3.29), т. е.
можно представить в виде линейной комбинации векторов системы (3.29), т. е.
 ), (3.31)
), (3.31) , поэтому система (3.29) линейно зависима, что противоречит определению базиса. Таким образом, m = n. ◄
, поэтому система (3.29) линейно зависима, что противоречит определению базиса. Таким образом, m = n. ◄ ,
,  ,
,  ,
,  ,
,  ,
,  . Примером бесконечномерного пространства может служить пространство всех функций.
. Примером бесконечномерного пространства может служить пространство всех функций. .
. – (3.32)
– (3.32) система
система  линейно зависима. Тогда на основании свойства 4º § 2, вектор
линейно зависима. Тогда на основании свойства 4º § 2, вектор  , что противоречит условию. Таким образом, найдется вектор
, что противоречит условию. Таким образом, найдется вектор  такой, что система
такой, что система – (3.33)
– (3.33)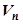 . В противном случае с системой (3.33) поступаем так же, как и с системой (3.32). После конечного числа шагов получаем базис пространства
. В противном случае с системой (3.33) поступаем так же, как и с системой (3.32). После конечного числа шагов получаем базис пространства  как пример аффинного, евклидова и метрического пространств.
как пример аффинного, евклидова и метрического пространств. , где
, где  , ставится в соответствие элемент
, ставится в соответствие элемент 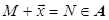 , причем выполняются две аксиомы.
, причем выполняются две аксиомы. (рис. 3.1).
(рис. 3.1). единственный
единственный  такой, что
такой, что  . Этот вектор обозначается
. Этот вектор обозначается  . Таким образом,
. Таким образом, 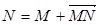 (рис. 3.2).
(рис. 3.2).