
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фрактальная размерность объектов гравитационного взаимодействияСодержание книги
Поиск на нашем сайте
Параметры Солнечной системы рассмотрим в следующей главе. Электрический и магнитный механизмы гравитации рассмотрены во Введении, п. 2. В п. 3.7 установлено равенство фрактальных размерностей Солнца и Галактики, ибо Галактика есть совокупность заряженных звезд типа Солнца. В п. 3.9 представлены фрактальные размерности планет Солнечной системы и Луны. В данном параграфе нас интересует фрактальная размерность заряженной материальной точки, которую определяют как отношение массы m заряженной материальной точки к ее заряду q в виде:
Такая запись правомерна при форме записи закона взаимодействия в системе СИ, где необходимо учитывать размерности массы (кг) и заряда (Кл) в этой системе единиц. Значение отношения, равное 4 Но в физике обратное отношение q/m = 1/4 Теперь приведем конкретные примеры определения параметров гравитационного взаимодействия Земли. Сила F, действующая на заряженную (заряд q) материальную точку, для общего случая определяется силой Лоренца и выражается в системе СИ в следующем виде [43]: F = qE + q[v • В]. (2.10) Первый член в (2.10) — сила, действующая на заряженную точку в электрическом поле Е, второй — в магнитном В. Так как F = m • g (см. п. 1.2 и [44]), то ускорение свободного падения Земли g определим, в соответствии с (2.10), исходя из справочных данных [6] для Е = 130 В/м. Однако возьмем более точное значение Е = 126 В/м, определенное из справочных данных заряда Земли, равного Q = -5,7 • 105Кл. Заметим, что электрическое поле и, соответственно, заряд Земли определяются зарядом Солнца. Итак, ускорение свободного падения на основании справочных данных определяется как g = qE/m = 126/4π = 10,0 м/с2, где принято m/q = 4π. Так как материальная точка и планета при взаимодействии одновременно вращаются вокруг оси планеты, то аналогом такого действия являются проводники с током разного направления, которые отталкиваются. Поэтому можно рассчитать, что среднее ускорение свободного падения g = 9,8 м/с2 (см. п. 3.5). Напомним, что противоположный заряд материальной точки, которая, может быть, является спутником, вызывается мгновенным действием электростатической индукции планеты через установленную структуру пространства [4]. Теперь на примере движения Луны, вызываемого зарядом Земли, рассчитаем ее скорость по орбите, как материальной точки. Исходя из ускорения Луны, связан-ного с радиусом круговой орбиты R и скоростью тела V, запишем формулу движения материальной точки (2.10) в электрическом поле в виде:
В данном расчете также принята размерность (см. (2.9)) для материальной точки, равная m/q = 4 Так как взаимодействующие объекты в пространстве имеют форму, то при определении силы взаимодействия их электрических и магнитных полей необходимо учитывать влияние размеров заряженных объектов. Заметим, традиционная физика не дала количественной теории определения взаимодействия заряженных форм: закон Кулона и сила Лоренца правомерны только для точечных зарядов. Поэтому автором проведены исследования по определению меры электрических и магнитных сил взаимодействующих заряженных форм. В результате исследований установлен закон взаимосвязи формы и электрического заряда (энергии). При этом учтено отличие электрических и магнитных полей. В отличие от магнитного поля электрическое поле действует не только на движущиеся, но и на покоящиеся заряды. Ввиду этого при определении силы взаимодействия заряженной сферы с электрическим полем необходимо делить ее на электрическую постоянную ε0 = 1/(36 электромагнитными силами вводится коэффициент пропорциональности действующая на заряженную сферу, равна F = qE/εo, а магнитная сила (см. (3.16)) F = Таким образом, суть закона взаимосвязи формы и энергии заключается в следующем: ток кок заряженные планеты и их спутники, звезды и центр Галактики имеют сферическую форму, то сила их взаимодействия с центральным объектом увеличивается по сравнению с точечным зарядом для электрических сил примерно на 11 порядков, а для магнитных сил — на 4 порядка. Следует констатировать неправомерность ядерной физики, которая объясняла всему миру принцип взрыва атомной бомбы наличием соответствующей критической массы радиоактивных веществ. Ведь в природе нет такого понятия, есть только закон взаимосвязи заряженных сферических форм и электрического заряда (энергии). Для примера рассмотрим определения магнитных полей планет с учетом их сферической формы. Для среднего магнитного поля планет в системе СИ получена [3] следующая формула:
((2.11) где = 36 Поясним значение полученных коэффициентов в формуле (2.11). В преобразовании 1/(4 плоскости. Коэффициент пропорциональности Тогда, исходя из справочных данных [6] для В = 4 = 53 • 10-6 Тл = 0,53 Гс. Мы знаем, что измеренное среднее значение магнитного поля Земли составляет около 0,5 Гс. Исходя из установленной поверхностной плотности заряда σ = -0,504 нКл/м2 планеты Юпитер [1, 2], рассчитаем его среднее магнитное поле: В = 4 На Юпитере обнаружено поле до 10 Гс [45], а на магнитнитном экваторе оно составляет 4,2 Гс [25]. Таким образом, среднее магнитное поле Юпитера близко к рассчетному. Значения плотности заряда и скорости осевого вращения планеты взяты из таблицы 3.1. Обратим внимание на объяснения происхождения магнитных полей этих планет, представленные в энциклопедических изданиях:
— «Происхождение магнитного поля Земли связыва — «Открытие магнитного поля Юпитера навело ас- Заметим: мы уже знаем [2], что никакого ядра в этих планетах не имеется; наличие ядра — это фикция, вызванная ложным законом тяготения Ньютона.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.01 с.) |

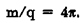 (2.9)
(2.9)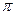 , является фрактальной размерностью материальной точки. Обратите внимание, что при определении размерности вихревого пространства (см. п. 2.3) учитывалась локальная размерность материальной точки как 4
, является фрактальной размерностью материальной точки. Обратите внимание, что при определении размерности вихревого пространства (см. п. 2.3) учитывалась локальная размерность материальной точки как 4 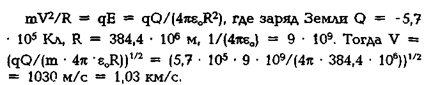
 0. Кроме того, при определении магнитных сил учитывается магнитная постоянная μ0 = 4
0. Кроме того, при определении магнитных сил учитывается магнитная постоянная μ0 = 4  , обусловленный рационализацией единицы заряда. Тогда электрическая сила (см. (3.18)),
, обусловленный рационализацией единицы заряда. Тогда электрическая сила (см. (3.18)),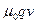 В/(
В/(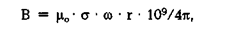
 — средняя поверхностная плотность отрицательного электрического заряда;
— средняя поверхностная плотность отрицательного электрического заряда; 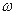 — угловая скорость осевого вращения; r — радиус планеты. В формуле (2.11) нормирующий коэффициент 1 • 109 получен из следующих преобразований коэффициентов 1/(4
— угловая скорость осевого вращения; r — радиус планеты. В формуле (2.11) нормирующий коэффициент 1 • 109 получен из следующих преобразований коэффициентов 1/(4  109/4
109/4 


