
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие скалярного произведенияСодержание книги
Поиск на нашем сайте Сначала про угол между векторами. Рассмотрим свободные ненулевые векторы Результат операции является ЧИСЛОМ: Умножается вектор на вектор, а получается число. Действительно, если длины векторов Пример 1. Найти скалярное произведение векторов Угол между векторами и значение скалярного произведения. Выясним, от чего зависит знак скалярного произведения. Смотрим на нашу формулу: 1) Если угол между векторами острый: 2) Если угол между векторами тупой: Справедливы и обратные утверждения: 1) Если 2) Если Но особый интерес представляет третий случай: 3) Если угол между векторами прямой: Скалярный квадрат вектора Вернёмся к ситуации, когда два вектора сонаправлены. В этом случае угол между ними равен нулю, А что будет, если вектор свойства скалярного произведения:Для произвольных векторов 1) 2) 3) Пример 3. Найти скалярное произведение векторов
Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора Пример 5 Найти длину вектора Решение будет следующим: (1) Поставляем выражение вектора (2) Используем формулу длины: (3) Используем школьную формулу квадрата суммы (4) Дальнейшее уже знакомо из двух предыдущих задач. Ответ: Коль скоро речь идёт о длине, не забываем указать размерность – «единицы». Пример 6 Найти длину вектора Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Угол между векторами Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу А части поменяем местами: В чём смысл данной формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол. Скалярное произведение Пример 7 Найти угол между векторами Решение: Используем формулу: Итак, если Значения обратных тригонометрических функций можно находить по тригонометрической таблице. Хотя случается это редко. В задачах аналитической геометрии значительно чаще появляется какой-нибудь неповоротливый медведь вроде Ответ: Опять, не забываем указывать размерность – радианы и градусы. Лично я, чтобы заведомо «снять все вопросы», предпочитаю указывать и то, и то (если по условию, конечно, не требуется представить ответ только в радианах или только в градусах). Теперь вы сможете самостоятельно справиться с более сложным заданием: Пример 7* Даны Задание даже не столько сложное, сколько многоходовое. 1) По условию требуется найти угол между векторами 2) Находим скалярное произведение 3) Находим длину вектора 4) Концовка решения совпадает с Примером №7 – нам известно число Краткое решение и ответ в конце урока. Второй раздел урока посвящен тому же скалярному произведению. Координаты. Будет даже проще, чем в первой части.
Скалярное произведение векторов, На уроке Векторы для чайников мы рассматривали два случая: векторы на плоскости и векторы в трехмерном пространстве, при этом «плоские» и «пространственные» формулы были весьма похожи. Для скалярного произведения векторов всё точно так же! Прежде чем продолжать дальше, скажу, что все рассмотренные выше утверждения, теоремы и задачи (первого раздела данной статьи) справедливы как для плоскости, так и для пространства. Второе важное замечание касается базиса. В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства. Повествование опять пойдёт параллельно – и для векторов плоскости и для пространственных векторов.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 и
и 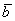 . Если отложить данные векторы от произвольной точки
. Если отложить данные векторы от произвольной точки  , то получится картинка
, то получится картинка Угол между векторами
Угол между векторами  может принимать значения от 0 до 180 градусов (от 0 до
может принимать значения от 0 до 180 градусов (от 0 до  радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства:
радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства:  либо
либо  (в радианах). Определение: Скалярным произведением двух векторов
(в радианах). Определение: Скалярным произведением двух векторов 
 или просто
или просто  .
. – это числа, косинус угла – число, то их произведение
– это числа, косинус угла – число, то их произведение  тоже будет числом.
тоже будет числом. Решение: Используем формулу
Решение: Используем формулу  . В данном случае:
. В данном случае:  Ответ:
Ответ:  .Чисто с математической точки зрения скалярное
.Чисто с математической точки зрения скалярное . Длины ненулевых векторов всегда положительны:
. Длины ненулевых векторов всегда положительны:  , поэтому знак может зависеть только от значения косинуса.Как уже отмечалось, угол между векторами может изменяться в пределах
, поэтому знак может зависеть только от значения косинуса.Как уже отмечалось, угол между векторами может изменяться в пределах  , и при этом возможны следующие случаи:
, и при этом возможны следующие случаи: (от 0 до 90 градусов), то
(от 0 до 90 градусов), то  , и скалярное произведение будет положительным:
, и скалярное произведение будет положительным:  . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым
. Особый случай: если векторы сонаправлены, то угол между ними считается нулевым  , и скалярное произведение также будет положительным. Поскольку
, и скалярное произведение также будет положительным. Поскольку  , то формула упрощается:
, то формула упрощается:  .
. (от 90 до 180 градусов), то
(от 90 до 180 градусов), то  , и, соответственно, скалярное произведение отрицательно:
, и, соответственно, скалярное произведение отрицательно:  . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым:
. Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым:  (180 градусов). Скалярное произведение тоже отрицательно, так как
(180 градусов). Скалярное произведение тоже отрицательно, так как 
 (90 градусов), то
(90 градусов), то  и скалярное произведение равно нулю:
и скалярное произведение равно нулю:  . Обратное тоже верно: если
. Обратное тоже верно: если 
 .
. умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой: 

 называется скалярным квадратом вектора
называется скалярным квадратом вектора  .Таким образом, скалярный квадрат вектора
.Таким образом, скалярный квадрат вектора

 и любого числа
и любого числа  справедливы следующие свойства:
справедливы следующие свойства: – переместительный или коммутативный закон скалярного произведения.
– переместительный или коммутативный закон скалярного произведения. – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки. – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения. и
и  , если известно, что
, если известно, что  . Решение: Сначала проясним ситуацию с вектором
. Решение: Сначала проясним ситуацию с вектором  и
и  . Так же с вектором
. Так же с вектором  – это сумма векторов
– это сумма векторов  .по условию требуется найти скалярное произведение
.по условию требуется найти скалярное произведение  .
. (1) Поставляем выражения векторов
(1) Поставляем выражения векторов  (2) Раскрываем скобки по правилу умножения многочленов.(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов:
(2) Раскрываем скобки по правилу умножения многочленов.(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов:  . Во 2ом слагаемом используем перестановочность скалярного произведения:
. Во 2ом слагаемом используем перестановочность скалярного произведения:  .(4) Приводим подобные слагаемые:
.(4) Приводим подобные слагаемые:  .(5) В первом слагаемом используем формулу скалярного квадрата
.(5) В первом слагаемом используем формулу скалярного квадрата  . Второе слагаемое раскладываем по стандартной формуле
. Второе слагаемое раскладываем по стандартной формуле  ,проводим окончательные вычисления. Ответ:
,проводим окончательные вычисления. Ответ:  Отрицательное значение - угол между векторами
Отрицательное значение - угол между векторами 
 , если
, если  .
.
 .
.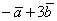 .
. . Обратите внимание, как она здесь любопытно работает:
. Обратите внимание, как она здесь любопытно работает:  – фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами:
– фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами:  – получилось то же самое с точностью до перестановки слагаемых.
– получилось то же самое с точностью до перестановки слагаемых.
 , если
, если  .
.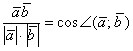

 – это число? Число. Длины векторов
– это число? Число. Длины векторов  тоже является некоторым числом
тоже является некоторым числом  . А если известен косинус угла:
. А если известен косинус угла:  , то с помощью обратной функции легко найти и сам угол:
, то с помощью обратной функции легко найти и сам угол:  .
. , если известно, что
, если известно, что  .
.
 .
. , то:
, то:
 , и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.
, и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.
 – длины векторов
– длины векторов  . Найти угол между векторами
. Найти угол между векторами  ,
,  .
. , поэтому нужно использовать формулу
, поэтому нужно использовать формулу  .
. (см. Примеры №№3,4).
(см. Примеры №№3,4). , а значит, легко найти и сам угол:
, а значит, легко найти и сам угол: 



