
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка векторов на ортогональность с помощью скалярного произведенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю: векторы Пример 9 а) Проверить ортогональность векторов: Решение: б) Здесь речь идёт об обычных отрезках плоскости (в чём сходство и различия вектора и отрезка, я очень подробно разъяснил на первом уроке). Речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы: Вычислим их скалярное произведение: Обратите внимание на два существенных момента: – В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю. – В окончательном выводе «между строк» подразумевается: «если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными». Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках: «значит, отрезки Ответ: а) Пример 10 Даны четыре точки пространства Это задача для самостоятельного решения. В условии требуется проверить перпендикулярность прямых. А решается задача снова через векторы по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно – если удастся доказать перпендикулярность векторов, то из этого автоматически будет следовать перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых. Полное решение и ответ в конце урока. Мощь аналитической геометрии – в векторах. Так, в рассмотренных примерах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета. Завершая разговор об ортогональности, разберу ещё одну небольшую задачу, которая время от времени встречается на практике:
Пример 11 При каком значении Решение: По условию требуется найти такое значение параметра Дело за малым, составим уравнение: Раскрываем скобки и приводим подобные слагаемые: Решаем простейшее линейное уравнение: Ответ: при В рассмотренной задаче легко выполнить проверку, в исходные векторы И находим скалярное произведение: Пример 12 При каком значении Это простенький пример с векторами плоскости. Для самостоятельного решения. Немного усложним задачу:
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.153.251 (0.01 с.) |

 и
и  ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 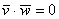 . В координатах данный факт запишется следующим образом:
. В координатах данный факт запишется следующим образом: (для векторов плоскости);
(для векторов плоскости); (для векторов пространства).
(для векторов пространства). и
и 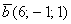
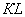 и
и 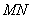 , если
, если 
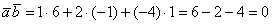 , следовательно,
, следовательно, 
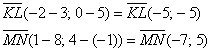
 , значит, отрезки
, значит, отрезки 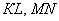 не перпендикулярны.
не перпендикулярны. . Выяснить будут ли перпендикулярными следующие прямые:
. Выяснить будут ли перпендикулярными следующие прямые: ;
; .
. векторы
векторы  будут ортогональны?
будут ортогональны? ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда  .
.
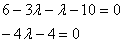


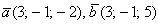
 – да, действительно, при
– да, действительно, при  ортогональны, что и требовалось проверить.
ортогональны, что и требовалось проверить. будет равно –2?
будет равно –2?


