
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия с векторами в координатахСодержание книги
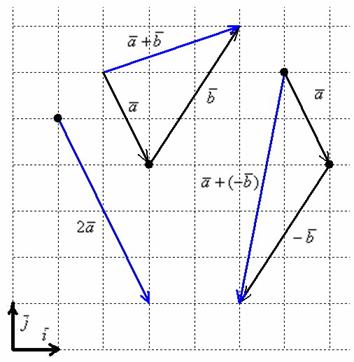
Поиск на нашем сайте В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов: 1) Правило сложения векторов. Рассмотрим два вектора плоскости Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор Для пространственного вектора Приведённые факты строго доказываются в курсе аналитической геометрии. Примечание: Данные правила справедливы не только для ортонормированных базисов Пример 7 Даны векторы Решение чисто аналитическое: Ответ: Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать, что векторы заданы в ортонормированном базисе Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости. Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо): Пример 8 Даны векторы Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем: Ответ: И в заключение занятный пример с векторами на плоскости: Пример 9 Даны векторы Это задача для самостоятельного решения. Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки: !!! Скалярное произведение векторов Это, так скажем, вектор-минимум студента =) Любите векторы, и векторы полюбят вас! Решения и ответы: Задание: Пример 2: Решение: Пример 4: Решение:
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

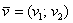 и
и  . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:  . Как просто. На всякий случай запишу частный случай – формулу разности векторов:
. Как просто. На всякий случай запишу частный случай – формулу разности векторов:  . Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор
. Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор 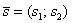 и найдём сумму трёх векторов:
и найдём сумму трёх векторов: 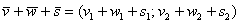
 , то их суммой является вектор
, то их суммой является вектор  .
. , необходимо каждую координату данного вектора умножить на число
, необходимо каждую координату данного вектора умножить на число  .
.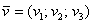 правило такое же:
правило такое же:
 ,
, 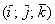 но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов.
но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов. и
и 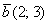 . Найти
. Найти 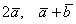 и
и 


 и
и  . Найти
. Найти  и
и 

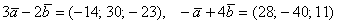
 . Найти
. Найти  и
и 
 ,
, 


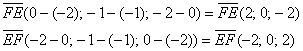

 и
и 





