
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Очевидно, что при перемещении вектора его проекция не меняетсяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вспомним школу. Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае: С другой стороны, у нас уже получена формула косинуса угла между векторами: Таким образом: Сокращаем знаменатели обеих частей на Формула выведена, распишем её в координатах: Если векторы плоскости Если векторы пространства Пример 18 Найти проекцию вектора Решение в одну строчку: Ответ: Проекция – это ДЛИНА, поэтому обязательно указываем размерность. Длина, конечно, своеобразная, в случае тупизны угла между векторами к ней добавляется знак «минус». В задачах приходится находить не только проекцию вектора на вектор, но и проекцию отрезка на отрезок, отрезка на прямую и т.д. Но, так или иначе, в решении используются векторы! Пример 19 Треугольник задан своими вершинами Это задача для самостоятельного решения. Решение и ответ в конце урока. Выясним геометрический смысл координат векторов в ортонормированном базисе: Проекция вектора на координатные оси. Рассмотрим вектор плоскости
Проекцией вектора Аналогично со второй координатой: проекцией вектора Косинусы Заметьте, что приведённые выше выкладки не изменятся, если вектор Итак, координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси). Направляющие косинусы ненулевого вектора Кроме того, вектор с координатами из соответствующих направляющих косинусов: – коллинеарен исходному вектору «вэ»; – его длина равна единице (так называемый единичный вектор). С пространственными векторами, заданными в ортонормированном базисе В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример урока: Пример 20 Найти направляющие косинусы векторов: Простая задача для самостоятельного решения. Фактически, она состоит в том, чтобы найти длину векторов и составить эти самые направляющие косинусы. Однако не забывайте, что вместе с направляющими косинусами нам автоматически становятся известными единичные векторы, которые коллинеарны векторам «а» и «бэ». К слову, практическая задача на нахождения единичного вектора рассмотрена в Примере №5 урока Уравнение плоскости. Ну а здесь решение и ответ совсем близко. После изучения данного урока, у вас уже весьма приличная подготовка по аналитической геометрии. Чтобы паззл сложился окончательно, читайте статьи Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. Любите векторы, и векторы полюбят вас! Решения и ответы: Пример 2: Решение: Пример 4: Решение: Пример 6: Решение: Пример 7*: Решение: Используем формулу Пример 10: Решение: Пример 12: Решение: Составим и решим уравнение: Пример 14: Решение: Пример 17: Решение: Найдем векторы Пример 19: Решение: Найдём векторы: Пример 20: Решение: Ответ: Автор: Емелин Александр Линейная зависимость и линейная независимость векторов.
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой. Линейная зависимость векторов, линейная независимость векторов, базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, абстрактный алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) носят общий алгебраический смысл, но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания линейной алгебры. Для освоения материала желательно прочитать статьи Векторы для чайников и Как вычислить определитель?
Линейная зависимость и независимость векторов плоскости. Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях: 1) Выбрать базис плоскости. Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка. 2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам. Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор Картинку сего действа можно посмотреть на уроке Векторы для чайников, где я объяснял правило умножения вектора на число. Будут ли ваши пальчики Такие векторы называют линейно зависимыми. Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-ой степени) выражения и зависимости. Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны. Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости Любой вектор плоскости Также говорят, что вектор Например, можно сказать, что вектор Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат: Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом
Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости. С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис Точка Думаю, всем понятно, что с помощью точки Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку
! Примечание: в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ. Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры». И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными. Соответственно угол может быть любым, кроме 0 и 180 градусов. Точка
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников, многие вкусные формулы, связанные со скалярным произведением векторов. Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении, а также ещё некоторые типы задач, которые мы скоро рассмотрим. А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.009 с.) |




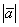 и получаем формулу для вычисления проекции:
и получаем формулу для вычисления проекции:
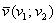 и
и  , заданы в ортонормированном базисе
, заданы в ортонормированном базисе  , то проекция вектора
, то проекция вектора  на вектор
на вектор 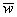 выражается формулой:
выражается формулой: .
. , заданы в ортонормированном базисе
, заданы в ортонормированном базисе 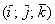 , то проекция вектора
, то проекция вектора 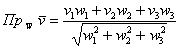
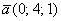 на вектор
на вектор 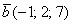


 . Найти:
. Найти: на сторону
на сторону  ;
; , заданный своими координатами в ортонормированном базисе
, заданный своими координатами в ортонормированном базисе 
 на координатную ось
на координатную ось  является в точности его первая координата:
является в точности его первая координата: 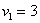 (красная черта). Обозначим через
(красная черта). Обозначим через  угол между вектором
угол между вектором  :
:  (красная дуга). Тогда:
(красная дуга). Тогда: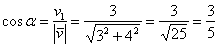 (определение косинуса в прямоугольном треугольнике недавно упоминалось).
(определение косинуса в прямоугольном треугольнике недавно упоминалось). является его вторая координата:
является его вторая координата:  (малиновая черта). Обозначим через
(малиновая черта). Обозначим через  угол между вектором
угол между вектором  :
:  (двойная малиновая дуга). Тогда:
(двойная малиновая дуга). Тогда:
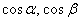 называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство
называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство  . Проверим его справедливость для рассматриваемого вектора:
. Проверим его справедливость для рассматриваемого вектора: , что и требовалось проверить.
, что и требовалось проверить. , а сами координаты вектора можно выразить через его длину и данные косинусы:
, а сами координаты вектора можно выразить через его длину и данные косинусы:  , то есть:
, то есть:  .
. . Его координаты представляют собой проекции вектора на оси
. Его координаты представляют собой проекции вектора на оси  соответственно. Обозначим углы данного вектора с ортами через:
соответственно. Обозначим углы данного вектора с ортами через:  . Тогда направляющие косинусы вектора выражаются формулами:
. Тогда направляющие косинусы вектора выражаются формулами:  , и справедливым является равенство
, и справедливым является равенство  .
.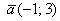 , проверить, что
, проверить, что  , проверить, что
, проверить, что 


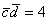


 .
. 
 :
: 
 :
: 



 , значит, прямые
, значит, прямые  не перпендикулярны.
не перпендикулярны. 
 , значит, прямые
, значит, прямые  перпендикулярны.
перпендикулярны. 












 .
.  .
.  , что и требовалось проверить.
, что и требовалось проверить.  .
.  .
.  , что и требовалось проверить.
, что и требовалось проверить.
 . Или вектор погоды, за которым я только что сходил на Гисметео:
. Или вектор погоды, за которым я только что сходил на Гисметео: 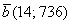 – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
– температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени…. . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор
. Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор  . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах
. Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах  ? Данные векторы коллинеарны, а значит, линейно выражаются друг через друга:
? Данные векторы коллинеарны, а значит, линейно выражаются друг через друга: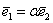 , ну, или наоборот:
, ну, или наоборот:  , где
, где 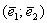 получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы , где
, где  – действительные числа. Числа
– действительные числа. Числа  называют разложением вектора
называют разложением вектора 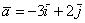 разложен по ортонормированному базису плоскости
разложен по ортонормированному базису плоскости  .
. – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
– это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
 плоскости, которая называется началом координат, и ортонормированный базис
плоскости, которая называется началом координат, и ортонормированный базис 
 или
или  . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
. Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.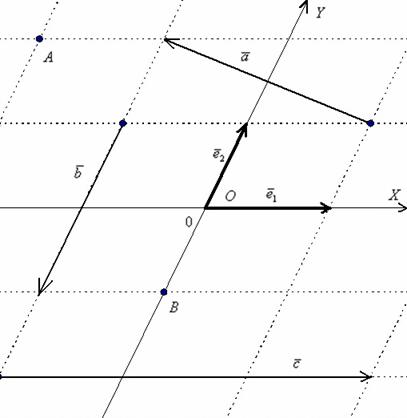
 и векторы:
и векторы:



