
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула косинуса угла между векторами, которые заданы координатамиСодержание книги
Поиск на нашем сайте
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами Косинус угла между векторами плоскости Косинус угла между векторами пространства Пример 16 Даны три вершины треугольника Решение: По условию чертёж выполнять не требуется, но всё-таки: Из чертежа совершенно очевидно, что угол Проведённый анализ желательно научиться выполнять мысленно. Найдём векторы: Вычислим скалярное произведение: И длины векторов: Косинус угла: Именно такой порядок выполнения задания рекомендую чайникам. Более подготовленные читатели могут записывать вычисления «одной строкой»: Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе. Найдём сам угол: Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки угол также можно измерить и транспортиром. Не повредите покрытие монитора =) Ответ: В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем указать точный ответ: Те, кто получил удовольствие от процесса, могут вычислить углы Пример 17 В пространстве задан треугольник координатами своих вершин Это пример для самостоятельного решения. Полное решение и ответ в конце урока Небольшой заключительный раздел будет посвящен проекциям, в которых тоже «замешано» скалярное произведение:
Проекция вектора на вектор. Проекция вектора на координатные оси. Рассмотрим векторы
Данное ЧИСЛО обозначается следующим образом: Сама запись Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ». Если угол между векторами Если векторы Если угол между векторами Отложим данные векторы от одной точки:
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 791; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.58.68 (0.006 с.) |

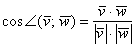 выразить через координаты векторов
выразить через координаты векторов  :
: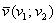 и
и  , заданными в ортонормированном базисе
, заданными в ортонормированном базисе  , выражается формулой:
, выражается формулой: .
. , заданными в ортонормированном базисе
, заданными в ортонормированном базисе 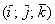 , выражается формулой:
, выражается формулой: 
 . Найти
. Найти  (угол при вершине
(угол при вершине  ).
).
 .
. и
и  , иными словами:
, иными словами:  .
.


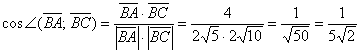
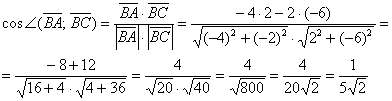
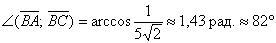

 и приближенное значение угла:
и приближенное значение угла:  , найденное с помощью калькулятора.
, найденное с помощью калькулятора.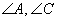 , и убедиться в справедливости канонического равенства
, и убедиться в справедливости канонического равенства 
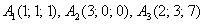 . Найти угол между сторонами
. Найти угол между сторонами  и
и 
 и
и 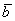 :
:
 (красная линия) будет «тенью» вектора
(красная линия) будет «тенью» вектора  , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
, «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.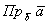 читается так: «проекция вектора «а» на вектор «бэ»».
читается так: «проекция вектора «а» на вектор «бэ»». острый (как на рисунке), то
острый (как на рисунке), то 
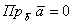 (проекцией является точка, размеры которой считаются нулевыми).
(проекцией является точка, размеры которой считаются нулевыми). ), то
), то  (та же длина, но взятая со знаком минус).
(та же длина, но взятая со знаком минус).



