
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как построить точку, симметричную относительно прямой?Содержание книги
Поиск на нашем сайте
Задача состоит в том, чтобы найти координаты точки 1) Находим прямую 2) Находим точку пересечения прямых: Оба действия подробно разобраны в рамках данного урока. 3) Точка Не лишним будет проверить, что расстояние Трудности здесь могут возникнуть в вычислениях, но в вышке здорово выручает микрокалькулятор, позволяющий считать обыкновенные дроби. Неоднократно советовал, посоветую и снова. Как найти расстояние между двумя параллельными прямыми? Пример 9 Найти расстояние Это очередной пример для самостоятельного решения. Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце урока, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать. Угол между двумя прямыми Что ни угол, то косяк: Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4-х углов. Чем отличаются углы Зачем я это рассказал? Вроде бы можно обойтись и обычным понятием угла. Дело в том, что в формулах, по которым мы будем находить углы, запросто может получиться отрицательный результат, и это не должно застать вас врасплох. Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке). Как найти угол между двумя прямыми? Существуют две рабочие формулы: Пример 10 Найти угол между прямыми Решение и Способ первый Рассмотрим две прямые, заданные уравнениями в общем виде: Если прямые не перпендикулярны, то ориентированный угол Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых: Если Исходя из вышесказанного, решение удобно оформить в два шага: 1) Вычислим скалярное произведение направляющих векторов прямых: 2) Угол между прямыми найдём по формуле:
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса (см. Графики и свойства элементарных функций): Ответ: В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора. Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация: Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты Утаивать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того. Для проверки решения можно взять транспортир и измерить угол. Способ второй Если прямые заданы уравнениями с угловым коэффициентом Условие перпендикулярности прямых выражается равенством Алгоритм решения похож на предыдущий пункт. Но сначала перепишем наши прямые в нужном виде: Таким образом, угловые коэффициенты: 1) Проверим, будут ли прямые перпендикулярны: 2) Используем формулу: Ответ: Второй способ уместно использовать тогда, когда уравнения прямых изначально заданы с угловым коэффициентом. Следует отметить, что если хотя бы одна прямая параллельна оси ординат, то формула не применима вообще, поскольку для таких прямых угловой коэффициент не определён (см. статью Уравнение прямой на плоскости). Есть и третий способ решения. Идея состоит в том, чтобы вычислить угол между направляющими векторами прямых с помощью формулы, рассмотренной на уроке Скалярное произведение векторов: Здесь уже речь идёт не об ориентированном угле, а «просто об угле», то есть результат заведомо будет положительным. Загвоздка состоит в том, что может получиться тупой угол (не тот, который нужен). В этом случае придётся делать оговорку, что угол между прямыми – это меньший угол, и из «пи» радиан (180-ти градусов) вычитать получившийся арккосинус. Желающие могут прорешать задачу третьим способом. Но я рекомендую всё-таки придерживаться первого подхода с ориентированным углом, по той причине, что он широко распространён. Пример 11 Найти угол между прямыми Это пример для самостоятельного решения. Попробуйте решить его двумя способами. Как-то заглохла по ходу дела сказка…. Потому что нет никакого Кащея Бессмертного. Есть я, причём, не особо запаренный. Если честно, думал, статья значительно длиннее выйдет. Но все равно возьму недавно приобретенную шапочку с очками и пойду купаться в сентябрьской озёрной воде. Отлично снимает усталость и негативную энергетику. До скорых встреч! И помните, Бабу-Ягу никто не отменял =) Решения и ответы: Пример 3: Решение: Найдём направляющий вектор прямой Пример 5: Решение: Пример 7: Решение: Пример 9: Решение: Расстояние между параллельными прямыми найдём как расстояние от точки до прямой. Для этого достаточно найти одну точку, принадлежащую любой из прямых. В целях удобного подбора точки перепишем уравнение Пример 11: Решение: Автор: Емелин Александр
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.007 с.) |

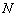 , которая симметрична точке
, которая симметрична точке 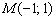 относительно прямой
относительно прямой  . Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:
. Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами: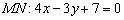 , которая перпендикулярна прямой
, которая перпендикулярна прямой  .
.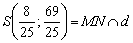 .
.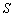 является серединой отрезка
является серединой отрезка 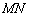 . Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим
. Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим  .
. тоже равно 2,2 единицам.
тоже равно 2,2 единицам.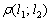 между двумя параллельными прямыми
между двумя параллельными прямыми 
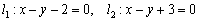
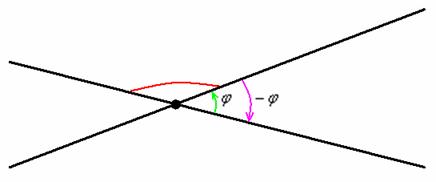
 или противоположно ориентированный «малиновый» угол
или противоположно ориентированный «малиновый» угол  .
. ? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если
? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если 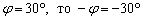 .
.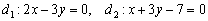


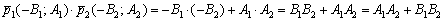
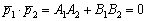 , то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.
, то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке. , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.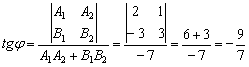
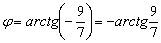

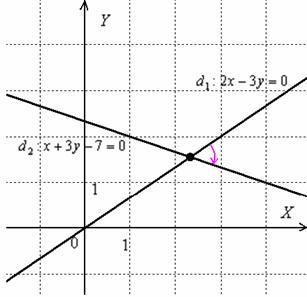
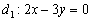 и «открутка» угла началась именно с неё.
и «открутка» угла началась именно с неё.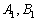 взять из второго уравнения
взять из второго уравнения 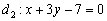 , а коэффициенты
, а коэффициенты 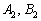 взять из первого уравнения
взять из первого уравнения  и не перпендикулярны, то ориентированный угол
и не перпендикулярны, то ориентированный угол 
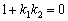 , откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых:
, откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых: 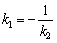 , которая используется в некоторых задачах.
, которая используется в некоторых задачах.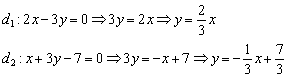

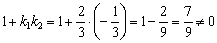 , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.
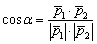
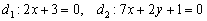 .
.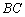 :
: 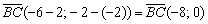
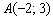 и направляющему вектору
и направляющему вектору 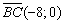 . Так как одна из координат направляющего вектора нулевая, уравнение
. Так как одна из координат направляющего вектора нулевая, уравнение 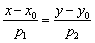 перепишем в виде:
перепишем в виде: 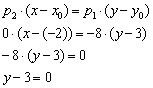

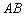 составим по двум точкам
составим по двум точкам  :
: 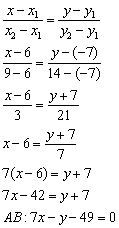
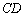 составим по двум точкам
составим по двум точкам 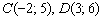 :
: 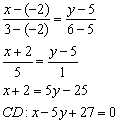
 не пропорциональны:
не пропорциональны: 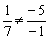 , значит, прямые пересекаются.
, значит, прямые пересекаются.  :
: 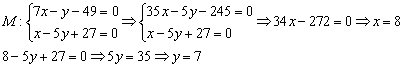
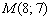
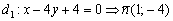 .
. 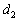 по точке
по точке  и направляющему вектору
и направляющему вектору  :
: 
 :
: 

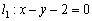 в виде уравнения с угловым коэффициентом:
в виде уравнения с угловым коэффициентом: 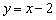 . Точка
. Точка  . Вычислим расстояние:
. Вычислим расстояние: 
 – чтобы избавиться от иррациональности в знаменателе.
– чтобы избавиться от иррациональности в знаменателе. 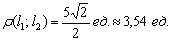
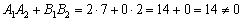 , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны. 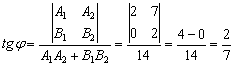


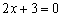 параллельна оси ординат, и её угловой коэффициент не определён.
параллельна оси ординат, и её угловой коэффициент не определён.


