Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектор нормали плоскости (нормальный вектор)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного. Обещанного три экрана ждут, вернёмся к Примеру №1 и выполним его проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке Во-первых, подставим координаты точки Во-вторых, из уравнения плоскости снимаем вектор нормали: Вывод: уравнение плоскости найдено правильно. В ходе проверки я фактически процитировал следующее утверждение теории: вектор Решим важную задачу, которая имеет отношение и к уроку Скалярное произведение векторов: Пример 5 Найти единичный нормальный вектор плоскости Решение: Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через Сначала из уравнения плоскости снимем вектор нормали: Как найти единичный вектор? Для того чтобы найти единичный вектор Перепишем вектор нормали в виде Согласно вышесказанному: Ответ: Проверка: Читатели, которые внимательно изучили последний параграф урока Скалярное произведение векторов, наверное, заметили, что координаты единичного вектора Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор, и по условию требуется найти его направляющие косинусы (последние задачи урока Скалярное произведение векторов), то вы, по сути, находите и единичный вектор, коллинеарный данному. Фактически два задания в одном флаконе. Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа. С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |


 , то вектор
, то вектор  является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.
является вектором нормали данной плоскости. Просто до безобразия. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.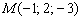 и двум векторам
и двум векторам  . В результате решения мы получили уравнение
. В результате решения мы получили уравнение 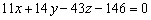 . Проверяем:
. Проверяем:
 действительно лежит в данной плоскости.
действительно лежит в данной плоскости. . Поскольку векторы
. Поскольку векторы  перпендикулярен плоскости, то должны иметь место следующие факты:
перпендикулярен плоскости, то должны иметь место следующие факты:  . Перпендикулярность векторов легко проверить с помощью скалярного произведения:
. Перпендикулярность векторов легко проверить с помощью скалярного произведения:
 параллелен плоскости
параллелен плоскости  .
. .
. . Принципиально пейзаж выглядит так:
. Принципиально пейзаж выглядит так: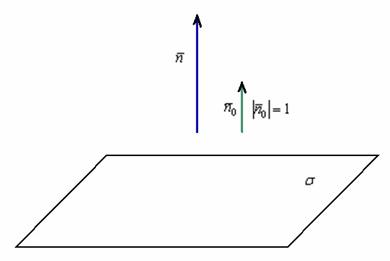
 коллинеарны.
коллинеарны. .
. разделить на длину вектора
разделить на длину вектора  .
. и найдём его длину:
и найдём его длину:


 , что и требовалось проверить.
, что и требовалось проверить.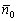 – это в точности направляющие косинусы вектора
– это в точности направляющие косинусы вектора