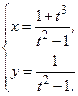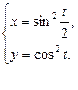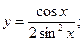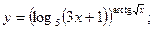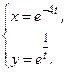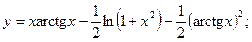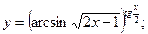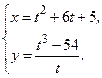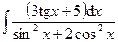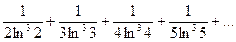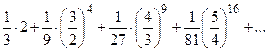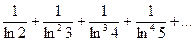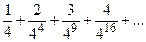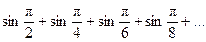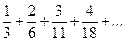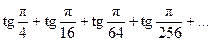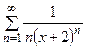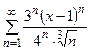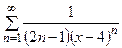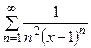Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Элементы линейной и векторнойСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ Курс математики является фундаментом образования студента, имеющим большое значение не только для изучения общетехнических дисциплин, но и для специальных дисциплин в особенности. Цель преподавания математики состоит в том, чтобы ознакомить студентов с основами математического аппарата, необходимого для решения как теоретических, так и практических задач; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных задач и умение сформулировать задачи по специальности на математическом языке. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых — оказать студенту помощь в его работе. Рецензии на контрольные задания позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него проблемы, на желательное направление дальнейшей работы. При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. 1. Каждая работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного и зеленого. Необходимо оставлять поля шириной 4─5 см, для замечаний рецензента. 2. В заголовке на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента. 3. Решение задач надо располагать в порядке возрастания их номеров, указанных в заданиях. 4. Перед решением каждой задачи надо полностью написать ее условие. 5. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 6. После полученной прорецензированной контрольной работы, как недопущенной, так и допущенной к собеседованию, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. ПРОГРАММА КУРСА
Раздел 1. Элементы линейной и векторной Алгебры 1. Матрицы (основные понятия). Линейные операции над матрицами, их свойства. 2. Умножение матриц. Свойства умножения. 3. Определители 2-го и 3-го порядков. Понятие определителя n -го порядка. 4. Миноры, алгебраические дополнения. Теорема о разложении определителя по элементам ряда. 5. Свойства определителей. 6. Обратная матрица. Необходимое и достаточное условия существования обратной матрицы. 7. Системы линейных уравнений. Основные определения. Матричная запись. 8. Невырожденные системы. Формулы Крамера. Метод Гаусса. 9. Ранг матрицы. Теорема об инвариантности ранга матрицы. 10. Теорема Конекера─Капелли. Решение произвольных систем. 11. Системы однородных линейных уравнений. 12. Понятие вектора. Линейные операции над векторами. 13. Базис и координаты вектора. 14. Прямоугольная система координат. Линейные операции над векторами в линейной форме. 15. Скалярное произведение векторов: его свойства. 16. Векторное произведение векторов: его свойства. 17. Смешанное произведение векторов: его свойства. 18. Необходимое и достаточное условия компланарности векторов.
Раздел 2. Аналитическая геометрия 1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости. Уравнение плоскости в отрезках. 2. Уравнение плоскости, проходящей через три точки. 3. Нормальное уравнение плоскости. Расстояние от точки до плоскости. 4. Взаимное расположение плоскостей. Угол между плоскостями. 5. Канонические и параметрические уравнения прямой. Уравнение прямой, проходящей через две точки. 6. Сведение общего уравнения прямой в пространстве к каноническим уравнениям. 7. Способы задания прямой на плоскости: а) прямая, проходящая через точку перпендикулярно данному вектору; б) общее уравнение; в) уравнение в отрезках; г) уравнение прямой с угловым коэффициентом; д) уравнение прямой, проходящей через точку в данном направлении. 8. Взаимное расположение прямых на плоскости. Угол между прямыми. 9. Нормальное уравнение прямой. Расстояние от точки до прямой. 10. Взаимное расположение прямых в пространстве. Угол между прямыми. 11. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. 12. Эллипс (определение, каноническое уравнение, исследование формы). 13. Гипербола (определение, каноническое уравнение, исследование формы). 14. Парабола (определение, каноническое уравнение, исследование формы). 15. Исследование общего уравнения линии второго порядка в случае отсутствия члена с произведением текущих координат. 16. Поверхности второго порядка.
Раздел 3. Введение в математический анализ
1. Числовая последовательность и ее предел. 2. Теорема об ограниченности сходящейся последовательности. Теорема Вейерштрасса. 3. Предел функции при x ® a и при x ®¥. Односторонние пределы. 4. Бесконечно большие и бесконечно малые функции. Связь между ними. 5. Свойства бесконечно малых функций. 6. Теорема о разложении функции, имеющей предел, на постоянную и бесконечно малую функцию. 7. Теорема об единственности предела функции. Предел суммы, произведения и частного функций. 8. Первый замечательный предел. 9. Второй замечательный предел. 10. Сравнение бесконечно малых. Эквивалентные бесконечно малые. 11. Теоремы об эквивалентных бесконечно малых. 12. Непрерывность функции в точке. Действия над непрерывными функциями. 13. Классификация точек разрыва. 14. Односторонняя непрерывность. Свойства непрерывных на отрезке функций.
Раздел 4. Дифференциальное исчисление функции Одной переменной
1. Производная. Геометрический и механический смысл. 2. Теорема о непрерывности дифференцируемой функции. 3. Основные правила дифференцирования. 4. Производная сложной функции. 5. Производные основных и элементарных функций. 6. Производная функции, заданной неявно. 7. Производная функции, заданной параметрически. 8. Логарифмическое дифференцирование. 9. Производные высших порядков. 10. Дифференциал функции, его свойства, геометрический смысл. 11. Применение дифференциала в приближенных вычислениях. 12. Дифференциалы высших порядков. 13. Теоремы Ролля, Лагранжа, Коши. 14. Раскрытие неопределенностей вида 15. Раскрытие неопределенностей других видов по правилу Лопиталя. 16. Экстремумы функции. Необходимое условие экстремума (теорема Ферма). 17. Достаточное условие возрастания (убывания) функции. 18. Достаточные условия существования экстремума. 19. Выпуклость, вогнутость графика функции; достаточные условия. 20. Точки перегиба графика функции; достаточные условия. 21. Асимптоты графика функции. 22. Общая схема исследования функции и построения графика. 23. Наименьшее и наибольшее значения непрерывной на отрезке функции.
Интегралы 1. Двойной интеграл; его основные свойства. 2. Вычисление двойного интеграла в декартовых координатах. 3. Вычисление двойного интеграла в полярных координатах. 4. Тройной интеграл; его основные свойства. 5. Вычисление тройного интеграла в декартовых координатах. 6. Вычисление тройного интеграла в цилиндрических. 7. Приложение кратных интегралов к решению задач в геометрии. 8. Приложение кратных интегралов к решению задач механики. 9. Криволинейные интегралы первого рода; их свойства и вычисление. 10. Криволинейные интегралы второго рода; их свойства и вычисление. 11. Поверхностные интегралы первого рода; их свойства и вычисление. 12. Поверхностные интегралы второго рода; их свойства и вычисление.
Раздел 11. Ряды 1. Числовой ряд. Сумма и остаток ряда. 2. Необходимый признак сходимости ряда. 3. Сравнение рядов с положительными членами. 4. Достаточные признаки сходимости Даламбера и Коши. 5. Интегральный признак Коши. 6. Знакочередующиеся ряды. Признак Лейбница. 7. Знакопеременные ряды. Абсолютная и условная сходимость. 8. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости. 9. Свойства степенных рядов. 10. Ряды Тейлора и Маклорена. 11. Разложение функций sin x, cos x, ex, ln(1 ± x), (1 + x) m в ряды Маклорена. 12. Применение степенных рядов в приближенных вычислениях. Учебники
1. Герасимович, А.И., Рысюк, Н.А. Математический анализ. Ч.1.-Мн.: Выш. шк., 1989. 2. Герасимович, А.И., Кеда, Н.П., Сугак, М.Б. Математический анализ.Ч.2.-Мн.: Выш. шк., 1990. 3. Гурский, Е.И. Основы линейной алгебры и аналитической геометрии. -Мн.: Выш. шк., 1982. 4. Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.1. 5. Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.2. 6. Письменный, Д. Конспект лекций по высшей математике. 1часть.-М., Айрис Пресс,2004. 7. Письменный, Д. Конспект лекций по высшей математике. 2часть.-М., Айрис Пресс,2004.
Задачники 8. Гурский, Е.И. Руководство к решению задач по высшей математике. В 2ч. -Мн.: Выш. шк., 1989. Ч.1. 9. Гурский, Е.И. Руководство к решению задач по высшей математике. В 2 ч. -Мн.: Выш. шк., 1990. Ч.2. 10. Данко, П.Е., Попов, А.Г., Кожевникова, Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., ч.1. -М., Высш. шк., 1986, 1997, 1999. 11. Данко, П.Е., Попов, А.Г., Кожевникова, Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., Ч.2.-М., Высш. шк., 1986, 1997, 1999. 12. Сухая, Т.А., Бубнов, В.Ф. Задачи по высшей математике. В 2 ч., ч.1-Мн.: Выш. школа, 1993. 13. Сухая, Т.А., Бубнов, В.Ф. Задачи по высшей математике. В 2 ч., ч.2.-Мн.: Выш. школа, 1993. 14. Индивидуальные задания по высшей математике (под ред. Рябушко, А.П.). В 3 ч. -Мн.: Выш. шк., 2000. 15. Рябушко, А.П. Индивидуальные задания по высшей математике. Мн.: Выш. шк., 2006.
З А Д А Н И Я Д Л Я К О Н Т Р О Л Ь Н Ы Х Р А Б О Т Функции одной переменной Задания 51─60. Найти производные
52.
53.
54.
55.
56.
57.
58.
59.
60.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
Раздел 11. Ряды
Задания 161–170. Записать общий член ряда и исследовать ряд на сходимость.
161.
162. 163.
164. 165.
166.
167.
168.
169.
170.
Задания 171–180. Найти область сходимости следующих рядов:
ВВЕДЕНИЕ Курс математики является фундаментом образования студента, имеющим большое значение не только для изучения общетехнических дисциплин, но и для специальных дисциплин в особенности. Цель преподавания математики состоит в том, чтобы ознакомить студентов с основами математического аппарата, необходимого для решения как теоретических, так и практических задач; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных задач и умение сформулировать задачи по специальности на математическом языке. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых — оказать студенту помощь в его работе. Рецензии на контрольные задания позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него проблемы, на желательное направление дальнейшей работы. При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. 1. Каждая работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного и зеленого. Необходимо оставлять поля шириной 4─5 см, для замечаний рецензента. 2. В заголовке на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента. 3. Решение задач надо располагать в порядке возрастания их номеров, указанных в заданиях. 4. Перед решением каждой задачи надо полностью написать ее условие. 5. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 6. После полученной прорецензированной контрольной работы, как недопущенной, так и допущенной к собеседованию, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. ПРОГРАММА КУРСА
Раздел 1. Элементы линейной и векторной Алгебры 1. Матрицы (основные понятия). Линейные операции над матрицами, их свойства. 2. Умножение матриц. Свойства умножения. 3. Определители 2-го и 3-го порядков. Понятие определителя n -го порядка. 4. Миноры, алгебраические дополнения. Теорема о разложении определителя по элементам ряда. 5. Свойства определителей. 6. Обратная матрица. Необходимое и достаточное условия существования обратной матрицы. 7. Системы линейных уравнений. Основные определения. Матричная запись. 8. Невырожденные системы. Формулы Крамера. Метод Гаусса. 9. Ранг матрицы. Теорема об инвариантности ранга матрицы. 10. Теорема Конекера─Капелли. Решение произвольных систем. 11. Системы однородных линейных уравнений. 12. Понятие вектора. Линейные операции над векторами. 13. Базис и координаты вектора. 14. Прямоугольная система координат. Линейные операции над векторами в линейной форме. 15. Скалярное произведение векторов: его свойства. 16. Векторное произведение векторов: его свойства. 17. Смешанное произведение векторов: его свойства. 18. Необходимое и достаточное условия компланарности векторов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

 (правило Лопиталя).
(правило Лопиталя). следующих функций:
следующих функций: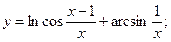
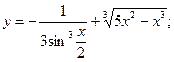
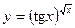


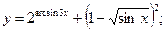

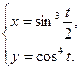
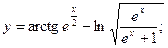

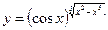
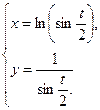
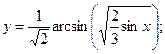
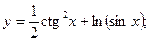
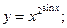

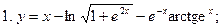
 3.
3. 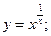
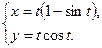

 3.
3.