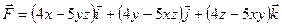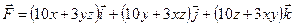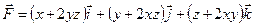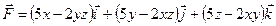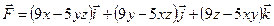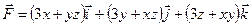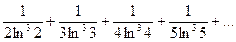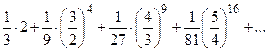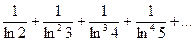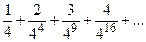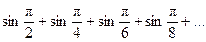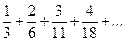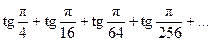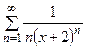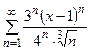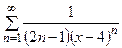Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Аналитическая геометрияСодержание книги
Поиск на нашем сайте
Задания 21─30. Даны координаты вершин пирамиды А1, А2, А3, А4. Найти: 1) площадь грани А1А2А3; 2) объем пирамиды; 3) уравнения прямой А1А2; 4) уравнение плоскости А1А2А3; 5) уравнение высоты А4D, опущенной из вершины А4 на грань А1А2А3; 6) длину высоты А4D; 7) координаты точки пересечения высоты А4D с плоскостью А1А2А3.
21. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0).
22. А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 4).
23. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9).
24. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8).
25. А1 (10; 6; 6), А2 (- 2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3).
26. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9).
27. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3).
28. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7).
29. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7).
30. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
31. Прямые 2 х + у – 1 = 0 и 4 х – у – 11 = 0 являются сторонами треугольника, а точка Р (1; 2) – точкой пересечения третьей стороны с высотой, опущенной на нее. Составить уравнение третьей стороны. Сделать чертеж.
32. Прямая 5 х - 3 у + 4 = 0 является одной из сторон треугольника, а прямые 4 х - 3 у + 2 = 0 и 7 х + 2 у – 13 = 0 его высотами. Составить уравнения двух других сторон треугольника. Сделать чертеж.
33. Точки А (3; -1) и В (4; 0) являются вершинами треугольника, а точка D (2; 1) - точкой пересечения его медиан. Составить уравнение высоты, опущенной из третьей вершины. Сделать чертеж.
34. Прямые 3 х - 4 у + 17 = 0 и 4 х – у – 12 = 0 являются сторонами параллелограмма, а точка Р (2; 7) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж.
35. Прямые х - 2 у + 10 = 0 и 7 х + у - 5 = 0 являются сторонами треугольника, а точка D (1; 3) ─ точкой пересечения его медиан. Составить уравнение третьей стороны. Сделать чертеж.
36. Прямые 5 х - 3 у + 14 = 0 и 5 х - 3 у – 20 = 0 являются сторонами ромба, а прямая х - 4 у – 4 = 0 – его диагональю. Составить уравнения двух других сторон ромба. Сделать чертеж.
37. На прямой 4 х + 3 у – 6 = 0 найти точку, равноудаленную от точек А (1; 2) и В (- 1; - 4). Сделать чертеж.
38. Найти координаты точки, симметричной точке А (5;2) относительно прямой х + 3 у – 1 = 0. Сделать чертеж.
39. Прямые х - 3 у + 6 = 0 и 3 х + у – 12 = 0 являются сторонами прямоугольника, а точка Р (7; 2) – точкой пересечения его диагоналей. Составить уравнения двух других сторон прямоугольника. Сделать чертеж.
40. Точки А (4;5) и С (2; - 1) являются двумя противоположными вершинами ромба, а прямая х – у + 1 = 0 – одной из его сторон. Составить уравнения остальных сторон ромба. Сделать чертеж.
Раздел 3. Введение в математический анализ Задания 41─50. Вычислить пределы.
Раздел 4. Дифференциальное исчисление Функции одной переменной Задания 51─60. Найти производные
52.
53.
54.
55.
56.
57.
58.
59.
60.
Раздел 5. Функции нескольких переменных Задания 61─70. Найти частные производные первого порядка и указанную производную второго порядка от функции:
Задания 71─80. Дана функция 1) градиент функции в точке 2) производную функции в точке
Раздел 6. Неопределенный интеграл Задания 81─90. Найти неопределенные интегралы. В пунктах 1, 2 выполнить проверку дифференцированием. 81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
Раздел 7. Определенный интеграл 91. Вычислить площадь плоской фигуры, ограниченной линиями
92. Вычислить объем тела, полученного вращением вокруг оси oy фигуры, ограниченной линиями 93. Найти длину кривой
94. Вычислить площадь плоской фигуры, ограниченной линиями
95. Вычислить объем тела, полученного вращением вокруг оси ох фигуры, ограниченной линиями у = 0. 96. Найти длину кривой 97. Вычислить площадь плоской фигуры, ограниченной линиями
98. Вычислить объем тела, полученного вращением вокруг оси ох фигуры, ограниченной линиями
99. Найти длину кривой 100. Вычислить площадь плоской фигуры, ограниченной линиями
Раздел 8. Дифференциальные уравнения Задания 101─110. Найти частное решение дифференциального уравнения первого порядка, удовлетворяющее условию 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. Задания 111─120. Найти общее решение дифференциального уравнения.
111. 112. 113. 114. 115. 116. 117. 118. 119. 120.
Раздел 9. Кратные, криволинейные и поверхностные интегралы
Задания 121–130. Изменить порядок интегрирования в двойном интеграле.
121. 122. 123. 124. 125. 126. 127. 128. 129. 130. Задания 131─140. Вычислить объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и его проекции на плоскость
131. 132. 133. 134. 135. 136. 137. 138. 139. 140.
Раздел 10. Элементы теории поля
Задания 141─150. Вычислить работу силы
141. 142.
143.
144.
145.
146. 147.
148.
149.
150.
Задания 151–160. Проверить, является ли векторное поле
151. 152. 153. 154. 155. 156. 157. 158. 159. 160. Раздел 11. Ряды
Задания 161–170. Записать общий член ряда и исследовать ряд на сходимость.
161.
162. 163.
164. 165.
166.
167.
168.
169.
170.
Задания 171–180. Найти область сходимости следующих рядов:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.011 с.) |

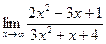


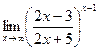

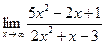

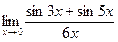
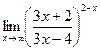


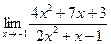
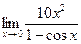


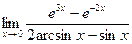








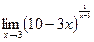
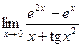




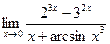
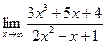



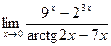
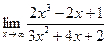
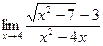


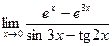




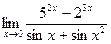
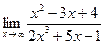
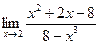
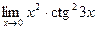
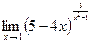
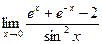
 следующих функций:
следующих функций: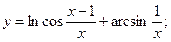
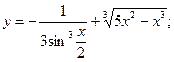
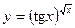


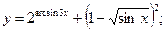

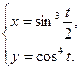
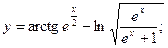

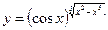
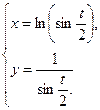
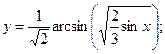
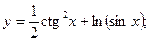
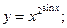

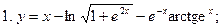
 3.
3. 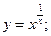
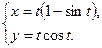

 3.
3. 
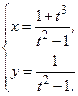







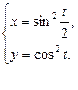

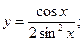
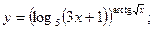
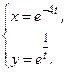
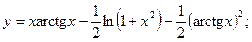

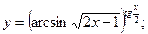
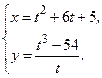


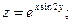


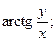
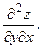

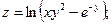
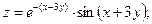

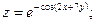
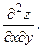
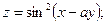
 точка
точка  и вектор
и вектор 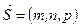 . Найти:
. Найти: ;
; .
.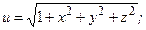

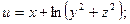


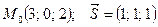




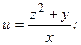


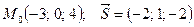



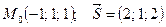
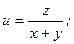
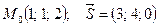



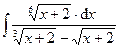


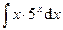
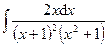
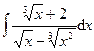
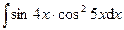
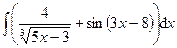
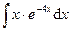
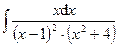

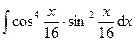

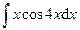



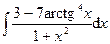
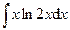

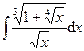

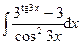



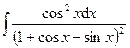
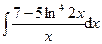


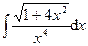


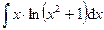

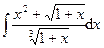




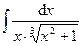
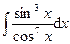

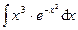
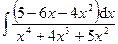
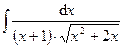
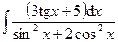
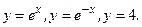
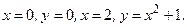
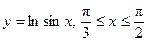 .
.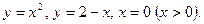
 (одной полуволны),
(одной полуволны),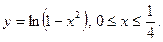
 .
.
 .
.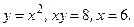
 .
.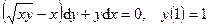

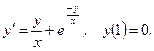
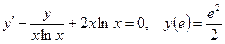

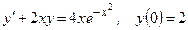
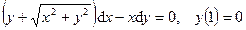


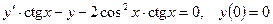




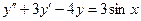

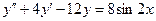
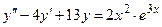


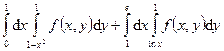


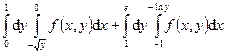


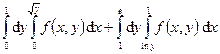

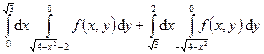

 .
.
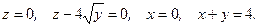
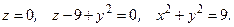
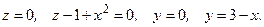
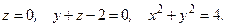
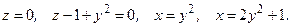
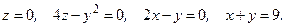


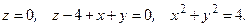
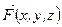 при перемещении материальной точки вдоль линии L от точки А до точки В.
при перемещении материальной точки вдоль линии L от точки А до точки В.
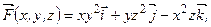
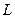 – отрезок прямой,
– отрезок прямой,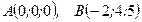
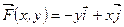 ,
, дуга астроиды
дуга астроиды  ,
, 
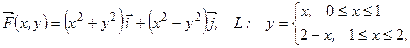
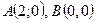
 отрезок прямой,
отрезок прямой,

 L – дуга одного витка винтовой линии
L – дуга одного витка винтовой линии 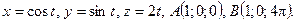
 L – ломаная ACB,
L – ломаная ACB, .
. L – дуга окружности
L – дуга окружности  .
.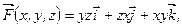 L – дуга винтовой линии
L – дуга винтовой линии  A – точка пересечения линии с плоскостью z = 0, В – точка пересечения линии с плоскостью z = 3.
A – точка пересечения линии с плоскостью z = 0, В – точка пересечения линии с плоскостью z = 3. соленоидальным и потенциальным. В случае потенциальности поля
соленоидальным и потенциальным. В случае потенциальности поля