
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 6. Неопределенный интегралСодержание книги
Поиск на нашем сайте
1. Первообразная. Неопределенный интеграл. 2. Таблица основных интегралов. 3. Основные свойства неопределенного интеграла. 4. Метод замены переменной в неопределенном интеграле. 5. Метод интегрирования по частям. 6. Интегралы от некоторых функций, содержащих квадратный трехчлен. 7. Рациональные дроби. Интегрирование элементарных рациональных дробей. 8. Разложение правильной рациональной дроби на сумму простейших. 9. Интегрирование функций вида 10. Интегрирование тригонометрических функций. 11. Вычисление интегралов вида 12. Интегрирование дифференциальных биномов. 13. Интегралы, не выражающиеся через элементарные функции.
Раздел 7. Определенный интеграл
1. Задачи геометрического и физического содержания, приводящие к понятию определенного интеграла. 2. Определение определенного интеграла. Основные свойства. 3. Теорема об интеграле с переменным верхним пределом. 4. Формула Ньютона─Лейбница. 5. Замена переменной в определенном интеграле. 6. Интегрирование по частям при вычислении определенного интеграла. 7. Вычисление площадей плоских фигур в прямоугольных координатах. 8. Вычисление площадей плоских фигур в полярных координатах. 9. Вычисление длины дуги плоской кривой. 10. Вычисление объема тела по площадям параллельных сечений. 11. Объем тела вращения. 12. Площадь поверхности тела вращения. 13. Правило применения определенного интеграла в конкретных задачах. 14. Интегралы с бесконечными пределами интегрирования. 15. Интегралы от разрывных функций. 16. Признаки сходимости несобственных интегралов.
Раздел 8. Дифференциальные уравнения
1. Обыкновенные дифференциальные уравнения (основные понятия). 2. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши (формулировка). 3. Дифференциальные уравнения с разделяющимися переменными. 4. Дифференциальные уравнения с однородными функциями. 5. Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. 6. Дифференциальные уравнения высших порядков, допускающие понижение порядка. 7. Линейные однородные уравнения n -го порядка; свойства его решений. 8. Теорема о структуре общего решения линейного однородного дифференциального уравнения.
9. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения. 10. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. 11. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида.
Раздел 9. Кратные криволинейные и поверхностные Интегралы 1. Двойной интеграл; его основные свойства. 2. Вычисление двойного интеграла в декартовых координатах. 3. Вычисление двойного интеграла в полярных координатах. 4. Тройной интеграл; его основные свойства. 5. Вычисление тройного интеграла в декартовых координатах. 6. Вычисление тройного интеграла в цилиндрических. 7. Приложение кратных интегралов к решению задач в геометрии. 8. Приложение кратных интегралов к решению задач механики. 9. Криволинейные интегралы первого рода; их свойства и вычисление. 10. Криволинейные интегралы второго рода; их свойства и вычисление. 11. Поверхностные интегралы первого рода; их свойства и вычисление. 12. Поверхностные интегралы второго рода; их свойства и вычисление.
Раздел 10. Элементы теории поля 1. Скалярное поле. Поверхности и линии уровня. 2. Производная по направлению. 3. Градиент скалярного поля; его свойства. 4. Векторное поле. Векторные линии и их дифференциальные уравнения. 5. Поток векторного поля через поверхность. Физический смысл потока в поле скоростей жидкости. 6. Способы вычисления потока векторного поля. 7. Дивергенция векторного поля. 8. Теорема Остроградского─Гаусса. 9. Циркуляция векторного поля. 10. Ротор векторного поля. 11. Теорема Стокса. 12. Соленоидальные поля. 13. Потенциальное поле. Условие потенциальности поля. 14. Гармоническое поле.
Раздел 11. Ряды 1. Числовой ряд. Сумма и остаток ряда. 2. Необходимый признак сходимости ряда. 3. Сравнение рядов с положительными членами. 4. Достаточные признаки сходимости Даламбера и Коши. 5. Интегральный признак Коши. 6. Знакочередующиеся ряды. Признак Лейбница. 7. Знакопеременные ряды. Абсолютная и условная сходимость. 8. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости. 9. Свойства степенных рядов.
10. Ряды Тейлора и Маклорена. 11. Разложение функций sin x, cos x, ex, ln(1 ± x), (1 + x) m в ряды Маклорена. 12. Применение степенных рядов в приближенных вычислениях.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.164.200 (0.009 с.) |

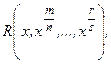
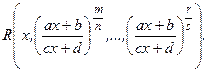
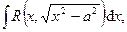
 ,
,  .
.


