
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная зависимость векторов. Базис.Содержание книги
Поиск на нашем сайте
Линейная комбинация – вектор, определяемый по формуле Линейная зависимость – если существуют действительные числа, из которых хотя бы одно отлично от нуля, такие, что Утверждения: Векторы зависимы только тогда, когда по крайней мере один из них является линейной комбинацией остальных. Векторы зависимы только если они коллинеарные. Если a и b – неколлинеарные векторы одной плоскости, то любой третий вектор c той же плоскости можно представить в виде линейной комбинации векторов. Т.е. c = xa + yb. Теорема: Для того чтобы три вектора были линейно независимы, необходимо и достаточно, чтобы они были некомпланарны.
Базис: Три упорядоченных линейно независимых вектора называются базисом в пространстве. Теорема: Любой вектор a в пространстве может быть разложен по базису e1, e2, e3, то есть может быть представлен в виде a = xe1 + ye2 + ze3. (x y z – координаты вектора a в базисе) Базис ортонормированный, если составляющие его векторы перпендикулярны и имеют единичную длину.
15) Линейное преобразование. Собственные числа и собственные векторы линейного преобразования.
Собственные числа и векторы: Ненулевой вектор, удовлетворяющий условию
После нахождения корней уравнения подставляем их в систему, чтобы получить собственный вектор.
Плоскость: уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору; общее уравнение плоскости; исследование общего уравнения плоскости. Уравнение плоскости, проходящей через заданную точку: x1, y1, z1 – координаты точки, лежащей на плоскости. Общее уравнение плоскости: (A, B, C) – координаты вектора нормали. (x1, y1, z1) – координаты точки. Исследования общего уравнения плоскости:
Плоскость: уравнение плоскости, проходящей через три заданные точки; уравнение плоскости «в отрезках».
В координатной форме:
«В отрезках»
Плоскость: угол между плоскостями; взаимное расположение двух плоскостей; нахождение расстояния от точки до плоскости.
Плоскости параллельны, если их векторы нормали коллинеарны. Плоскости перпендикулярны, если их векторы нормали перпендикулярны.
Расстояние от плоскости до точки измеряется длиной перпендикуляра, опущенного из точки на плоскость.
Т.е. чтобы найти расстояние от точки M до плоскости Ax + By + Cz = 0, нужно в левую часть уравнения вместо текущих координат x, y, z, подставить координаты точки M(x1, y1, z1) и разделить полученное число на
Прямая в пространстве: общие уравнения прямой; векторное уравнение прямой; параметрические уравнения прямой; угол между прямыми; взаимное расположение двух прямых.
Векторное уравнение прямой:
Параметрическое уравнение:
Угол между прямыми можно найти с помощью направляющих векторов.
Условия параллельности: Условия перпендикулярности:
Прямая в пространстве: канонические уравнения прямой; уравнение прямой, проходящей через две точки; переход от общих уравнений прямой к каноническим. Каноническое уравнение прямой:
В частном случае, когда направляющий вектор единичный:
Уравнение прямой. Проходящей через две точки.
ð
Переход от общих уравнений к каноническим:
Прямая и плоскость в пространстве: взаимное расположение прямой и плоскости; точка пересечения прямой и плоскости; угол между прямой и плоскостью; пучок плоскостей. Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой и вектор нормали перпендикулярны. Прямая и плоскость перпендикулярны, когда вектор нормали и направляющий вектор параллельны.
Для нахождения точки пересечения прямой и плоскости нужно представить уравнение прямой в параметрическом виде, затем подставить значения x, y, z в уравнение плоскости.
При этом векторы должны быть не перпендикулярны и не параллельны. Для нахождения угла между прямой и плоскостью:
Пучок плоскостей:
Прямая на плоскости: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору; общее уравнение прямой; исследование общего уравнения прямой; взаимное расположение прямых, заданных общими уравнениями. Уравнение: Даны точка Т.к вектор и прямая перпендикулярны, их скалярное произведение равно нулю, т.е, в координатной форме: Общее уравнение прямой - Исследование прямой: При B=0, прямая будет параллельна оси Oy; При C=0, прямая будет проходить через начало координат; При A=C=0, при B не= 0, прямая совпадает с осью Ox; при B=C=0, А не= 0, с осью Oy. Взаимное расположение двух прямых: Параллельны и совпадают, если A/A1 = B/B1 = C/C1, Параллельны и не совпадают, если A/A1 = B/B1 не= C/C1, Пересекаются, если A/A1 не= B/B1.
Прямая на плоскости: векторное уравнение прямой; параметрические уравнения прямой; каноническое уравнение прямой; уравнение прямой, проходящей через две точки; взаимное расположение двух прямых, заданных каноническими уравнениями. r = r0 + st - векторное уравнение прямой. S (m, n) – направляющий вектор, M0(r0)точка на прямой М0(x0, y0).
{х = х0 + mt {y= y0 + nt
x – x0 / m = t и y – y0 / n = t, т.е, x – x0 / m = y – y0 / n = t – каноническое ур-е прямой. Уравнение прямой, через две точки.
Условие параллельности - равное соотношение соответствующих величин. Перпендикулярности – скалярное произведение направляющих векторов = 0.
Прямая на плоскости: уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой с угловым коэффициентом; взаимное расположение двух прямых, заданных уравнениями с угловым коэффициентом; расстояние от точки до прямой. По направлению:
С угловым коэффициентом: Число y = kx + b – уравнение прямой с угловым коэффициентом. b – отрезок, отсекаемы на оси Oy. Прямые:
Расстояние от точки до прямой:
25) Кривые второго порядка. Эллипс: основные определения; вывод канонического уравнения. Эллипс – множество точек плоскости, сумма расстояний до которых до двух данных точек плоскости, называемых фокусами – постоянная величина.
Директрисы:
26) Кривые второго порядка. Гипербола: основные определения; вывод канонического уравнения. Гипербола – множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек этой плоскости, называемых фокусами – постоянная величина.
Директрисы: Ось, сопряженная с гиперболой:
27) Кривые второго порядка. Парабола: основные определения; вывод канонического уравнения. Парабола – множество всех точек плоскости, равноудалённых от точки-фокуса и данной прямой, называемой директрисой.
Директриса:
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.009 с.) |


 . Если таких чисел нет, то векторы линейно независимы.
. Если таких чисел нет, то векторы линейно независимы.

 , называется собственным вектором линейного преобразования A, а соответствующее число – собственное число.
, называется собственным вектором линейного преобразования A, а соответствующее число – собственное число.
 ,
, 
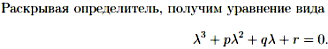
 .
.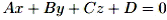 .
.






 , взяв результат по абсолютной величине.
, взяв результат по абсолютной величине.








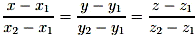 .
.
 ->
-> 



 и вектор
и вектор  ,
, Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
 Параметрическое уравнение:
Параметрическое уравнение:

 называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой.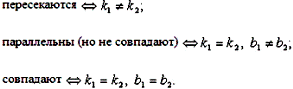
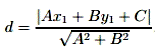


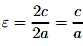 отношение фокального расстояния к длине большой оси (эксцентриситет).
отношение фокального расстояния к длине большой оси (эксцентриситет). (две прямые, перпендикулярные оси Ox, на расстоянии
(две прямые, перпендикулярные оси Ox, на расстоянии  от центра)
от центра)









