
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством) Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.
Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.
Вырожденной матрицей называется такая матрица, определитель которой равен нулю. Теорема: Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством). 1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A. 2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами.
Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли. Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы. Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества. Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая. Теорема Кронекера-Капелли: Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы. При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
Решение систем линейных уравнений: матричный метод, формулы Крамера (с выводом). Матричный метод. Вывод: Матрица-столбец X неизвестных равна произведению обратной матрицы системы на столбец свободных членов. Формулы Крамера. Последовательно заменяются столбцы системы столбцом свободных членов. Определители = значения неизвестных, соответственно заменённым столбцам.
Решение систем линейных уравнений методом Гаусса. Метод – последовательное исключение неизвестных путём элементарных преобразований матрицы.
Однородные системы линейных уравнений, фундаментальная система решений. Однородная система – если свободные члены в системе равны нулю. (=> всегда совместна)
Чтобы система имела ненулевые решения, необходимо и достаточно, чтобы а) ранг её основной матрицы был меньше количества неизвестных, б) определитель = 0. Множество решений, полученных при решении методом Гаусса – фундаментальная система решений.
9) Векторы: Основные определения, линейные операции над векторами, проекция вектора на ось. Вектор – направленный отрезок. Модуль вектора – его длина (| расстояние между его началом и концом |). Нулевой вектор – начало и конец совпадают. Единичный вектор – длина равна единице.
Векторы коллинеарные, если они лежат на одной или на параллельных прямых. Три вектора, если на одной или на параллельных плоскостях. Операции: Сумма векторов – вектор, начало которого совпадает с началом первого, а конец с концом второго, при условии, что второй вектор отложен из конца первого. Разность двух векторов – такой вектор, который при сложении с меньшим равен большему. Произведение вектора на число
Проекция вектора на ось – число, равное произведению длины вектора и угла между осью и этим вектором.
Декартовы прямоугольные координаты вектора в пространстве. Действия над векторами, заданными своими координатами. Деление отрезка в данном отношении. Декартовы прямоугольные координаты вектора – его проекции на координатные оси. Действия над векторами: Сумма векторов – сумма соответствующих координат. Разность – разность соответствующих координат. Произведение вектора на число – произведение координат на число. Деление отрезка в данном отношении:
Прямая на плоскости: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору; общее уравнение прямой; исследование общего уравнения прямой; взаимное расположение прямых, заданных общими уравнениями.
Уравнение: Даны точка Т.к вектор и прямая перпендикулярны, их скалярное произведение равно нулю, т.е, в координатной форме: Общее уравнение прямой - Исследование прямой: При B=0, прямая будет параллельна оси Oy; При C=0, прямая будет проходить через начало координат; При A=C=0, при B не= 0, прямая совпадает с осью Ox; при B=C=0, А не= 0, с осью Oy. Взаимное расположение двух прямых: Параллельны и совпадают, если A/A1 = B/B1 = C/C1, Параллельны и не совпадают, если A/A1 = B/B1 не= C/C1, Пересекаются, если A/A1 не= B/B1.
Прямая на плоскости: векторное уравнение прямой; параметрические уравнения прямой; каноническое уравнение прямой; уравнение прямой, проходящей через две точки; взаимное расположение двух прямых, заданных каноническими уравнениями. r = r0 + st - векторное уравнение прямой. S (m, n) – направляющий вектор, M0(r0)точка на прямой М0(x0, y0).
{х = х0 + mt {y= y0 + nt
x – x0 / m = t и y – y0 / n = t, т.е, x – x0 / m = y – y0 / n = t – каноническое ур-е прямой. Уравнение прямой, через две точки.
Условие параллельности - равное соотношение соответствующих величин. Перпендикулярности – скалярное произведение направляющих векторов = 0.
Прямая на плоскости: уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой с угловым коэффициентом; взаимное расположение двух прямых, заданных уравнениями с угловым коэффициентом; расстояние от точки до прямой. По направлению:
С угловым коэффициентом: Число y = kx + b – уравнение прямой с угловым коэффициентом. b – отрезок, отсекаемы на оси Oy. Прямые:
Расстояние от точки до прямой:
25) Кривые второго порядка. Эллипс: основные определения; вывод канонического уравнения. Эллипс – множество точек плоскости, сумма расстояний до которых до двух данных точек плоскости, называемых фокусами – постоянная величина.
Директрисы:
26) Кривые второго порядка. Гипербола: основные определения; вывод канонического уравнения. Гипербола – множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек этой плоскости, называемых фокусами – постоянная величина.
Директрисы: Ось, сопряженная с гиперболой:
27) Кривые второго порядка. Парабола: основные определения; вывод канонического уравнения. Парабола – множество всех точек плоскости, равноудалённых от точки-фокуса и данной прямой, называемой директрисой.
Директриса:
Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством) Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.
Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.
Вырожденной матрицей называется такая матрица, определитель которой равен нулю. Теорема: Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством). 1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A. 2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами.
Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли. Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы. Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества. Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая. Теорема Кронекера-Капелли: Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы. При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.134.209 (0.01 с.) |





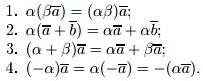


 и вектор
и вектор  ,
, Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
 Параметрическое уравнение:
Параметрическое уравнение:

 называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой.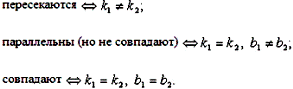
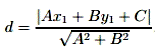


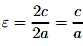 отношение фокального расстояния к длине большой оси (эксцентриситет).
отношение фокального расстояния к длине большой оси (эксцентриситет). (две прямые, перпендикулярные оси Ox, на расстоянии
(две прямые, перпендикулярные оси Ox, на расстоянии  от центра)
от центра)









