
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Обратная матрица. Ранг матрицы.Содержание книги
Поиск на нашем сайте
Обратная матрица Понятие обратной матрицы распространяется только на квадратные матрицы. Определение. Матрица
Теорема. Для того чтобы матрица
Пусть дана невырожденная матрица
тогда обратной к матрице
где Алгоритм нахождения обратной матрицы 1. Найти определитель матрицы 2. Найти алгебраические дополнения всех элементов матрицы
3. Транспонировать матрицу
4. Вычислить обратную матрицу по правилу: 5. Проверить правильность вычисления обратной матрицы, исходя из определения Пример. Найти матрицу обратную к матрице
Решение. 1. Находим определитель матрицы
2. Находим алгебраические дополнения всех элементов данной матрицы:
3. Составляем матрицу
4. Транспонируем матрицу
5. Вычисляем обратную матрицу:
6. Делаем проверку:
Можно показать, что любую невырожденную квадратную матрицу А с помощью отдельных элементарных преобразований только строк или только столбцов можно привести к единичной матрице того же порядка. При этом те же преобразования, совершенные над матрицей Е в том же порядке, приводят ее к обратной матрице
Пример. Найти матрицу обратную к матрице
Решение. 1. Найдем определитель матрицы 2. Приведем матрицу
Поменяем местами первый и второй столбцы, умножим элементы первого столбца на
в результате получим:
3. Умножим элементы второго столбца на 4.
Умножим элементы третьего столбца на
Ранг матрицы Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы. Пусть дана матрица
В матрице А вычеркиванием каких-либо строк или столбцов можно вычленить квадратные подматрицы k -го порядка, где Определение. Рангом матрицы Ранг матрицы обозначается 1. Ранг матрицы 2. 3. Для квадратной матрицы Пример. Вычислить ранг матрицы
Решение. Матрица
Пример. Вычислить ранг матрицы.
Решение. Для матрицы
Поскольку все миноры третьего порядка равны нулю, то ранг матрицы Так как существует ненулевой минор второго порядка, например,
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы. Назовем элементарными преобразованиями матрицы следующие: - отбрасывание нулевой строки (столбца); - умножение всех элементов строки (столбца) матрицы на число не равное нулю; - изменение порядка строк (столбцов) матрицы; - прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; - транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при ее элементарных преобразованиях.
Две матрицы называются эквивалентными, если одна получается из другой с помощью конечного числа элементарных преобразований. Эквивалентные матрицы имеют одинаковые ранги. С помощью эквивалентных преобразований можно привести матрицу к так называемому ступенчатому виду. Матрица
где Замечание. Условие Очевидно, что ранг ступенчатой матрицы равен
Пример. Найти ранг матрицы
Решение. 1. Если
2. Если
3. Если в полученной матрице
Если в процессе преобразования получаются строки (столбцы), целиком состоящие из нулей, то эти строки (столбцы) отбрасываем. Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка не равные нулю, например,
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов. Пусть дана матрица
В матрице
Две строки матрицы называются равными, если равны их соответствующие элементы: Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка
где
Строки матрицы
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Если линейная комбинация строк (2) равна нулю тогда и только тогда, когда все коэффициенты Теорема. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Строки и столбцы матрицы, участвующие в образовании базисного минора, также называются базисными.
Теорема. Всякая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 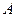 , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:  .
.
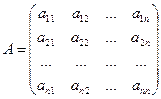 ,
,
 - алгебраические дополнения соответственно элементов
- алгебраические дополнения соответственно элементов  ;
;  .
. :
:

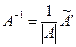

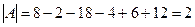
 ,
,  ,
, 
 ,
,  ,
, 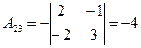
 ,
,  ,
, 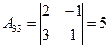




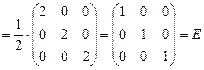

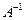 . На этом основан еще один способ нахождения обратной матрицы.
. На этом основан еще один способ нахождения обратной матрицы.
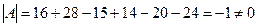 , следовательно, матрица
, следовательно, матрица  одновременно, записывая обе матрицы рядом через черту в виде объединенной матрицы
одновременно, записывая обе матрицы рядом через черту в виде объединенной матрицы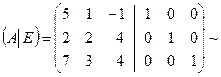
 и прибавим ко второму столбцу, затем умножим элементы первого столбца на
и прибавим ко второму столбцу, затем умножим элементы первого столбца на  и прибавим к третьему столбцу:
и прибавим к третьему столбцу:
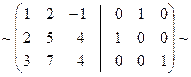
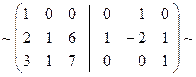
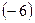 и прибавим к третьему столбцу, в результате получим:
и прибавим к третьему столбцу, в результате получим:

 и прибавим к первому столбцу, а затем ко второму столбцу, в результате получим:
и прибавим к первому столбцу, а затем ко второму столбцу, в результате получим: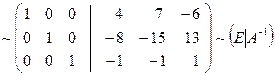 .
. .
.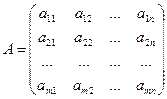
 . Определители таких подматриц называются минорами
. Определители таких подматриц называются минорами  -го порядка матрицы
-го порядка матрицы  можно получить подматрицы первого, второго и третьего порядков.
можно получить подматрицы первого, второго и третьего порядков. или
или  . Из определения следует:
. Из определения следует: не превосходит меньшего из ее размеров, т.е.
не превосходит меньшего из ее размеров, т.е.  .
.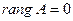 тогда и только тогда, когда все элементы матрицы
тогда и только тогда, когда все элементы матрицы  -го порядка
-го порядка  тогда и только тогда, когда матрица
тогда и только тогда, когда матрица 
 . Однако
. Однако  , т.к. матрица
, т.к. матрица  . Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют определители равные нулю, т.е.
. Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют определители равные нулю, т.е. 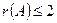 . Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо пропорциональные столбцы (первый и третий), поэтому тоже имеют определители равные нулю. Таким образом,
. Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо пропорциональные столбцы (первый и третий), поэтому тоже имеют определители равные нулю. Таким образом,  . Поскольку матрица
. Поскольку матрица  .
.
 . Проверим, равен ли ранг трем. Для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего четыре, они получаются при вычеркивании одного из столбцов матрицы):
. Проверим, равен ли ранг трем. Для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего четыре, они получаются при вычеркивании одного из столбцов матрицы): ;
;  ;
;  ;
; .
. , то ранг
, то ранг 

 .
.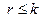 всегда может быть достигнуто транспонированием матрицы.
всегда может быть достигнуто транспонированием матрицы. , так как имеется минор
, так как имеется минор 
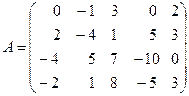
 , то перестановкой строк или столбцов добиваемся того, чтобы
, то перестановкой строк или столбцов добиваемся того, чтобы  . В данном примере поменяем местами первую и вторую строки матрицы.
. В данном примере поменяем местами первую и вторую строки матрицы.
 ) равнялись нулю. В нашем примере умножим первую строку на
) равнялись нулю. В нашем примере умножим первую строку на  и прибавим к третьей строке, затем умножим первую строку на
и прибавим к третьей строке, затем умножим первую строку на  и прибавим к четвертой строке (во второй строке элемент
и прибавим к четвертой строке (во второй строке элемент  , поэтому вторая строка не меняется):
, поэтому вторая строка не меняется):

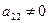 , то умножая элементы второй строки на подходящие числа и прибавляя к третьей и четвертой строкам, добьемся того, чтобы все элементы второго столбца (кроме
, то умножая элементы второй строки на подходящие числа и прибавляя к третьей и четвертой строкам, добьемся того, чтобы все элементы второго столбца (кроме  ) равнялись нулю. В нашем примере умножим вторую строку на
) равнялись нулю. В нашем примере умножим вторую строку на  и прибавим к третьей строке, затем умножим вторую строку на
и прибавим к третьей строке, затем умножим вторую строку на  и прибавим к четвертой строке:
и прибавим к четвертой строке:

 , поэтому ранг полученной ступенчатой, а следовательно и исходной матрицы равен двум
, поэтому ранг полученной ступенчатой, а следовательно и исходной матрицы равен двум  .
. .
.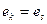 , если
, если  .
. ;
;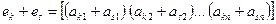 .
. называется линейной комбинацией строк
называется линейной комбинацией строк  матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: ,
, - любые числа.
- любые числа. называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке
, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке (2)
(2) , равны нулю, т.е.
, равны нулю, т.е.  , то строки
, то строки  называются линейно независимыми.
называются линейно независимыми.


