
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства произведения матрицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть 1. 2. 3. 4. 5. Возведение в степень. Целой положительной степенью
Операция возведения в степень определяется только для квадратных матриц. Пример. Найти Решение.
Транспонирование матриц Данная операция состоит в замене строк матрицы на ее столбцы с сохранением их порядка, или, что тоже самое, замене столбцов матрицы на ее строки. Пусть Свойства транспонированных матриц 1. 2. При транспонировании квадратной матрицы элементы, находящиеся на главной диагонали, не меняются. 3. 4. 5.
Для симметрических матриц
Определители квадратных матриц Определителем матрицы первого порядка Определителем матрицы второго порядка или определителем второго порядка называется число, которое вычисляется по формуле
Например, Пусть дана квадратная матрица третьего порядка
Определителем матрицы третьего порядка, соответствующей матрице (1), называется число, обозначаемое символом:
Числа Для вычисления определителя используют правило треугольника: «+» «-»
Пример. Вычислить определитель третьего порядка Решение.
Пусть дана квадратная матрица А n -го порядка. Минором Рассмотрим квадратную матрицу третьего порядка (1). Минором элемента
Минором элемента
Алгебраическим дополнением Пример. Найти алгебраические дополнения всех элементов матрицы
Решение.
Важное значение для вычисления определителей имеет следующая теорема. Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения:
Доказательство. Убедимся в справедливости теоремы на примере определителя третьего порядка. Разложим его по элементам первой строки:
Свойства определителей
1. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю. 2. Умножение всех элементов одного столбца или одной строки определителя на любое число Замечание. За знак определителя можно выносить общий множитель любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех элементов. Пример.
3. Величина определителя не изменится, если его строки и столбцы поменять местами. 4. При транспонировании матрицы ее определитель не изменяется: 5. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный. 6. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю. 7. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю. 8. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю, т.е.
9. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число. 10. Определитель произведения двух квадратных матриц равен произведению их определителей: Замечание. Из свойства 10 следует, что даже если 11. Определитель треугольной матрицы равен произведению ее диагональных элементов. Перечисленные свойства определителей позволяют существенно упростить их вычисления, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1-10, чтобы преобразованная матрица имела строку (столбец), содержащую как можно больше нулей, а затем найти определитель разложением по этой строке (столбцу).
Пример. Вычислить определитель четвертого порядка
Решение. Преобразуем определитель так, чтобы в третьей строке все элементы, кроме одного обращались в нуль. Для этого умножим, например, элементы третьего столбца на (-4) и прибавим их к первому столбцу:
Далее умножим элементы третьего столбца на 2 и прибавим их ко второму столбцу, далее применим к полученному определителю четвертого порядка теорему Лапласа:
Полученный определитель третьего порядка можно вычислить по правилу треугольника или используя теорему Лапласа, но можно продолжить упрощение матрицы. «Обнулим» в матрице третьего порядка элементы второй строки (кроме одного). Для этого умножим элементы третьего столбца на (-13) и на 4 и прибавим соответственно к первому и второму столбцам:
при вычислении определителя второго порядка используем свойство определителя: за знак определителя можно выносить общий множитель любой строки или столбца (вынесем из первого столбца число 8, а из второго столбца число 18):
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

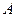 ,
,  и
и  – матрицы, соответствующих размеров (чтобы произведения матриц были определены, а
– матрицы, соответствующих размеров (чтобы произведения матриц были определены, а  - действительное число, тогда:
- действительное число, тогда: .
. .
. .
.
 : произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу.
: произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу. квадратной матрицы
квадратной матрицы 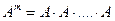
 , где
, где  .
. .
. , тогда транспонированная матрица имеет вид:
, тогда транспонированная матрица имеет вид:  , например
, например  ,
, 
 .
. .
. .
. .
. .
. или определителем первого порядка называется элемент
или определителем первого порядка называется элемент  . Обозначается
. Обозначается  .
. .
. , тогда
, тогда 
 (1)
(1)
 называются элементами определителя. Диагональ, образованная элементами
называются элементами определителя. Диагональ, образованная элементами  , называется главной, а диагональ, образованная элементами
, называется главной, а диагональ, образованная элементами  - побочной.
- побочной.
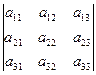
 .
. .
. элемента
элемента  матрицы n -го порядка называется определитель матрицы
матрицы n -го порядка называется определитель матрицы  -го порядка, полученный из матрицы А вычеркиванием i- строки и j- столбца, на пересечении которых расположен этот элемент.
-го порядка, полученный из матрицы А вычеркиванием i- строки и j- столбца, на пересечении которых расположен этот элемент.

 матрицы третьего порядка является определитель второго порядка:
матрицы третьего порядка является определитель второго порядка:

 элемента
элемента  , где
, где 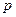 - сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так алгебраическое дополнение элемента
- сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так алгебраическое дополнение элемента  , алгебраическое дополнение элемента
, алгебраическое дополнение элемента 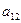 обозначается
обозначается  .
.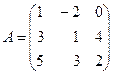
 ;
;  ;
; ;
;  ;
; ;
; 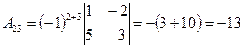 ;
; ;
;  ;
; .
. - разложение по элементам i -ой строки, i=1, 2,…,n.
- разложение по элементам i -ой строки, i=1, 2,…,n. - разложение по элементам j -ого столбца, j=1, 2,…,n.
- разложение по элементам j -ого столбца, j=1, 2,…,n.


 - полученное выражение совпадает с определением определителя третьего порядка. Аналогичный результат получаем при разложении определителя матрицы по любой строке или столбцу.
- полученное выражение совпадает с определением определителя третьего порядка. Аналогичный результат получаем при разложении определителя матрицы по любой строке или столбцу. равносильно умножению определителя на это число.
равносильно умножению определителя на это число. , но
, но
 .
. при
при  .
. ,
,  - матрицы
- матрицы  -го порядка, тогда
-го порядка, тогда  .
. , то
, то  .
.













