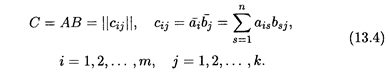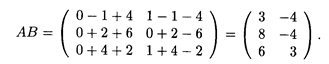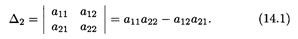Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над матрицамиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1. Сумма матриц. Суммой матриц А и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Представим это в сокращенной записи. Пусть
Тогда сумма этих матриц С = А + В имеет вид
Умножение матрицы на действительное число. Произведением матрицы А на действительное число α называется матрица, каждый элемент которой получен умножением соответствующего элемента матрицы А на число α. Пример 2. Пусть даны матрица А и число α:
Тогда произведением матрицы А на число является матрица
Пусть А, В и С — матрицы, имеющие одинаковый размер, а α и β — некоторые действительные числа. Тогда: 1) А + В = В + А, 2) (А + В) + С = А + (В + С), 3) α(А + В) =αА + αВ, 4) (α + β) A = αA + βA, 5) (αβ)А = (αA)β, 6) A + О = А, где О — нулевая матрица, 7) 0А = О.
55. Умножение матриц. Свойства операции умножения матриц. Умножение матриц — это специфическая операция, составляющая основу алгебры матриц. Строки и столбцы матриц можно рассматривать как векторы-строки и векторы-столбцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов. Пусть даны матрица А размером т х п и матрица В размером п х k. Будем рассматривать матрицу А как совокупность т векторов-строк
Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матрицы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.
Определение 3. Произведением матриц А и В называется матрица С, элементы которой cij равны скалярным произведениям векторов-строк
В операции умножения матриц есть характерная особенность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формирующих элементы соответствующей матрицы, должны участвовать векторы с одинаковым числом координат.
Если матрицы А и В квадратные размером n х n, то имеет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у исходных сомножителей. При этом в общем случае перемножения матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА. Рассмотрим примеры на умножение матриц.
Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:
56. Вырожденные и невырожденные матрицы.
. Матрица порядка п называется вырожденной, если ее ранг r < п.
57. Обратная матрица. Вычисление обратной матрицы методом Жордана-Гаусса Понятие обратной матрицы распространяется только на квадратные матрицы, поэтому здесь и далее мы будем иметь дело с матрицами порядка п. Определение 1. Матрица порядка п называется вырожденной, если ее ранг r < п. Определение 2. Матрица А-1 называется обратной по отношению к матрице А, если их произведение равно единичной матрице:
Несколько забегая вперед, отметим, что для вырожденной матрицы не существует обратной матрицы. Иными словами, если для некоторой матрицы порядка п ее ранг r < п, то для нее не существует обратной матрицы.
58. Запись системы линейных уравнений в матричной форме и ее решение с помощью обратной матрицы. Система т линейных уравнений с п неизвестными (переменными) x 1, x 2,..., xп имеет вид
Здесь aij и bi — произвольные числа (i = 1, 2,..., m; j = 1, 2,..., n), которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений (15.1). Первый индекс у коэффициентов при неизвестных означает номер уравнения, второй индекс соответствует номеру неизвестного xi. Решением системы уравнений (15.1) называется набор п чисел x 1 = α1, x 2 = α2, …, xn = α n, при подстановке которых в эту систему каждое уравнение данной системы превращается в тождество. Система уравнений (15.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.
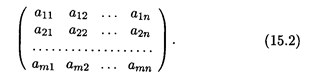
Сведем коэффициенты при неизвестных в системе уравнений (15.1) в матрицу
Эта матрица состоит из m строк и п столбцов и называется матрицей системы. Введем в рассмотрение две матрицы-столбца: матрицу неизвестных Х и матрицу свободных членов В:
Х и В представляют собой векторы-столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее трактовать их именно как матрицы, состоящие соответственно из п и m строк и одного столбца. Тогда систему линейных уравнений (15.1) можно записать в матричной форме, поскольку размер матрицы А равен т х n, а размер Х — n х 1 и, значит, произведение этих матриц имеет смысл:
61. Миноры и алгебраические дополнения. Ранг матрицы. Рассмотрим определитель n -го порядка (14.3). Выделим в нем какой-либо элемент аij и вычеркнем i- ю строку и j- й столбец, на пересечении которых расположен этот элемент. Полученный определитель (n - 1)-го порядка называется минором Mij элемента aij определителя Δ n. Пример 1. Найти минор М 32 определителя четвертого порядка
Решение. Минор М 32 элемента a 32 получается вычеркиванием из данного определителя 3-й строки и 2-го столбца. Полученный определитель 3-го порядка равен
Определение 2. Алгебраическим дополнением элемента aij определителя (14.3) называется число
Так, для приведенного выше примера алгебраическое дополнение равно
1. Пусть дана матрица, содержащая m строк и п столбцов:
Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k -го порядка; определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что в общем случае таких миноров k -го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел т и п, т.е.
Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь среди этих миноров можно найти по крайней мере один минор наибольшего порядка. Определение 1. Наибольший порядок миноров, отличных от нуля, называется рангом матрицы
62. Определитель (детерминант) матрицы. Основная теорема об определителях. Свойства определителей. Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем, или детерминантом, n -го порядка этой матрицы. Начнем с определителей второго и третьего порядков. Пусть дана матрица
тогда ее определитель второго порядка вычисляется по формуле
Определитель третьего порядка вычисляется по формуле
Из данного выше общего определения следуют основные свойства определителей. 1. Если некоторая строка или столбец определителя состоит из нулей, то определитель равен нулю. Действительно, согласно общему определению, в каждое из n! слагаемых обязательно войдет сомножителем элемент нулевой строки (нулевого столбца). 2. При перестановке двух строк (столбцов) определитель меняет знак. Это свойство легко проверяется на определителях второго и третьего порядков. 3. Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.
Действительно, поменяв местами эти строки, получаем Δ n = -Δ n откуда и следует, что Δ n = 0. 4. Общий множитель любой строки (столбца) можно вынести за знак определителя. 5 Если каждый элемент некоторой строки (столбца) определителя Δ n представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, 6. Определитель не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любое число. Это свойство является следствием свойств 3-5. 7. При транспонировании матрицы определитель не меняется.
63. Необходимое и достаточное условия невырожденности матрицы. . Матрица порядка п называется вырожденной, если ее ранг r < п. Квадратная матрица является вырожденной, если ее определитель равен нулю. Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1, определяемую условиями AA -1 = A -1 A = 1. Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является det(A) ≠ 0 или rank(A) = N.
64. Формула для вычисления обратной матрицы. Алгоритм вычисления обратной матрицы. Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение АВ= ВА=Е, где Е – единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Матрица, обратная к А, обозначается через А-1, так что В= А-1. Для матрицы А обратная ей матрица А-1 определяется однозначно. Справедливы следующие равенства: 1) D(А-1)=(DА)-1; 2) (А-1)-1=А; 3) (А1А2)-1=А2-1А1-1; 4) (АТ)-1=(А-1)Т. Существую несколько способов нахождения обратной матрицы. Рассмотрим один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем: пусть нам дана матрица А, имеющая следующий вид:
Предположим, что DА¹0. Построим следующую матрицу С следующим образом:
где Аij – алгебраическое дополнение элемента аij в определителе матрицы А. Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать. Полученная таким образом матрица С называется присоединённой к матрице А, или союзной с А. Чтобы получить матрицу А-1, обратную для матрицы А, необходимо каждый элемент присоединённой матрицы С поделить на DА, т.е. матрица А-1 будет иметь следующий вид:
Пусть матрица А, имеет следующий вид:
Чтобы найти матрицу А-1, обратную для матрицы А, необходимо: - вычислить определитель матрицы (DА= -3); - найти алгебраические дополнения элементов аij в определителе матрицы А:
- составить присоединённую матрицу С по формуле (2); - разделить все элементы матрицы С на DА.
65. Правило Крамера для решения системы п линейных уравнений с п неизвестными. Составим определитель матрицы системы А:
который называется также определителем системы. Заменим в этом определителе j- й столбец на столбец свободных членов В, т.е. получим этой заменой другой определитель, который обозначим Δ j:
Пример 1. Найти решение системы уравнений
Решение. Составим и вычислим определители системы Δ и Δ j (j = x, y, z):
Определитель системы отличен от нуля, стало быть, она имеет единственное решение, которое вычисляется по формулам (15.6):
66. Декартова система координат. Прямая линия. Общее уравнение прямой линии на плоскости. ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене). Общее уравнение прямой линии на плоскости в декартовых координатах:
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A, B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором. При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:
67. Уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках; уравнение прямой, проходящей через две данные (несовпадающие) точки.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.240 (0.013 с.) |


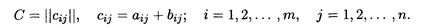


 i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов
i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов  j, каждый из которых содержит по п координат:
j, каждый из которых содержит по п координат: