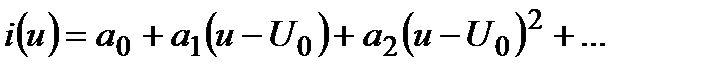Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторный метод анализа линейных стационарных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пребразование Лапласа наряду с перобразованием Фурье широко используется в радиотехнике. Преобразование Лапласа есть функция комплексной переменной
Здесь Важнейшей характеристикой, на которой основан операторный метод, является отношение изображений выходного и входного сигналов:
Эта характеристика называется передаточной функцией или операторным коэффициентом передачи системы. Если эта характеристика известна, то поиск выходной реакции системы на заданное входное воздействие разбивается на три этапа. 1. 2. 3. В общем случае передаточная функция имеет вид
Корни знаменателя Корни числителя Последним этапом решения задачи о прохождении сигнала через линейную стационарную систему с помощью операторного метода является поиск оригинала, которому отвечает изображение формулу обращения
16)Преобразование характеристик случайного процесса в линейных цепях. линейного четырехполюсника с импульсной характеристикой h(t) и частотной передаточной функцией H (j) действует случайный процесс sвх(t) с заданными характеристиками; требуется найти статистические характеристики выходного сигнала sвых(t): распределение вероятностей, корреляционную функцию, спектральную плотность мощности. Самой сложной из этих задач является первая. Она упрощается при нормальном распределении, так как при любых линейных операциях (усилении, фильтрации, дифференцировании, интегрировании) распределение остается нормальным, изменяются лишь функции R(t) и W(), т.е. если задана плотность вероятности флуктуаций случайного процесса в виде
то плотность вероятности выходного сигнала
при этом дисперсия легко определяется по спектру или корреляционной функции.
17) Преобразование сигналов в безынерционных нелинейных цепях нелинейные системы, в которых связь между входным сигналом и выходной реакцией устанавливается нелинейной зависимостью:
Т.о. для исследования нелинейной цепи приходится решать нелинейные дифференциальные уравнения. Для того, чтобы это сделать, необходимо принять, чтобы нелинейная зависимость данного вида (1) не содержала времени. Физически такое требование означает безынерционность нелинейного элемента, т.е. мгновенное установление выходной реакции вслед за изменением внешнего входного воздействия. Безынерционных нелинейных элементов, строго говоря, не существует. Однако эта идеализация достаточно точна, если характерное время изменения входного сигнала значительно превышает время установления процесса внутри самого нелинейного элемента. Это условие безынерционности.
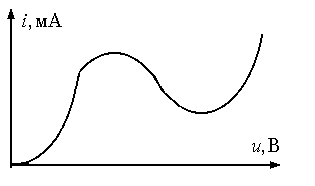
главных характеристик нелинейных элементов является зависимость выходного тока от входного напряжения (Вольт-амперная характеристика). Используемые на практике нелинейные элементы имеют разнообразные характеристики. Можно выделить класс элементов с однозначными ВАХ и класс элементов, характеристики которых содержат участки многозначности.
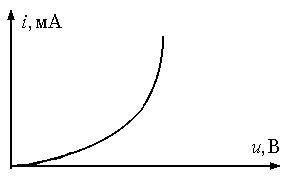
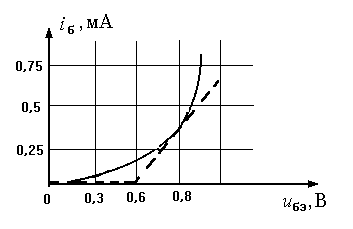
Кусочно-линейную аппроксимацию обычно применяют при расчете процессов в нелинейных элементах в случае больших амплитуд внешних воздействий. Данный способ основан на приближенной замене реальной характеристики отрезками прямых линий с различными наклонами. На рисунке показана входная характеристика реального транзистора, аппроксимированная двумя отрезками прямых.
аппроксимацию широко используют при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия. Этот способ основан на разложении нелинейной вольт-амперной характеристики i(u) в ряд Тейлора, сходящийся в окрестности рабочей точки количество членов разложения зависит от заданной точности.
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 , задаваемая интегралом:
, задаваемая интегралом:
 - комплексная частота. Сигнал
- комплексная частота. Сигнал 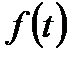 называется оригиналом, а функция
называется оригиналом, а функция 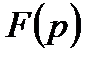 - его изображеним по Лапласу.
- его изображеним по Лапласу.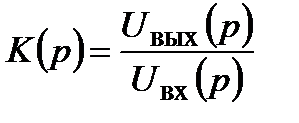
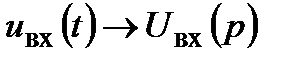


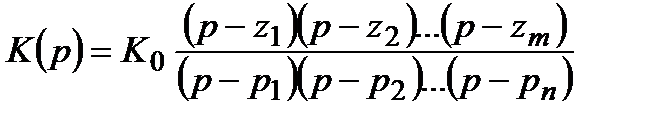
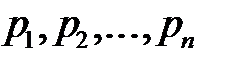 называются полюсами. При равенстве комплексной частоты
называются полюсами. При равенстве комплексной частоты 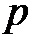 этим корням
этим корням 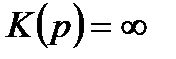 .
. называются нулями. При равенстве комплексной частоты
называются нулями. При равенстве комплексной частоты  .
.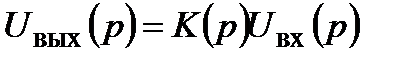 .
.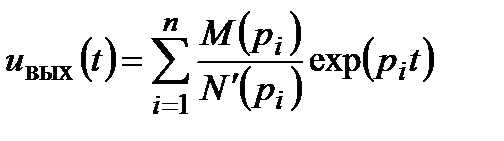 .
.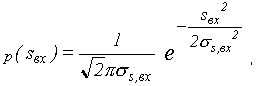
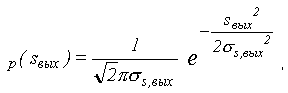
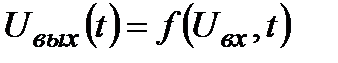 .
.
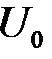 :
: