
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщение теоремы об общем решении на однородные линейные дифференциальные уравнения n-го порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общим решением ЛОДУ n -го порядка
является функция, равная линейной комбинации n линейно независимых частных решений этого уравнения:
Совокупность n линейно независимых частных решений ЛОДУ n -ого порядка называется его фундаментальной системой частных решений (далее – ФСЧР). Линейная независимость функций ФСЧР проверяется через их вронскиан, который должен быть отличен от нуля: Пример 2.Дано ДУ II порядка, линейное, однородное: РЕШЕНИЕ. По теореме об общем решении линейных однородных уравнений II порядка имеем, что где Покажем, что частными решениями данного ДУ являются функции Действительно, Проверяем линейную независимость
Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
где Это уравнение является частным случаем ЛОДУ и известна формула для его общего решения (см. теорему предыдущего параграфа): где Будем искать частные решения Поставив
Таким образом, чтобы функция Уравнение (2) является квадратным уравнением относительно k (в общем случае – алгебраическим уравнением n -ной степени для ЛОДУ n -го порядка). Рассмотрим все возможные случаи для корней характеристического уравнения (2). 1 случай: если это и есть ФСЧР, так как 2 случай: если k 1 = k 2 – действительные равные корни, то имеем только одно частное решение ДУ(1). В этом случае ФСЧР можно взять в виде так как, во-первых, функция во-вторых, функции 3 случай: если Действительно, эти функции являются линейно независимыми, так как Подставим ДУ(1): при этом равенство нулю обозначенных скобок следует из того, что числа Таким образом, показано, что функция Аналогично показывается, что функция По рассмотренным случаям для корней квадратного уравнения (2) можно сформулировать следующее правило, с помощью которого составляется ФСЧР и общее решение ЛОДУ(1).
Примеры Записать общие решения следующих дифференциальных уравнений – линейных, однородных, с постоянными коэффициентами: 1) его характеристическое уравнение: ФСЧР: 2) его характеристическое уравнение: ФСЧР: 3) его характеристическое уравнение: ФСЧР: 4) его характеристическое уравнение: ФСЧР:
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка:
Соответствующее ему линейное однородное ДУ имеет вид
ДОКАЗАТЕЛЬСТВО: Покажем, что функция а) б) содержит нужное количество произвольных постоянных; в) с помощью функции
Действительно, так как Проверим для функции а) подставим б) подставим в и видим, что функция в) решим задачу Коши для дифференциального (1), поставив начальные условия: эти начальные условия подставляем в функцию (3) с учётом равенства (4) для получилась система двух линейных алгебраических уравнений относительно чисел так как поэтому любая задача Коши для ДУ(1) может быть решена. Таким образом, функция ПРИМЕР 1. Решить дифференциальное уравнение второго порядка РЕШЕНИЕ. Так как уравнение является линейным неоднородным, то его общее решение записывается как сумма общего решения соответствующего однородного уравнения и какого-нибудь частного решения неоднородного уравнения: Находим так как уравнение имеет постоянные коэффициенты, то фундаментальную систему его частных решений Универсальным методом для нахождения частного решения линейного неоднородного ДУ является метод вариации произвольных постоянных, который будет рассмотрен далее. В решаемой задаче ограничимся частным решением Тогда записываем общее решение данного уравнения: Доказанная в этом параграфе теорема справедлива для линейных неоднородных уравнений любого порядка, причем, уравнение не обязано иметь постоянные коэффициенты. Однако отработать на практике эту теорему есть возможность только для ЛНДУ с постоянными коэффициентами, так как только в этом случае вполне понятно, как находить общее решение соответствующего ЛОДУ.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.0 (0.009 с.) |



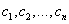 – произвольные постоянные,
– произвольные постоянные,
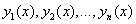 – линейно независимые частные решения ЛОДУ(3').
– линейно независимые частные решения ЛОДУ(3').
 .
.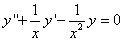 . Найти его общее решение.
. Найти его общее решение.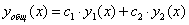 ,
,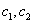 – произвольные постоянные,
– произвольные постоянные, 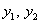 – это ФСЧР.
– это ФСЧР.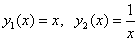 .
. - верно;
- верно;  - верно.
- верно. и
и  :
: 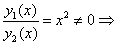 функции
функции 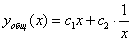 . Для нахождения функций
. Для нахождения функций 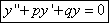 ,
,
 – числа (или const по
– числа (или const по  ).
).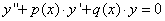 ,
,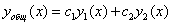 ,
, – произвольные постоянные,
– произвольные постоянные,  – ФСЧР, то есть система двух линейно независимых частных решений.
– ФСЧР, то есть система двух линейно независимых частных решений. .
.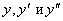 в ЛОДУ(1), получим:
в ЛОДУ(1), получим: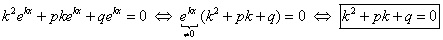
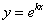 удовлетворяла ЛОДУ(1), нужно, чтобы число k удовлетворяло уравнению (2), которое называется характеристическим уравнениемдля линейного однородного ДУ второго порядка с постоянными коэффициентами.
удовлетворяла ЛОДУ(1), нужно, чтобы число k удовлетворяло уравнению (2), которое называется характеристическим уравнениемдля линейного однородного ДУ второго порядка с постоянными коэффициентами.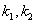 – действительные различные корни, то имеем два частных решения ДУ(1)
– действительные различные корни, то имеем два частных решения ДУ(1) 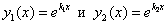 ;
;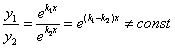 , потому что
, потому что  .
.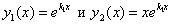 ,
, удовлетворяет ДУ:
удовлетворяет ДУ: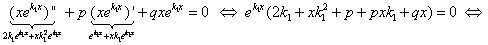
 0=0
0=0 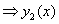 является частным решением;
является частным решением; и
и 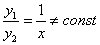 .
.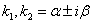 - это комплексно сопряженные корни, то можно показать, что ФСЧР может быть записана в виде
- это комплексно сопряженные корни, то можно показать, что ФСЧР может быть записана в виде  .
.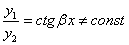 , и каждая из них удовлетворяет ДУ (1), что проверяется их подстановкой в дифференциальное уравнение.
, и каждая из них удовлетворяет ДУ (1), что проверяется их подстановкой в дифференциальное уравнение.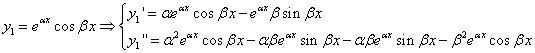
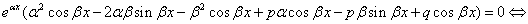
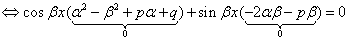 - ДУ удовлетворяется;
- ДУ удовлетворяется; являются корнями характеристического уравнения (2), поэтому
являются корнями характеристического уравнения (2), поэтому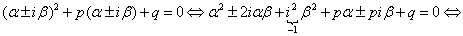
 .
. удовлетворяет ДУ (1), следовательно, является его частным решением.
удовлетворяет ДУ (1), следовательно, является его частным решением. тоже является частным решением ДУ (1) (показать самостоятельно).
тоже является частным решением ДУ (1) (показать самостоятельно). – характеристическое уравнение
– характеристическое уравнение 
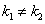 - действительные различные корни,
- действительные различные корни,
 ,
,
 ;
;
 - действительные равные корни,
- действительные равные корни, ,
,
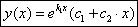 ;
;
 - комплексно сопряженные корни,
- комплексно сопряженные корни,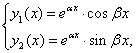 ,
,
 .
.
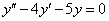 - ЛОДУ II порядка,
- ЛОДУ II порядка,
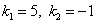 - действительные различные корни
- действительные различные корни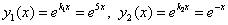
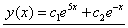 ;
;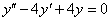 - ЛОДУ II порядка,
- ЛОДУ II порядка,
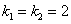 - равные действительные корни
- равные действительные корни
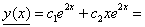
 ;
; - ЛОДУ II порядка,
- ЛОДУ II порядка,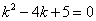

 - комплексно сопряженные корни, в которых
- комплексно сопряженные корни, в которых 

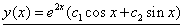 ;
; - ЛОДУ IV порядка,
- ЛОДУ IV порядка,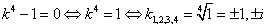 ;
;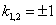 - действительные различные корни
- действительные различные корни 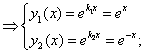
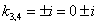 - комплексно сопряженные корни, в которых
- комплексно сопряженные корни, в которых 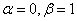 ,
, ;
; ,
, 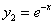 ,
, 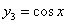 ,
, 

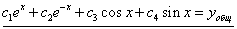 .
.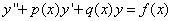 , где
, где  .
.
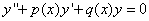
 , или
, или

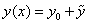 удовлетворяет всем требованиям общего решения ЛНДУ (1), то есть:
удовлетворяет всем требованиям общего решения ЛНДУ (1), то есть: удовлетворяет ДУ;
удовлетворяет ДУ;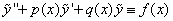 .
.
 – это общее решение ЛОДУ (2), то
– это общее решение ЛОДУ (2), то 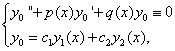 где
где  - это какое-нибудь частное решение неоднородного уравнения, то оно удовлетворяет ЛНДУ (1), то есть
- это какое-нибудь частное решение неоднородного уравнения, то оно удовлетворяет ЛНДУ (1), то есть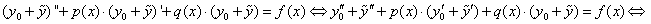

 - ДУ (1) удовлетворяется;
- ДУ (1) удовлетворяется;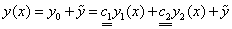
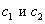 ;
;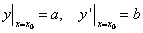 ;
;
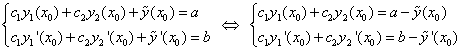
 с главным определителем
с главным определителем 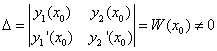 ,
, и
и  – это линейно независимые частные решения однородного ДУ, поэтому их вронскиан
– это линейно независимые частные решения однородного ДУ, поэтому их вронскиан 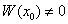 в любой точке
в любой точке  ; по теореме Крамера заключаем, что система уравнений относительно
; по теореме Крамера заключаем, что система уравнений относительно  ,
, .
. , где
, где 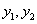 – это ФСЧР;
– это ФСЧР;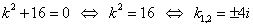 – комплексно сопряженные корни
– комплексно сопряженные корни
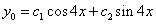 .
. .
. .
.


