
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим ЛНДУ - линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
Его общее решение: Здесь Теперь ставим задачу нахождения Говорят, что правая часть f(x) ДУ (1) имеет специальный вид, если она представлена следующей формулой:
где Ниже приведены примеры различных функций вида (2): Будем рассматривать метод нахождения
ПРИМЕР 1. Найти общее решение ДУ РЕШЕНИЕ. ФСЧР: Находим По правилу 1 записываем вид частного решения Неопределенные коэффициенты А и В находим из условия, что составленное Нахождение 1) при выполнении дифференцирования в этой задаче полезно пользоваться несложным частным алгоритмом: 2) слева от вертикальной черты в указанной схеме проставлены коэффициенты, с которыми 3) подстановка Таким образом, в результате подстановки функции поделив обе части равенства на тождественное равенство многочленов означает совпадение их коэффициентов при одинаковых степенях х, поэтому приравниваем этих коэффициентов получаем систему уравнений для нахождения Найденные коэффициенты А и В подставляем в Проверка ПРИМЕР 2. Найти частное решение ДУ РЕШЕНИЕ. Так как имеем ЛНДУ, то его общее решение имеет форму Находим Находим по правилу 1 записываем вид частного решения неопределенные коэффициенты A, B, C находим из условия, что дифференцирование таким образом, Проверка
Составляем общее решение исходного ДУ: Решаем задачу Коши, удовлетворяя общим решением поставленным начальным условиям: Подставляем вычисленные значения постоянных
Пример 3. Найти частное решение ДУ Решение. Находим α =1 и β = 2 По правилу 2 составляем вид частного решения Неопределенные коэффициенты А и В находим из условия, что составленное Нахождение Используем тождественное равенство тригонометрических выражений: Приравниваем коэффициенты при Итак, получено Проверка: результат подстановки Записываем общее решение неоднородного уравнения: Задача Коши: Подставив найденные значения с1 и с2 в общее решение, получаем частное решение, соответствующее поставленным начальным условиям: Ответ: ЗАМЕЧАНИЯ. 1. В общем случае линейного неоднородного уравнения с постоянными коэффициентами и правой части специального общего вида (2) частное решение ищется в следующем виде: Здесь r – это кратность чисел (α±iβ) как корней характеристического уравнения (r = 0 – не являются корнями, r=1 – простые корни, r=2 – двукратные корни и т.д.). 2. Принцип суперпозиции (наложения) частных решений ЛНДУ позволяет расширить возможности работы по сформулированным правилам 1 и 2. ПРИМЕР 4. Найти общее решение ЛНДУ РЕШЕНИЕ. Находим где По принципу наложения частных решений составляем Находим по правилу 2 составляем и находим коэффициенты А и В: таким образом, проверка ДУ: Находим по правилу 1 составляем ДУ: Ответ:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 3249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.209 (0.007 с.) |

 .
.
 -- по теореме об общем решении ЛНДУ.
-- по теореме об общем решении ЛНДУ. – это общее решение соответствующего однородного уравнения с постоянными коэффициентами, которое находится по корням характеристического уравнения:
– это общее решение соответствующего однородного уравнения с постоянными коэффициентами, которое находится по корням характеристического уравнения:
 – корни характеристического уравнения.
– корни характеристического уравнения. – какого-нибудь частного решения ЛНДУ(1).
– какого-нибудь частного решения ЛНДУ(1). ,
,
 ,
, 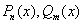 - целые многочлены степени
- целые многочлены степени  и
и 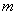 .
.
 - первый специальный вид, то
- первый специальный вид, то

 и
и  ;
- в случае
;
- в случае  и
и  .
.
 – это многочлен той же степени n, что и
– это многочлен той же степени n, что и 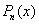 , взятый в самом общем виде с неопределенными коэффициентами:
, взятый в самом общем виде с неопределенными коэффициентами: 
 - линейного, неоднородного, с постоянными коэффициентами.
- линейного, неоднородного, с постоянными коэффициентами.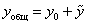 . Находим
. Находим  характеристическое уравнение
характеристическое уравнение 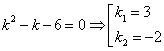 - действительные различные корни
- действительные различные корни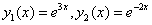

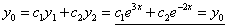 .
. -- подходит под первый специальный вид, причем
-- подходит под первый специальный вид, причем  совпадает с одним из корней характеристического уравнения.
совпадает с одним из корней характеристического уравнения. .
. Пояснения к схеме:
Пояснения к схеме: ;
; и
и 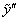 входят в исходное ЛНДУ;
входят в исходное ЛНДУ;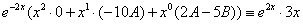 ;
; , получаем тождественное равенство двух многочленов первой степени:
, получаем тождественное равенство двух многочленов первой степени: ;
; и
и  :
:
 .
. результат подстановки
результат подстановки  , следовательно,
, следовательно,  и получаем общее решение данного в задаче ЛНДУ. Ответ:
и получаем общее решение данного в задаче ЛНДУ. Ответ:  .
. .
. .
. , где
, где  ,
,  - это ФСЧР,
- это ФСЧР,  ,
, 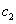 - произвольные постоянные; так как ЛОДУ имеет постоянные коэффициенты, то ФСЧР можно найти с помощью характеристического уравнения:
- произвольные постоянные; так как ЛОДУ имеет постоянные коэффициенты, то ФСЧР можно найти с помощью характеристического уравнения: - равные действительные корни
- равные действительные корни .
.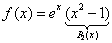 - подходит под первый специальный вид, в котором
- подходит под первый специальный вид, в котором 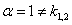 ;
;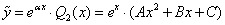 ;
;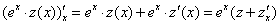 :
: далее разделим обе части равенства на
далее разделим обе части равенства на  и получим тождественное равенство двух многочленов, которое означает совпадение их коэффициентов при одинаковых степенях
и получим тождественное равенство двух многочленов, которое означает совпадение их коэффициентов при одинаковых степенях  :
: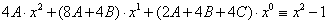

 ;
;
 ;
;
 ;
; .
.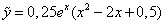


 – верно.
– верно. .
. ;
;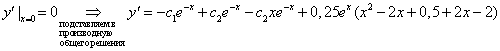

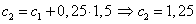 .
. . Для ответа выполняем группировку слагаемых и упрощение коэффициентов. Ответ:
. Для ответа выполняем группировку слагаемых и упрощение коэффициентов. Ответ: 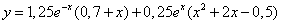 .
.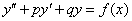 имеет следующий вид:
имеет следующий вид:
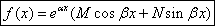 – второй специальный вид,
то
– второй специальный вид,
то  Неопределенные коэффициенты А, В находятся из условия, что
Неопределенные коэффициенты А, В находятся из условия, что  ,
,  ,
,  .
.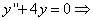 характеристическое уравнение
характеристическое уравнение  - комплексно-сопряженные
- комплексно-сопряженные 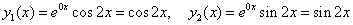
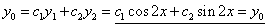 .
. – подходит под второй специальный вид, в котором
– подходит под второй специальный вид, в котором .
. .
.
 .
.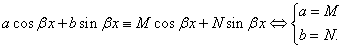
 и
и  и вычисляем коэффициенты А и В:
и вычисляем коэффициенты А и В:
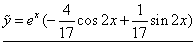 .
.
 .
. .
. ;
; .
.
 .
. .
. – большая из степеней многочленов
– большая из степеней многочленов  ;
; -- целые многочлены степени k, взятые в самом общем виде с неопределенными коэффициентами;
-- целые многочлены степени k, взятые в самом общем виде с неопределенными коэффициентами;
 .
. ,
, – подходит под второй специальный вид,
– подходит под второй специальный вид, – подходит под первый специальный вид.
– подходит под первый специальный вид. , где
, где  удовлетворяет ДУ
удовлетворяет ДУ  ,
,  удовлетворяет ДУ
удовлетворяет ДУ  .
. - второй специальный вид, в котором
- второй специальный вид, в котором 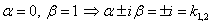 ;
;
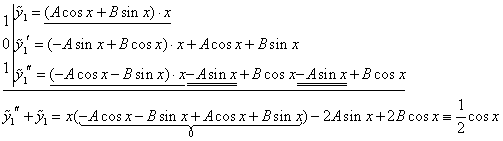

 ;
;
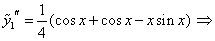
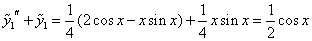 – верно.
– верно.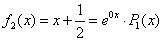 – первый специальный вид, в котором
– первый специальный вид, в котором  ;
; и находим коэффициенты
и находим коэффициенты 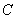 и
и  :
: ;
; .
. .
.


