
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая трактовка основных понятий ДУ I порядкаСодержание книги
Поиск на нашем сайте
Общее решение: ЧАСТНОЕ РЕШЕНИЕ: Начальное условие: Дифференциальное уравнение ПРИМЕР 3. Решаем задачу Коши, то есть ищем интегральную линию, проходящую через точку Геометрический смысл ДУ: Важное значение в теории ДУ имеет теорема существования и единственности частных решений, или решения задачи Коши (без доказательства, рассматриваем только для ДУ I порядка).
То есть если условия теоремы выполнены, то существует единственная интегральная линия данного ДУ, проходящая через точку Если же условия теоремы не выполнены, то нельзя гарантировать существование и единственность интегральной линии, проходящей через точку не существует интегральной линии, проходящей через точку существует интегральная линия, проходящая через точку
существует единственная интегральная линия, проходящая через точку Точки Пример 4 1) Поэтому в любой точке
По теореме существования и единственности заключаем, что 1) через любую точку (x, y), в которой x ≠ 0, проходит единственная интегральная линия; 2) через любую точку (0, y) нельзя гарантировать прохождение единственной интегральной линии.
Все точки ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА (РЕШЕНИЕ ДУ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ, ОДНОРОДНЫЕ ДУ, ЛИНЕЙНЫЕ ДУ, ДУ БЕРНУЛЛИ) Основные типы ДУ I порядка, их каноническая форма и суть методов решения 1. ДУ с разделяющимися переменными: нужно разделить переменные и проинтегрировать обе части равенства с добавлением константы. 2. Однородные ДУ: нужно заменить 3. Линейные ДУ I порядка: нужно заменить 4. ДУ Бернулли, или обобщенное линейное: нужно заменить Если общее решение ДУ выражается через интегралы, то говорят, что дифференциальное уравнение интегрируемо в квадратурах. Например, 1)
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.6.24 (0.008 с.) |

 – это однопараметрическое (параметр –
– это однопараметрическое (параметр – 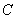 ) семейство линий на координатной плоскости
) семейство линий на координатной плоскости  , которые называются интегральными линиями дифференциального уравнения.
, которые называются интегральными линиями дифференциального уравнения. – это одна из интегральных линий.
– это одна из интегральных линий. - фиксирует точку
- фиксирует точку  , через которую проходит интегральная линия, соответствующая частному решению, полученному по этому начальному условию.
, через которую проходит интегральная линия, соответствующая частному решению, полученному по этому начальному условию. – задает в каждой точке
– задает в каждой точке  значение производной
значение производной 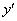 , что геометрически равно значению углового коэффициента касательной к интегральной линии. Следовательно, ДУ задает поле направлений касательных к интегральным линиям.
, что геометрически равно значению углового коэффициента касательной к интегральной линии. Следовательно, ДУ задает поле направлений касательных к интегральным линиям.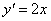 - ДУ I порядка.
- ДУ I порядка.  Его общее РЕШЕНИЕ:
Его общее РЕШЕНИЕ: 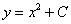 – это однопараметрическое семейство интегральных линий, имеющих форму парабол с вершинами по оси OY. Начальное условие:
– это однопараметрическое семейство интегральных линий, имеющих форму парабол с вершинами по оси OY. Начальное условие: 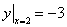 - фиксирует на плоскости XOY точку
- фиксирует на плоскости XOY точку  .
. - это значение постоянной
- это значение постоянной  – искомое частное решение, график которого проходит через точку
– искомое частное решение, график которого проходит через точку  к интегральной линии в каждой точке
к интегральной линии в каждой точке  .
. , стоящая в правой части дифференциального уравнения, в точке
, стоящая в правой части дифференциального уравнения, в точке  , то ДУ имеет единственное частное решение, удовлетворяющее поставленному начальному условию.
, то ДУ имеет единственное частное решение, удовлетворяющее поставленному начальному условию.
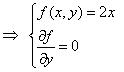 обе функции непрерывны при любых
обе функции непрерывны при любых  -
-
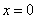 .
.
 Общее решение данного ДУ:
Общее решение данного ДУ: 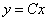 - это семейство прямых, проходящих через начало координат.
- это семейство прямых, проходящих через начало координат. являются особыми точками этого ДУ. Через одну из них
являются особыми точками этого ДУ. Через одну из них  проходят все интегральные линии; через остальные особые точки (точки оси OY) не проходит ни одна из интегральных линий данного ДУ.
проходят все интегральные линии; через остальные особые точки (точки оси OY) не проходит ни одна из интегральных линий данного ДУ.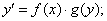




 , где
, где 

 данное ДУ интегрируемо в квадратурах;
данное ДУ интегрируемо в квадратурах;



