
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Будем рассматривать следующие три типа ДУ, допускающих понижение порядка.Содержание книги
Поиск на нашем сайте
Решаются 2. Дифференциальные уравнения, не содержащие явно искомую функцию
Метод решения: замена ДУ (5) 3. Дифференциальные уравнения, не содержащие явно независимую переменную
Метод решения: замена тогда ДУ(6) ПРИМЕР 1. Найти частное решение ДУ РЕШЕНИЕ. Данное уравнение является простейшим ДУ третьего порядка, решаем его трехкратным интегрированием: 1) так как по определению третьей производной имеем, что найдем 2) теперь в 3) подставив ПРИМЕР 2. Найти общее решение дифференциального уравнения РЕШЕНИЕ. Данное ДУ второго порядка не содержит в явном виде искомую функцию Исходное ДУ ДУ относительно ДУ относительно Общее решение ДУ I порядка: Возвращаемся к искомой функции Проверка: Решение любого ДУ можно подтвердить проверкой. Сделаем это в решаемой задаче. подставляем следовательно, общее решение найдено правильно. Ответ: ПРИМЕР 3 Найти общее решение дифференциального уравнения РЕШЕНИЕ. Данное ДУ II порядка не содержит независимую переменную Здесь при пересчете второй производной использовано правило дифференцирования сложной функции: Исходное ДУ его решение: а) б) Возвращаемся к функции Объединяем обе части общего решения:
4.1 Общие определения Линейным дифференциальным уравнением Общий вид линейного ДУ n-го порядка относительно функции
Линейное ДУ(1) называется линейным однородным дифференциальным уравнением (ЛОДУ), если его правая часть равна нулю, то есть функция Общий вид линейного однородного ДУ n-го порядка:
Линейное ДУ(1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ), если его правая часть есть отличная от нуля функция, то есть Говорят, что линейное однородное дифференциальное уравнение (2) сопутствует, или сопровождает, или соответствует линейному неоднородному дифференциальному уравнению (1). Если в ДУ(1) все коэффициенты Общность не нарушается, если изучение линейных ДУ и методов их решения рассмотреть на примере линейных ДУ II порядка: Каноническая форма линейных ДУ второго порядка:
В частности, для ДУ(1') с постоянными коэффициентами функции Основные свойства решений линейных однородных ДУ Будем рассматривать ЛОДУ второго порядка
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.203 (0.007 с.) |


 - кратным интегрированием.
- кратным интегрированием.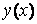 :
: .
.
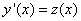

 ;
; – получилось ДУ I порядка относительно функции
– получилось ДУ I порядка относительно функции  .
. :
:

 , то есть
, то есть  ;
;
 - получилось ДУ I порядка, в котором
- получилось ДУ I порядка, в котором  – это независимая переменная,
– это независимая переменная,  – искомая функция.
– искомая функция. ,
,  ,
,  .
.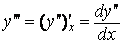 , то
, то
 ;
; из условия
из условия  :
:  ;
; подставим
подставим  и используем определение второй производной:
и используем определение второй производной: 

 ; найдем
; найдем  из условия
из условия  :
:  ;
;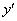 , заменим
, заменим  :
: 
 ; найдем
; найдем  из условия
из условия 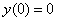 :
: 
 .Получили решение задачи Коши, причем, без нахождения общего решения:
.Получили решение задачи Коши, причем, без нахождения общего решения:  . Ответ:
. Ответ:  .
. .
. , поэтому допускает понижение порядка, как ДУ вида (5). Заменим:
, поэтому допускает понижение порядка, как ДУ вида (5). Заменим:  .
.
 - это линейное ДУ I порядка относительно функции
- это линейное ДУ I порядка относительно функции 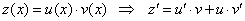 , тогда
, тогда 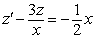
 .
. :
: 
 .
. :
:  .
. .
.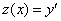 , то получили, что
, то получили, что  это дифференциальное уравнение I порядка относительно функции
это дифференциальное уравнение I порядка относительно функции 
 – это общее решение исходного ДУ.
– это общее решение исходного ДУ.
 в исходное ДУ:
в исходное ДУ: - верно,
- верно,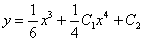 .
. .
. .
. .
.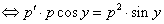 – получили ДУ I порядка относительно функции
– получили ДУ I порядка относительно функции 
 – это первая часть общего решения исходного ДУ;
– это первая часть общего решения исходного ДУ;


 .
. :
:  – это ДУ I порядка относительно функции
– это ДУ I порядка относительно функции 
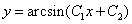 - это вторая часть общего решения исходного ДУ.
- это вторая часть общего решения исходного ДУ.
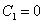 ; поэтому вторая часть включает в себя первую, то есть является их объединением. Ответ:
; поэтому вторая часть включает в себя первую, то есть является их объединением. Ответ: 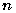 -го порядка называется ДУ, в которое неизвестная функция и все её производные входят линейно, то есть только в первых степенях и не перемножаются.
-го порядка называется ДУ, в которое неизвестная функция и все её производные входят линейно, то есть только в первых степенях и не перемножаются. :
:
 - коэффициенты линейного ДУ (непрерывные функции от x),
- коэффициенты линейного ДУ (непрерывные функции от x),  ;
;
 - правая часть линейного ДУ;
- правая часть линейного ДУ;
 - коэффициент при старшей производной отличен от нуля.
- коэффициент при старшей производной отличен от нуля.
 .
.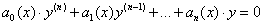
 .
.
 и
и  будут постоянными числами.
будут постоянными числами.



