
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные корректирующие кодыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Надежность передачи сообщений по каналу связи при наличии помех зави-сит от вида выбранного кода. Под кодом будем понимать множество разрешенных (передаваемых) кодовых слов, которые выбираются из множества входных канальных последовательностей (кодовых слов). Разрешенные кодовые слова (код) следует выбрать таким образом, чтобы вероятность ошибки была мини-мальной. Вероятность ошибки в данном случае является критерием, т.е. коли-чественной характеристикой качества функционирования системы связи. Она показывает как часто ошибается приемник(код) в заданной помеховой обстано-вке и позволяет выбрать наилучший. Приемник (код), обеспечивающий мини-мум вероятности ошибки, называется оптимальным в заданной помеховой обс-тановке. Этот критерий был предложен академиком Котельниковым, а соответ-ствующий оптимальный приемник был назван им «идеальным наблюдателем». С целью уменьшения вероятности ошибки, разрешенные кодовые слова следует выбирать так, чтобы они как можно меньше были похожи друг на друга, что повышает надежность их различения на фоне помех. В качестве меры различия кодовых слов выбирается расстояние Хемминга, т.е. количество разрядов, в которых кодовые слова различаются. Поэтому корректирующую способность кода можно характеризовать минимальным расстоянием d между разрешенными кодовыми словами, которое называется минимальным кодовым расстоянием. Декодирование осуществляется по минимуму расстояния Хемминга между принятым кодовым словом и разрешенными кодовыми словами, которые хранятся в памяти приёмника, т.е. решение принимается в пользу разрешенного кодового слова, наиближайшего к принятому. В этом случае ошибки кратности t ≤ d – 1 обнаружимы, а кратности t < При большой длине кодовых слов такой способ декодирования не удается реализовать в реальном масштабе времени из-за большого объема вычислений и, кроме этого, требуется большой объем памяти для хранения кодовых слов. Преодолеть указанные трудности, в частности, позволяет использование линейных корректирующих кодов. В этом случае вместо запоминания всех разрешенных кодовых слов запоминается только система линейных уравнений, решениями которой являются разрешенные кодовые слова. Основной задачей построения линейных корректирующих кодов является выбор системы линейных уравнений, которая записывается в виде:
…………………………….
или в матричном виде H В случае линейных корректирующих кодов сумма двух разрешенных кодовых слов является разрешенным кодовым словом. Это основное свойство, которое можно использовать в качестве определения линейного корректирую-щего кода, следует из равенства
где Рассмотрим декодирование по синдрому, использующее согласно выбранной модели канала связи принятое кодовое слово Если Поскольку система уравнений линейна (Н – линейный оператор), то спра-ведливы следующие преобразования:
отсюда Равенство Каждому значению синдрома, количество которых равно 2m, априори до приема кодового слова Решение принимается в пользу кодового слова Таким образом, при декодировании по принятому вектору Декодирование по минимуму расстояния, по синдрому и по максимуму апостериорной вероятности Эквивалентность декодирования по минимуму расстояния и по синдрому следует из равенства Вектор Рассмотрим некоторые свойства линейных кодов. Количество векторов
Отсюда следует, что сумма Таким образом, если один из векторов подмножества выбрать в качестве исходного (порождающего), то все остальные можно получить в результате его сложения последовательно с каждым разрешенным кодовым словом, количест-во которых равно 2k. Минимальное кодовое расстояние в случае линейных кодов совпадает с минимальным весом разрешенных кодовых слов. Действительно, расстояние между двумя кодовыми словами измеряется весом их суммы. Для линейного кода эта сумма совпадает с одним из разрешен-ных кодовых слов, вес которого определяет расстояние между двумя выбран-ными разрешенными кодовыми словами.
Декодирование по синдрому:
Рассмотрим декодирование по синдрому, использующее согласно выбранной модели канала связи принятое кодовое слово Если Поскольку система уравнений линейна (Н – линейный оператор), то спра-ведливы следующие преобразования:
отсюда Равенство Каждому значению синдрома, количество которых равно 2m, априори до приема кодового слова Решение принимается в пользу кодового слова Таким образом, при декодировании по принятому вектору Декодирование по минимуму расстояния, по синдрому и по максимуму апостериорной вероятности Эквивалентность декодирования по минимуму расстояния и по синдрому следует из равенства Вектор Рассмотрим некоторые свойства линейных кодов. Количество векторов
Отсюда следует, что сумма Таким образом, если один из векторов подмножества выбрать в качестве исходного (порождающего), то все остальные можно получить в результате его сложения последовательно с каждым разрешенным кодовым словом, количест-во которых равно 2k. Минимальное кодовое расстояние в случае линейных кодов совпадает с минимальным весом разрешенных кодовых слов. Действительно, расстояние между двумя кодовыми словами измеряется весом их суммы. Для линейного кода эта сумма совпадает с одним из разрешен-ных кодовых слов, вес которого определяет расстояние между двумя выбран-ными разрешенными кодовыми словами. Рассмотрим свойства матрицы H, которые гарантируют заданное значение минимального кодового расстояния. Для каждого кодового слова уравнение …… означает, что сумма некоторого подмножества столбцов матрицы….. равна 0. Приумножении матрицы …… на вектор-столбец …… из матрицы выбираются столбцы, которым соответствуют единицы в векторе ….. Поскольку минимальное кодовое расстояние равно минимальному весу кодовых слов, то должно существовать, по крайней мере, одно подмножество, состоящее из d столбцов матрицы H, сумма которых равна 0. С другой стороны, не может существовать ни одного подмножества из d-1 или менее столбцов, сумма которых равна 0. Если рассматривать столбцы матрицы … как векторы, то можно сказать, что для кода с кодовым расстоянием, равным …, все подмножества из ….. столбцов должны быть линейно независимыми. Это утверждение составляет одну из фундаментальных теорем о групповых кодах. Оно позволяет находить кодовое расстояние … группового кода, заданного матрицей …, а также строить матрицы..,гарантирующие заданное минимальное кодовое расстояние. Декодированию по синдрому можно дать следующую физическую интер-претацию: вектор По синдрому с некоторой точностью восстанавливается (оценивается) вид вектора ошибок на входе фильтра. Оценка
При декодировании ошибка отсутствует, когда
Доп. Инфа:
Свойства энтропии Энтропия При равномерном распределении (pi= Докажем, что это максимальное значение энтропии. Используя равенство Н(Х)-logmX= Для оценки выражения log
Заменяя
где log e —модуль перехода. Отсюда
Пусть множество состоит из двух элементов, которые обозначим через единицу и ноль, причем единица появляется с вероятностью, равной р, а ноль — с вероятностью, равной q=1 — р. Тогда
Указанная зависимость изображена на рис. 1. Максимум достигается при p=q= 0,5. Билет 6.
а)Энтропия и её свойства. Энтропия которое необходимо для определения состояния одного разряда. Величина Из лабораторной 1: Предельные возможности определяются энтропией. Если она Энтропия: p- вер-ть появления еденицы в массиве Энтропия это количество информации которое приходится на один разряд. Из лабораторной 2: Проблема передачи непрер. сообщ-я закл. в получ. его копии на приемном пункте. Не сущ-ет способа, позвол-го получить точную копию перед-ого сообщ-я, поск. это требует бесконечной точности его воспроизв-я. Поэт. задают точность воспр-я перед-ого сообщ-я. воспр-я перед-ого сообщ-я. энтропия – это min кол-во инфы, кот. необх. передать по каналу, чт. восст. сообщение с заданной точностью Свойства энтропии Энтропия При равномерном распределении (pi= Докажем, что это максимальное значение энтропии. Используя равенство Н(Х)-logmX= Для оценки выражения log
Заменяя
где log e —модуль перехода. Отсюда
Пусть множество состоит из двух элементов, которые обозначим через единицу и ноль, причем единица появляется с вероятностью, равной р, а ноль — с вероятностью, равной q=1 — р. Тогда
Указанная зависимость изображена на рис. 1. Максимум достигается при p=q= 0,5.
б)Дискритизация непрерывных сообщений. Теорема Котельникова. Пространство сигналов. Произвольную кусочно-непрерывную функцию
если энергия функции Бесконечная система действительных функций
а отдельная функция
При заданной системе функций
достигает минимума. Минимум среднеквадратичной ошибки достигается в том случае, когда коэффициенты ряда определяются по формуле
Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье. Ортогональная система называется полной, если путем увеличения количества членов в ряде среднеквадратичную ошибку можно сделать сколь угодно малой. Таким образом, по счетному множеству коэффициентов
Последнее равенство является обобщением теоремы Пифагора на случай n -мерного пространства. Путем непосредственных вычислений легко установить, что энергия сигнала
Таким образом, дискретизацией называется замена непрерывной функции Выбор системы ортогональных функций С целью передачи сигнала по каналу связи широко применяется разложение функции Согласно теореме Котельникова произвольная функция
образующие систему ортогональных функций, отличаются друг от друга только сдвигом по оси времени t на величину кратную
которую в результате тождественных преобразований можно привести к виду: Если дискретизации подлежит нормальный (гауссов) случайный процесс, энергетический спектр которого имеет прямоугольную форму, то коэффициенты Таким образом, непрерывные сообщения можно передавать в цифровом виде, то есть в виде последовательности чисел, при этом каждое число приближенно выражает величину соответствующего коэффициента
Билет 7. 1.Взаимная информация и её свойства. Источник информации и приемник можно рассматривать как подсистемы одной сложной системы. Взаимную информацию между состояниями подсистем, можно записать в виде
Поскольку сложная система случайным образом приходит в то или иное состояние, определяемое парой чисел (xi,yj), то I (xi,yj) будет случайной величиной, которую можно усреднить по всему множеству состояний. В результате почленного усреднения (4) получим выражение для средней (полной) взаимной информации:
где I(y,x)=
С точки зрения информационного описания системы связи безразлично, какую из подсистем рассматривать в качестве передатчика, а какую в качестве приемника. Поэтому энтропии Н (Х) и H (У) можно интерпретировать как информацию, которая поступает в канал связи, а условные энтропии H (X | Y), H (Y | X) как информацию, которая рассеивается в канале. В [1] доказано, что 1(Х, У)≥0. При выполнении указанного неравенства из (5) следует, что
Условную энтропию можно представить в виде
где величина
Таблица 1
При наличии статистической зависимости энтропия H (X | yj) может оказаться как меньше, так и больше Н (Х). Напомним, что для энтропии H (X | Y) всегда справедливо неравенство H (X | Y)≤ H (X). В качестве примера вычислим энтропии Н (Х), H (X | Y), H (X | yj) и взаимную информацию I (Х, У), когда системы А и В описываются двумерным распределением p (xi, yj), заданным в виде табл. 1. Вычисленные значения условной вероятности Используя записанные в таблицах значения вероятностей, полу чим
Отсюда
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 838; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.140.88 (0.009 с.) |

 или 2t + 1 ≤ d исправимы. Кратность ошибки – это количество единиц в векторе
или 2t + 1 ≤ d исправимы. Кратность ошибки – это количество единиц в векторе  .
.

 = 0, где
= 0, где 
 - проверочная матрица, а кодовое слово размера n –
- проверочная матрица, а кодовое слово размера n –  ). В этой системе уравнений количество строк m выбирается меньше количества столбцов для того, чтобы система уравнений имела не единственное решение, каждое из которых является разрешенным кодовым словом. Каждое из уравнений уменьшает количество независимых переменных xi на единицу. Поэтому количество независимых переменных, значения которых и место рас-положения можно выбирать произвольно, равно
). В этой системе уравнений количество строк m выбирается меньше количества столбцов для того, чтобы система уравнений имела не единственное решение, каждое из которых является разрешенным кодовым словом. Каждое из уравнений уменьшает количество независимых переменных xi на единицу. Поэтому количество независимых переменных, значения которых и место рас-положения можно выбирать произвольно, равно 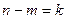 . Если в качестве неза-висимых переменных выбираются первые k символов x1,…,xk, то код называет-ся систематическим. Эти символы называются информационными в отличие от защитных xk+1,…,xn, причем защитные символы линейно выражаются через информационные. Таким образом, количество разрешенных кодовых слов равно 2k, а общее количество входных канальных кодовых слов равно 2n.
. Если в качестве неза-висимых переменных выбираются первые k символов x1,…,xk, то код называет-ся систематическим. Эти символы называются информационными в отличие от защитных xk+1,…,xn, причем защитные символы линейно выражаются через информационные. Таким образом, количество разрешенных кодовых слов равно 2k, а общее количество входных канальных кодовых слов равно 2n. ,
, и
и  по определению разрешенного кодового слова.
по определению разрешенного кодового слова. , где
, где  совпадает с разрешенным кодовым словом (
совпадает с разрешенным кодовым словом (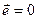 или
или  - слу-чай необнаружимой ошибки), то правая часть системы уравнений равна нулю:
- слу-чай необнаружимой ошибки), то правая часть системы уравнений равна нулю:  ,
,  , и отлична от нуля, когда
, и отлична от нуля, когда  . В общем случае
. В общем случае  , где вектор-столбец
, где вектор-столбец  называется синдромом.
называется синдромом.
 , т.к
, т.к  по определению разрешенного кодового слова
по определению разрешенного кодового слова  с минимальным весом. (Одно из значений синдрома равно нулю, когда вектор
с минимальным весом. (Одно из значений синдрома равно нулю, когда вектор  , которое являет-ся разрешенным.
, которое являет-ся разрешенным. и
и  .
. эквивалентны.
эквивалентны. , которое показывает, что расстояние между
, которое показывает, что расстояние между  и
и  , принадлежащих одному и тому же подмножеству, справедливы равенст-ва
, принадлежащих одному и тому же подмножеству, справедливы равенст-ва  и
и  . Складывая эти равенства и преобразуя суммы с учетом линейности системы уравнений (линейности оператора H) получим
. Складывая эти равенства и преобразуя суммы с учетом линейности системы уравнений (линейности оператора H) получим ,
, 
 является разрешенным кодовым словом по его определению, т.е. все векторы подмножества различаются между собой только на разрешенные кодовые слова.
является разрешенным кодовым словом по его определению, т.е. все векторы подмножества различаются между собой только на разрешенные кодовые слова. , а помеха
, а помеха  , действующего в канале. Механизм компенса-ции можно пояснить с помощью равенства:
, действующего в канале. Механизм компенса-ции можно пояснить с помощью равенства: .
. .
. поскольку pi удовлетворяет неравенству 0
поскольку pi удовлетворяет неравенству 0  1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что
1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что  pilog pi=0.
pilog pi=0. ) энтропия H(X)=logmx
) энтропия H(X)=logmx =1, можно выполнить следующие тождественные преобразования:
=1, можно выполнить следующие тождественные преобразования:
 воспользуемся неравенством lnz
воспользуемся неравенством lnz  z—1, положив z=
z—1, положив z= 
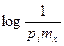 на
на  , получим
, получим

 .
. равна количеству информации,
равна количеству информации, является характеристикой источника сообщений и называется энтропией.
является характеристикой источника сообщений и называется энтропией. 1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что
1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что  ) энтропия H(X) max и определяется как H(X)=logmx
) энтропия H(X) max и определяется как H(X)=logmx
 воспользуемся неравенством lnz
воспользуемся неравенством lnz  на
на  , получим
, получим
 , изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций:
, изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций: ,
, конечна [9].
конечна [9]. называется ортогональной на отрезке [ a, b ], если
называется ортогональной на отрезке [ a, b ], если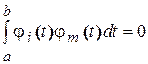 при
при 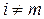 ,
, называется нормированной, если
называется нормированной, если .
. фиксированном числе членов ряда n значения коэффициентов
фиксированном числе членов ряда n значения коэффициентов  можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации (аппроксимация - приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач)
можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации (аппроксимация - приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач)
 .
. . Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами
. Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами 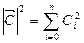 .
. .
.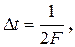 где F - верхняя граничная частота спектра сигнала. В этом случае функции
где F - верхняя граничная частота спектра сигнала. В этом случае функции ,
, , при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле
, при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле ,
, , то есть
, то есть 

 . (4)
. (4) ,
,
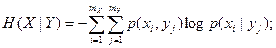


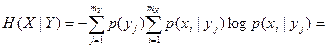

 называется частной условной энтропией. Она характеризует неопределенность состояния системы А в случае, когда известно состояние yj наблюдаемой системы В. Зафиксировав состояние yj системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие xi. Это обнаруживается как изменение вероятности реализации события xi (i =
называется частной условной энтропией. Она характеризует неопределенность состояния системы А в случае, когда известно состояние yj наблюдаемой системы В. Зафиксировав состояние yj системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие xi. Это обнаруживается как изменение вероятности реализации события xi (i =  ) (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности p (Xi), то после изменения условий она стала равной условной вероятности p (xi | yj). При отсутствии статистической зависимости H (X | yj)= H (X), поскольку P (xi | yj)= p (xi).
) (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности p (Xi), то после изменения условий она стала равной условной вероятности p (xi | yj). При отсутствии статистической зависимости H (X | yj)= H (X), поскольку P (xi | yj)= p (xi). X
y
X
y
 Таблица 2
Таблица 2 записаны в табл.2.
записаны в табл.2.











