
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейные системы автоматического управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 8.1. Особенности нелинейных систем Система автоматического регулирования является нелинейной, если для нее не выполняется принцип суперпозиции, и сигналы в системе связаны между собой нелинейными дифференциальными уравнениями. Строго говоря, линейных САУ не существует, так как характеристики реальных устройств нелинейны и некоторые из них не могут быть линеаризованы, а при больших отклонениях сигналов от установившихся значений приходится учитывать нелинейные свойства и элементов САУ, допускающих линеаризацию. Причиной нелинейности САУ может быть то, что некоторые сигналы или их производные входят в математическое описание системы не в первой степени или имеется произведение сигналов, а также то, что коэффициенты уравнений изменяются во времени или являются функциями сигналов и их производных. Очень часто нелинейность системы обусловлена наличием в ней звеньев, у которых выходной и входной сигналы связаны между собой существенной, т.е. неподдающейся линеаризации, статической нелинейной зависимостью вида: Во всех перечисленных случаях процессы, протекающие в САУ, описываются нелинейными дифференциальными уравнениями, что существенно усложняет их анализ. К сигналам в нелинейной системе неприменимы преобразования Лапласа или Фурье в обычном виде. В отличие от линейных САУ нелинейная система может иметь несколько состояний устойчивого или неустойчивого равновесия, причем области устойчивости определяются не только параметрами системы, но и значениями начальных условий. Нелинейная система может находиться не только в равновесно сходящемся процессе, но и в устойчивом установившемся периодическом режиме, называемом режимом автоколебаний. В переходном колебательном процессе в нелинейной системе изменяется не только амплитуда, но и частота колебаний. При описании нелинейных САУ сначала составляют дифференциальные уравнения для каждого звена системы. При этом характеристики звеньев, не являющихся существенно нелинейными, линеаризуются. В результате, получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы САУ, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть. Существует достаточно большое число методов, позволяющих решать задачи анализа и синтеза нелинейных систем, например: метод фазовой плоскости; метод кусочно-линейной аппроксимации; метод гармонической линеаризации; метод статистической линеаризации. Метод фазовой плоскости применяется для анализа нелинейных систем, порядок которых не выше второго. На плоскости с координатами Метод кусочно-линейной аппроксимации используется в том случае, когда нелинейная часть системы безынерционна, и ее характеристика может быть аппроксимирована прямолинейными участками. На каждом таком участке процессы в системе описываются линейными дифференциальными уравнениями, решение которых может быть найдено. В точках излома нелинейной характеристики решения «сшиваются»: значения переменных в конце данного участка принимаются за начальные условия для последующего участка. Таким образом удается построить фазовую траекторию движения системы. Метод гармонической линеаризации базируется на замене нелинейного элемента линейным звеном, параметры которого определяются при синусоидальном входном сигнале из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все гармонические составляющие выходного сигнала, кроме первой гармоники. Метод статистической линеаризации является приближенным и применим для систем произвольного порядка. Он основан на замене нелинейного элемента линейным звеном, коэффициенты передачи которого по математическому ожиданию и случайной составляющей сигнала на входе нелинейного элемента определяются из условия статистической эквивалентности нелинейного звена линейному звену. Рассмотрим описание динамики САУ на фазовой плоскости и использование метода гармонической линеаризации для широко распространенного класса нелинейных систем, характеризующегося следующими особенностями: 1) структура системы представляет собой соединения из двух частей (рис. 8.1) – линейной части (ЛЧ), описываемой линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами, и нелинейного элемента (НЭ); 2)
нелинейный элемент является безынерционным, и его входной  и выходной и выходной  сигналы связаны между собой некоторой статической зависимостью: сигналы связаны между собой некоторой статической зависимостью:
Если система содержит несколько нелинейных элементов, соединенных между собой параллельно, последовательно или по схеме обратной связи, то в ряде случаев удается заменить эти нелинейные элементы одним с результирующей статической характеристикой. На рис. 8.2, а приведена структура системы, состоящая из двух параллельно включенных нелинейных звеньев, а на рис. 8.2, б проиллюстрирована методика определения результирующей статической характеристики Рассмотрим структуру системы, состоящую из двух последовательно соединенных статических нелинейных звеньев (рис. 8.3, а). Методика построения результирующей нелинейной характеристики
Но удобнее построить эту характеристику в четвертом квадранте, для чего точка 3 с помощью биссектрисы третьего квадранта отображается в точку 4 на отрицательной полуоси ординат. Поскольку расстояния от начала координат до точек 3 и 4 одинаковы, точка 5 принадлежит эквивалентной нелинейной статической характеристике Наиболее просто строится характеристика последовательного соединения трех нелинейных звеньев. Характеристика В замкнутой системе (рис. 8.5, а) нелинейный элемент со статической нелинейностью
Проиллюстрируем методику построения результирующей характеристики такой системы (рис. 8.5, б). В первом квадранте строится характеристика 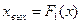 , а во втором (с поворотом осей на 900 против часовой стрелки) строится характеристика , а во втором (с поворотом осей на 900 против часовой стрелки) строится характеристика  . .
В случае отрицательной обратной связи
т.е. указанному значению выходного сигнала системы, соответствует входной сигнал равный:
Следовательно, для построения первой точки результирующей нелинейности системы Очевидно, что в случае положительной обратной связи, точку А необходимо было бы переносить на такое же расстояние влево. Осуществив указанную процедуру многократно, можно по полученным точкам построить результирующую характеристику: Если же между нелинейными элементами имеются разделяющие их инерционные линейные звенья, то САУ уже не удается свести к рассматриваемому в данном пособии классу систем. 8.2. Исследование нелинейных систем Метод фазовой плоскости используется для исследования нелинейных САУ, линейная часть которых с достаточной для решения практических задач точностью может быть описана дифференциальным уравнением второго порядка.
Фазовой плоскостью называется плоскость, на которой изображается изменение какой-либо переменной величины  в функции скорости ее изменения: в функции скорости ее изменения: 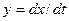 . Оси времени на фазовой плоскости нет, но каждому моменту времени соответствует определенная точка (изображающая точка), абсцисса и ордината которой равны соответственно значению сигнала и скорости его изменения в данный момент времени. При изменении времени изображающая точка перемещается по определенной траектории, называемой фазовой траекторией. . Оси времени на фазовой плоскости нет, но каждому моменту времени соответствует определенная точка (изображающая точка), абсцисса и ордината которой равны соответственно значению сигнала и скорости его изменения в данный момент времени. При изменении времени изображающая точка перемещается по определенной траектории, называемой фазовой траекторией.
Определим выражение фазовой траектории для сигнала
Скорость изменения такого сигнала равна:
Выражая из уравнений (8.1) и (8.2)
Следовательно, незатухающие гармонические колебания изображаются на фазовой плоскости в виде эллипса (рис. 8.6, б) с полуосями А и При изменении времени изображающая точка, будет перемещаться вдоль эллипса по часовой стрелке с периодом колебания Для различных амплитуд А при заданной частоте
Таким образом, по виду фазовой траектории можно наглядно судить об устойчивости системы. Возможно и решение обратной задачи – определение закона изменения сигнала
где
На рис. 8.9, а приведена совокупность таких фазовых траекторий, различающихся значениями абсциссы  и ординаты и ординаты 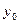 начальной точки для случая, когда знаки начальной точки для случая, когда знаки  и и 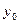 противоположны ( противоположны ( < 0), а на рис. 8.9, б – когда знаки < 0), а на рис. 8.9, б – когда знаки  и и 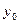 совпадают ( совпадают ( > 0). > 0).
Так как
Откуда
Совокупность графиков сигнала Аналитическое выражение для закона изменения сигнала
где
Рассмотрим общие закономерности, которым удовлетворяют фазовые траектории нелинейных систем. Поскольку в верхней полуплоскости фазовой плоскости Между собой фазовые траектории пересекаются только в особых точках. Особыми точками называют точки, соответствующие состоянию равновесия системы. Особые точки бывают четырех видов: центр, фокус, узел и седло. Центром называется особая точка в начале координат (на рис. 8.6, в). Особая точка в начале координат (см. рис. 8.7, в) является неустойчивым фокусом или устойчивым фокусом (см. рис. 8.8, в).
Начало координат является устойчивым узлом, если фазовые траектории входят в него (см. рис. 8.9, а), и неустойчивым узлом в противоположном случае (рис. 8.9, б). Находящаяся в начале координат особая точка типа «седло» всегда неустойчива, т.е. соответствует неустойчивому состоянию равновесия (рис. 8.11, а). На рис. 8.11, б особые точки образуют особый отрезок, в каждой точке которого возможно равновесие системы. Незатухающим колебаниям в нелинейной системе на фазовой плоскости соответствуют замкнутые траектории – предельные циклы. Они бывают устойчивыми и неустойчивыми. Устойчивый предельный цикл описывает на фазовой плоскости режим автоколебаний в системе. Он характерен тем, что фазовые траектории с обеих сторон от устойчивого предельного цикла «наматываются» на него (рис. 8.12, а). В случае неустойчивого предельного цикла фазовые траектории отдаляются от него с одной или с обеих сторон (рис. 8.12, б). Неустойчивый предельный цикл соответствует неустойчивым колебаниям, которые в реальных системах не существуют. При этом неустойчивый предельный цикл определяет на фазовой плоскости границу, разделяющую различные установившиеся режимы.
а статическая нелинейная зависимость между входным и выходным сигналом нелинейного элемента:
Такая статическая зависимость соответствует типовому нелинейному элементу «однозначная релейная характеристика с зоной нечувствительности».
Описание системы будем осуществлять в ее свободном движении, т.е. полагать, что  , при этом , при этом  . .
Изображение по Лапласу выходного сигнала системы равно:
Соответствующее выражению (8.7) операторное уравнение имеет вид:
или
Выполнив для (8.8) обратное преобразование Лапласа, получим:
В дальнейшем для упрощения аргумент t опускается. С учетом выражений (8.6) и (8.9) можно записать следующие дифференциальные уравнения, определяющие переходный процесс в системе в трех зонах величины
Наиболее просто выводится уравнение фазовой траектории для второй зоны (при
Разделив последнее выражение на равенство
Интегрируя последнее уравнение, находим:
где При различных значениях В первой зоне (при
С учетом
Разделив последнее уравнение на
Проинтегрировав это уравнение, получим:
где (
Подставляя в выражение (8.12) различные сочетания значений начальных условий Семейство фазовых траекторий для диапазона третьей зоны (
Для рассматриваемой системы все фазовые траектории, описываемые выражениями (8.12) – (8.13), имеют вид логарифмических спиралей, сходящихся к началу координат.
Далеко не всегда при исследовании системы на фазовой плоскости удается получить аналитическое выражение для фазовых траекторий. В то же время для любой системы, линейная часть которой описывается дифференциальным уравнением второго порядка, можно записать следующее уравнение:
которое может быть сведено к системе дифференциальных уравнений первого порядка:
Разделив первое уравнение системы (8.15) на второе, получим уравнение фазовой траектории в виде нелинейного дифференциального уравнения первого порядка:
Построение фазовых траекторий в общем случае не требует решения этого уравнения и может быть выполнено методом изоклин. С этой целью на фазовой плоскости строят семейство изоклин-линий, соответствующих алгебраическому уравнению
где Каждому значению С соответствует своя изоклина. Как следует из выражения (8.17) для каждой изоклины выполняется равенство:
т.е. изоклина представляет собой геометрическое место точек, в которых наклон фазовой траектории постоянен.
По фазовой картине САУ можно судить об устойчивости системы и характере переходных процессов ней. 8.3. Метод гармонической линеаризации При подаче на вход линейной системы гармонического сигнала
на выходе системы также устанавливается гармонический сигнал, но с другой амплитудой и смещенный по фазе по отношению к входному. Если же синусоидальный сигнал подать на вход нелинейного элемента, то на его выходе формируются периодические колебания, но по форме существенно отличающиеся от синусоидальных. В качестве примера на рис. 8.17 показан характер изменения выходной переменной Разлагая периодический сигнал на выходе нелинейного элемента в ряд Фурье, представляем
Выходной сигнал нелинейного элемента поступает на вход линейной части САУ (см. рис. 8.1), которая, как правило, обладает существенной инерционностью. При этом высокочастотные составляющие сигнала (8.19) практически не проходят на выход системы, т.е. линейная часть является фильтром по отношению к высокочастотным гармоническим составляющим. В связи с этим, а также учитывая, что амплитуды гармонических составляющих в Следовательно, при отсутствии постоянной составляющей в выходных колебаниях выражение (8.19) приближенно можно записать в виде:
Выражая из формулы (8.20) функцию
Таким образом, нелинейная зависимость выходной величины от входной в нелинейном элементе приближенно заменяется линейной зависимостью, описываемой выражением (8.21). Выполнив в выражении (8.21) преобразование Лапласа, получим:
Как и для непрерывных звеньев введем в рассмотрение передаточную функцию нелинейного гармонически линеаризованного элемента, как отношение изображения выходной величины к изображению входной величины:
Таблица 8.1
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.015 с.) |

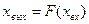 . К числу таких звеньев относятся так называемые типовые нелинейности (табл. 8.1).
. К числу таких звеньев относятся так называемые типовые нелинейности (табл. 8.1). , где
, где 
 .
.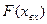 . Для ее построения достаточно сложить ординаты нелинейных характеристик
. Для ее построения достаточно сложить ординаты нелинейных характеристик  и
и  .
.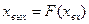 проиллюстрирована на рис. 8.3, б. В первом квадранте построена статическая характеристика первого нелинейного звена
проиллюстрирована на рис. 8.3, б. В первом квадранте построена статическая характеристика первого нелинейного звена 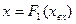 , а во втором квадранте – характеристика
, а во втором квадранте – характеристика  второгозвена, но так,
второгозвена, но так, 
 : ось
: ось  направлена по отрицательной полуоси абсцисс. Значению
направлена по отрицательной полуоси абсцисс. Значению 
 входного сигнала (точка 1 на оси
входного сигнала (точка 1 на оси 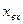 ) соответствует значение
) соответствует значение  на выходе первого нелинейного элемента (точка 2).
на выходе первого нелинейного элемента (точка 2).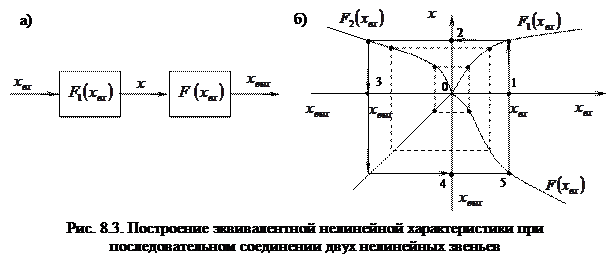
 (точка 3). Очевидно, что величины
(точка 3). Очевидно, что величины  представляют собой соответственно абсциссу и ординату одной из точек на результирующей нелинейной характеристике
представляют собой соответственно абсциссу и ординату одной из точек на результирующей нелинейной характеристике  располагается в первом квадранте, а характеристики
располагается в первом квадранте, а характеристики  и
и  , с соответствующим поворотом осей, – во втором и в третьем квадрантах (рис. 8.4).
, с соответствующим поворотом осей, – во втором и в третьем квадрантах (рис. 8.4).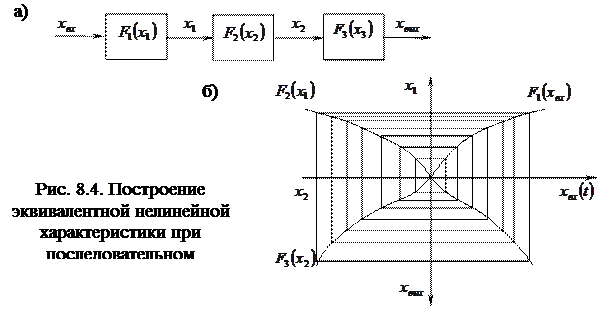
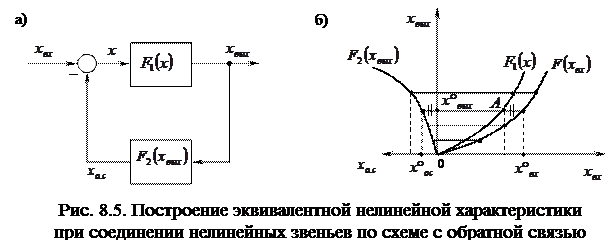
 ) – это соответствующие друг другу значения входного и выходного сигналов нелинейности в прямом канале системы. Сигнал
) – это соответствующие друг другу значения входного и выходного сигналов нелинейности в прямом канале системы. Сигнал  .
.
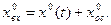

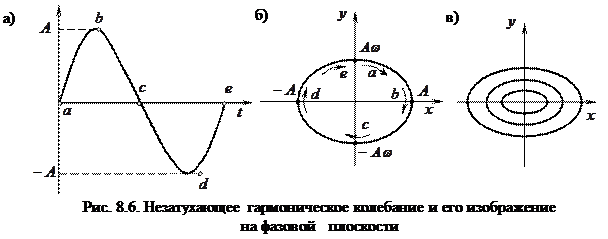
 и частотой
и частотой 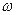 (рис. 8.6, а):
(рис. 8.6, а): . (8.1)
. (8.1) . (8.2)
. (8.2)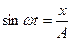 и
и  , на основании основного тригонометрического тождества получим:
, на основании основного тригонометрического тождества получим: . (8.3)
. (8.3) .
. .
.
 по уравнению фазовой траектории
по уравнению фазовой траектории  . Пусть, например, фазовая траектория представляет собой отрезок прямой, начальная точка (соответствующая моменту времени
. Пусть, например, фазовая траектория представляет собой отрезок прямой, начальная точка (соответствующая моменту времени  ) которого имеет координаты (
) которого имеет координаты ( ), а конечная совпадает с началом координат фазовой плоскости. Очевидно, что уравнение фазовой траектории:
), а конечная совпадает с началом координат фазовой плоскости. Очевидно, что уравнение фазовой траектории: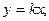

 .
.
 то уравнение фазовой траектории можно записать в виде:
то уравнение фазовой траектории можно записать в виде:  . Разделяя переменные, имеем
. Разделяя переменные, имеем  Интегрируя последнее выражение, получим:
Интегрируя последнее выражение, получим: =
= 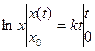 =
= 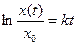 .
. и, следовательно, искомый закон изменения сигнала:
и, следовательно, искомый закон изменения сигнала: .
. ), отметить на фазовой траектории (рис. 8.10, а) точки, абсциссы которых отличаются друг от друга на достаточно малое постоянное по величине приращение
), отметить на фазовой траектории (рис. 8.10, а) точки, абсциссы которых отличаются друг от друга на достаточно малое постоянное по величине приращение  . При этом время перехода системы от одной такой точки к достаточно близкой соседней может быть приближенно определено по формуле:
. При этом время перехода системы от одной такой точки к достаточно близкой соседней может быть приближенно определено по формуле: , (8.4)
, (8.4)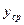 – среднее значение скорости изменения сигнала
– среднее значение скорости изменения сигнала  , находящейся на оси ординат (рис. 8.10, б).
, находящейся на оси ординат (рис. 8.10, б).
 , рассчитываемую для каждого перехода по выражению (8.4).
, рассчитываемую для каждого перехода по выражению (8.4).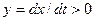 , то изображающая точка движется вдоль фазовой траектории в сторону увеличения
, то изображающая точка движется вдоль фазовой траектории в сторону увеличения  , следовательно, изображающая точка движется вдоль фазовой траектории в сторону уменьшения
, следовательно, изображающая точка движется вдоль фазовой траектории в сторону уменьшения 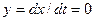 , то фазовые траектории пересекают ось х под прямым углом.
, то фазовые траектории пересекают ось х под прямым углом.

 ,(8.5)
,(8.5) (8.6)
(8.6)

 . (8.7)
. (8.7)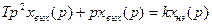
 (8.8)
(8.8) . (8.9)
. (8.9) (8.10)
(8.10) ). Так как
). Так как  и
и  , то дифференциальное уравнение для этой зоны можно записать следующим образом:
, то дифференциальное уравнение для этой зоны можно записать следующим образом: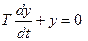 или
или  .
. или
или  .
. , (8.11)
, (8.11) – постоянная интегрирования.
– постоянная интегрирования. .
. ) дифференциальное уравнение, описывающее поведение системы, имеет вид:
) дифференциальное уравнение, описывающее поведение системы, имеет вид: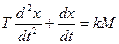 .
. или
или  .
. или
или  .
. . (8.12)
. (8.12)
 может быть найдена из начальных условий:
может быть найдена из начальных условий: ,
, ) – координаты точки, с которой начинается построение фазовой траектории:
) – координаты точки, с которой начинается построение фазовой траектории: .
. , получим семейство фазовых траекторий для диапазона значений регулируемой величины
, получим семейство фазовых траекторий для диапазона значений регулируемой величины  )получим из уравнения (8.12), заменив в нем величину M на – M:
)получим из уравнения (8.12), заменив в нем величину M на – M: . (8.13)
. (8.13) Полная фазовая картина процесса автоматического регулирования нелинейной системы, динамические свойства которой определяются дифференциальными уравнениями (8.10), имеет вид, представленный на рис. 8.14. Для других систем вид фазовых траекторий может быть иным. Например, на рис. 8.15 изображена фазовая картина для нелинейной системы с той же передаточной функцией линейной части, что и в предыдущем примере, но для случая, когда включенный в систему релейный элемент не имеет зоны нечувствительности, т.е.
Полная фазовая картина процесса автоматического регулирования нелинейной системы, динамические свойства которой определяются дифференциальными уравнениями (8.10), имеет вид, представленный на рис. 8.14. Для других систем вид фазовых траекторий может быть иным. Например, на рис. 8.15 изображена фазовая картина для нелинейной системы с той же передаточной функцией линейной части, что и в предыдущем примере, но для случая, когда включенный в систему релейный элемент не имеет зоны нечувствительности, т.е. (8.14)
(8.14)
 (8.15)
(8.15) . (8.16)
. (8.16) , (8.17)
, (8.17) – постоянная величина, для которой задается ряд произвольных значений от –
– постоянная величина, для которой задается ряд произвольных значений от – 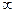 до +
до +  ,
,
 , проводятся два луча с наклонами, соответствующими значениям
, проводятся два луча с наклонами, соответствующими значениям  ) – очередная точка фазовой траектории, из которой осуществляются аналогичные построения.
) – очередная точка фазовой траектории, из которой осуществляются аналогичные построения. (8.18)
(8.18) нелинейного элемента с релейной характеристикой (8.14) при поступлении на его вход синусоидальных колебаний (8.18).
нелинейного элемента с релейной характеристикой (8.14) при поступлении на его вход синусоидальных колебаний (8.18).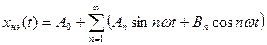 , (8.19)
, (8.19)
 – постоянные коэффициенты ряда Фурье;
– постоянные коэффициенты ряда Фурье;  – частота колебаний первой гармоники (основная частота), равная частоте входных синусоидальных колебаний; Т – период колебания первой гармоники, равный периоду входных синусоидальных колебаний.
– частота колебаний первой гармоники (основная частота), равная частоте входных синусоидальных колебаний; Т – период колебания первой гармоники, равный периоду входных синусоидальных колебаний. . (8.20)
. (8.20) , а из производной
, а из производной  – функцию
– функцию  , преобразуем выражение (8.20) следующим образом:
, преобразуем выражение (8.20) следующим образом: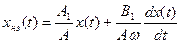 . (8.21)
. (8.21)
 . (8.22)
. (8.22)


