
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательные корректирующие устройстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В соответствии с выражением (7.1) АФХ разомкнутой скорректированной системы равна:
а логарифмические амплитудно- и фазо-частотные характеристики соответственно:
Из выражений (7.6) и (7.7) следует, что амплитудно- и фазо-частотные характеристики последовательно корректирующего звена равны:
В качестве примера на рис.7.7 приведены логарифмические частотные характеристики разомкнутой нескорректированной системы (
с дифференцирующими свойствами в среднечастотном диапазоне (
Значения сопрягающих частот
Для уточнения действительного запаса устойчивости по модулю и фазе синтезированной системы на рис.7.7 построена логарифмическая фазо-частотная характеристика 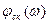 . Как видно из рис. 7.7, запасы устойчивости по фазе и по модулю скорректированной системы больше соответствующих запасов устойчивости исходной системы. . Как видно из рис. 7.7, запасы устойчивости по фазе и по модулю скорректированной системы больше соответствующих запасов устойчивости исходной системы.
Из рассмотренного примера следует, что достоинство коррекции с помощью последовательных дифференцирующих устройств заключается в том, что при обеспечении требуемого запаса устойчивости одновременно увеличивается частота среза Однако последовательная коррекция с помощью дифференцирующих устройств имеет и недостатки, заключающиеся в значительном увеличении усиления в области высоких частот. Если при этом на полезный входной сигнал системы накладываются высокочастотные помехи, степень их подавления в скорректированной системе будет ниже, чем в нескорректированной. Помехоустойчивость системы может быть повышена путем снижения коэффициента усиления системы, но это приведет к снижению точности регулирования. Для исключения существенного ослабления коэффициента усиления системы на низких частотах в качестве последовательного корректирующего звена можно использовать интегро-дифференцирующее звено с преобладающими интегрирующими свойствами, т.е. при Как видно из рис. 7.8, исходная нескорректированная система не только не обеспечивает требуемого качества регулирования, но даже является неустойчивой. Без корректирующего устройства требуемый запас устойчивости в системе можно обеспечить только за счет большого снижения коэффициента усиления системы, что является нежелательным. Желаемую ЛАХ скорректированной системы можно получить при последовательном включении корректирующего устройства с интегрирующими свойствами. Из рис. 7.8 следует, что наряду с относительным увеличением коэффициента усиления системы на низких частотах существенно уменьшено усиление на высоких частотах и тем самым ослаблено влияние высокочастотных помех.
При решении практических инженерных задач по синтезу структуры САУ широкое применение находят последовательные корректирующие устройства в виде комбинированных интегро-дифференцирующих звеньев. Пример синтеза желаемых логарифмических частотных характеристик системы с помощью последовательного комбинированного интегро-дифференцирующего звена представлен на рис. 7.9. Из рис. 7.9 следует, что при правильно выбранных параметрах корректирующего устройства можно обеспечить требуемую точность регулирования в установившихся режимах и одновременно повысить качество переходного процесса, по сравнению с исходной системой. Передаточная функция корректирующего звена с ЛАХ
При выборе коэффициента усиления корректирующего устройства
Постоянные времени корректирующего устройства Частоты сопряжения Зачастую не все из перечисленных рекомендаций по выбору параметров корректирующего устройства удается удовлетворить в полной мере. Поэтому необходимо построить ЛАХ скорректированной системы с учетом фактических логарифмических частотных характеристик корректирующего устройства и проверить, например, путем моделирования системы на ЭВМ, удовлетворяет ли САУ предъявляемым требованиям к качеству регулирования.
|
|||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.10.80 (0.01 с.) |

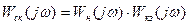 , (7.5)
, (7.5)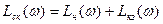 ; (7.6)
; (7.6)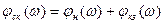 . (7.7)
. (7.7)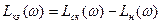 ; (7.8)
; (7.8)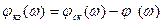 . (7.9)
. (7.9)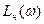 и
и 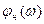 ). На этом же рисунке представлена желаемая ЛАХ скорректированной системы
). На этом же рисунке представлена желаемая ЛАХ скорректированной системы 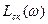 и соответствующая ей фазо-частотная характеристика
и соответствующая ей фазо-частотная характеристика 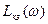 . Приведенная на рис.7.7
. Приведенная на рис.7.7 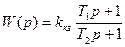
 >
> 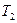 ). Параметры корректирующего звена определяются следующим образом:
). Параметры корректирующего звена определяются следующим образом: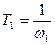 ;
; 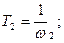
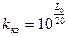 .
.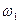 и
и 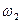 , а также величина
, а также величина 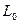 берутся из рис. 7.7.
берутся из рис. 7.7.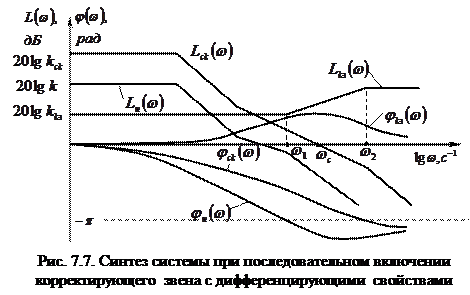
 и возможно увеличение коэффициента усиления системы, в результате чего уменьшаются время регулирования и установившаяся ошибка.
и возможно увеличение коэффициента усиления системы, в результате чего уменьшаются время регулирования и установившаяся ошибка.
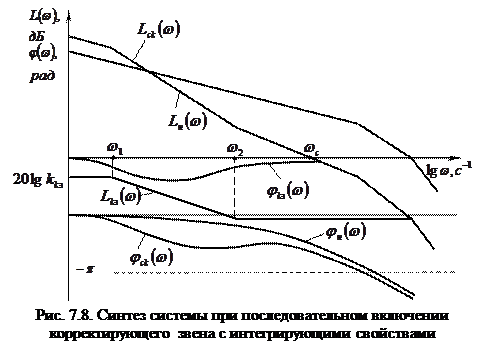
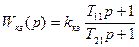
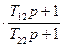 .
.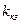 следует исходить из условия обеспечения требуемой точности в установившихся режимах скорректированной системы. Так, если коэффициент передачи исходной нескорректированной разомкнутой системы равен
следует исходить из условия обеспечения требуемой точности в установившихся режимах скорректированной системы. Так, если коэффициент передачи исходной нескорректированной разомкнутой системы равен 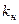 , атребуемый коэффициент передачи скорректированной системы равен
, атребуемый коэффициент передачи скорректированной системы равен 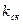 , то коэффициент передачи корректирующего устройства должен быть равен:
, то коэффициент передачи корректирующего устройства должен быть равен: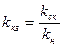 .
.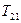 и
и 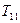 необходимо выбирать так, чтобы частоты сопряжения
необходимо выбирать так, чтобы частоты сопряжения 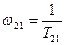 и
и 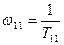 были бы значительно меньше частоты среза
были бы значительно меньше частоты среза 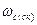 скорректированной системы. Этим обеспечивается сдвиг интервала частот, в котором корректирующее устройство создает отставание по фазе в безопасную зону слева от частоты среза.
скорректированной системы. Этим обеспечивается сдвиг интервала частот, в котором корректирующее устройство создает отставание по фазе в безопасную зону слева от частоты среза.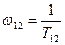 и
и 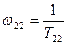 должны быть такими, чтобы частота среза
должны быть такими, чтобы частота среза 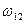 <
< 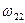 . В этом случае максимальное опережение, создаваемое корректирующим устройством, будет в области частоты среза, что обеспечивает в скорректированной системе наибольший запас устойчивости по фазе.
. В этом случае максимальное опережение, создаваемое корректирующим устройством, будет в области частоты среза, что обеспечивает в скорректированной системе наибольший запас устойчивости по фазе.


