
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерционное звено второго порядкаСодержание книги
Поиск на нашем сайте
Инерционное звено второго порядка – это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением:
Операторное уравнение звена:
Передаточная функция звена:
Примерами реализации инерционного звена второго порядка являются RLC-контур, состоящий из катушки индуктивности, резистора и конденсатора, или физический маятник. Амплитудно- и фазо-частотная характеристики: A(ω) В зависимости от значения коэффициента демпфирования 1) Консервативное звено:
При этом ее полюса чисто мнимые: В соответствии с (2.15) и (2.23) выражения переходной функции и функции веса консервативного звена:
2) Колебательное звено:
Кусочно-асимптотическая ЛАЧХ звена состоит из двух участков. На низкочастотном участке до частоты сопряжения
а в диапазоне частот много больше частоты сопряжения уравнение высокочастотной асимптоты:
Последнее уравнение – это уравнение прямой с наклоном -40 дБ/дек. В окрестности частоты сопряжения график ЛАЧХ колебательного звена при Выражения переходной функции и функции веса колебательного звена:
где 3) Апериодическое звено второго порядка:
Очевидно, что между коэффициентами передаточных функций (2.51) и (2.54) существуют следующие зависимости:
 и и  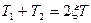 . .
Уравнения логарифмических амплитудно- и фазо-частотной характеристик:
Графики логарифмических амплитудно- и фазочастотной характеристик инерционного звена второго порядка для различных значений коэффициента демпфирования приведены на рис. 2.18; графики временных характеристик – на рис. 2.19. Звено чистого запаздывания Звено чистого запаздывания – это звено, выходной сигнал которого полностью совпадает по форме с входным сигналом, но отстает от него на время
На основании теоремы запаздывания (2.11):
где Частотные характеристики для звена чистого запаздывания:
т.е. P(ω) = cos(ω) и Q(ω)= – sin (ω); A(ω) = 1, На рис.2.20 приведен график переходной функции звена, на рис.2.21 – годограф АФХ, а на рис. 2.22 – логарифмические амплитудно- и фазо-частотные характеристики. Интегро-дифференцирующее звено Интегро-дифференцирующее звено порядка – это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением:
Операторное уравнение звена:
Передаточная функция звена
Частотные характеристики:
Выполнив несложные преобразования, можно представить АФХ звена в виде функции, связывающей вещественную
где
Вид всех остальных характеристик интегро-дифференцирующего звена также определяется соотношением между постоянными времени T1 и T2: A(ω)=
Воспользуемся формулой разложения (2.15) для получения выражение переходной функции интегро-дифференцирующего звена.
Изображение по Лапласу переходной функции:
В соответствии с выражением (2.15):
Следовательно, переходная функция интегро-дифференцирующего звена (рис. 2.25) имеет вид:
Пропорционально-интегральный регулятор (ПИ-регулятор) Пропорционально-интегральный регулятор (ПИ-регулятор) – это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением:
Операторное уравнение звена:
Передаточная функция звена
Следовательно, изображение по Лапласу сигнала на выходе звена представляет собой сумму двух составляющих, одна из которых пропорциональна входному сигналу, а вторая – пропорциональна интегралу от входного сигнала, что и определяет название данного звена:
Частотные характеристики ПИ-регулятора:
Переходная функция звена (рис. 2.27):
Неминимально-фазовые звенья Мы рассмотрели наиболее часто встречающиеся на практике типы минимально-фазовых звеньев. В отличие от них передаточная функция любого неминимально-фазового звена имеет хотя бы один «правый» ноль или полюс. Приведем пример такой передаточной функции:
Здесь имеется положительный полюс (корень знаменателя):
Частотные характеристики такого звена:
так как при В то же время для обычного апериодического звена имеем:
Разница между ними, как видим, в величине фазы, амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудно-частотной характеристике всегда можно определить амплитудно-фазовую и наоборот. Этим же свойством обладают вещественная Заметим, что для данного неминимально-фазового звена переходная функция будет расходящейся, вместо обычной затухающей. 2.6. Эквивалентные преобразования структурных схем линейных САУ В САУ встречаются три вида соединений звеньев: последовательное, параллельное и соединение звеньев по схеме с обратной связью. В системе, состоящей из n последовательно соединенных звеньев (рис. 2.28) выходной сигнал предыдущего звена равен входному сигналу последующего.
xвых1(p) = W1(p)xвх(p); xвых 2 (p) = W2(p) xвых 1 (p); … xвых(p) = Wn(p)xвых(n)(p).
Откуда xвых Следовательно, передаточная функция системы примет вид:
Таким образом, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев. Частотные характеристики последовательно соединенных звеньев:
где A(ω) = A1(ω)A2(ω)…An(ω); Логарифмическая амплитудно-частотная характеристика звеньев, соединенных последовательно:
Следовательно, логарифмические амплитудно- и фазо-частотная характеристики системы, состоящей из последовательно соединенных звеньев, равны сумме ЛАХ и ФЧХ отдельных звеньев. Это существенно упрощает построение логарифмических частотных характеристик, по сравнению с обычными характеристиками.
Передаточная функция минимально-фазовой системы в общем случае может быть записана в виде:
В выражении (2.59) сомножители в числителе · сомножитель · сомножитель · сомножитель Аналогичные сомножители в знаменателе выражения (2.59) · сомножитель · сомножитель · сомножитель Очевидно, что в зависимости от соотношения s и Формально передаточная функция (2.59) представляет собой произведение нескольких сомножителей, что соответствует последовательному соединению звеньев, и для вычисления На оси частот в порядке возрастания указываются все частоты сопряжения Построение ЛАХ начинается на частотах, меньших самой малой частоты сопряжения Если при этом в выражении (2.59) выполняется равенство s = Если в выражении (2.59) s
т.е. ЛАХ до наименьшей частоты сопряжения Если в выражении (2.48) s =
и наклон ЛАХ до наименьшей частоты сопряжения Для построения низкочастотной асимптоты ЛАХ необходимо для произвольной частоты
На частоте
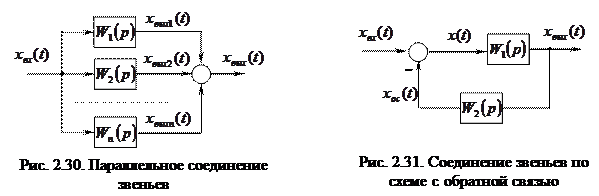
Если сомножитель вида В случае, когда Таким же образом характеристика продолжается в сторону увеличения частоты, претерпевая соответствующие изломы на каждой сопрягающей частоте Примеры построения ЛАХ по различным передаточным функциям приведены на рис. 2.29. В системе, состоящей из n параллельно соединенных звеньев (рис. 2.30), на вход каждому из звеньев подается один и тот же сигнал xвх(p), а их выходные сигналы суммируются:
Так как
……………………………
то
xвых(p) = xвых 1 (p) +xвых 2 (p)+…+xвых(n)(p) =  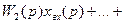  . .
Таким образом, передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев: W(p) = Очевидно, что в случае, когда выходной сигнал какого-либо из параллельно соединенных звеньев поступает в сумматор со знаком «минус», передаточная функция этого звена входит в (2.62) также со знаком «минус». Рассмотрим структуру системы с обратной связью (рис. 2.31). На вход звена, охваченного обратной связью, подается сигнал рассогласования, равный:
Поскольку Изображение выходного сигнала: xвых(р)= откуда
Следовательно, передаточная функция замкнутой системы (в замкнутом состоянии) описывается следующим выражением: Ф(p) = Передаточная функция (2.63) найдена для случая отрицательной обратной связи. Если обратная связь положительная, то Ф(p) = При анализе и синтезе CАУ, наряду с передаточной функцией (2.63) – (2.64), используются передаточная функция разомкнутой системы и передаточная функция по ошибке. Передаточная функция разомкнутой системы (замкнутой системы в разомкнутом состоянии): W(p) = Передаточная функция по ошибке: Фx(p) =
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 3169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.29.0 (0.012 с.) |



 - коэффициент демпфирования.
- коэффициент демпфирования.
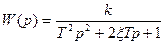 . (2.51)
. (2.51) ;
;  . (2.52)
. (2.52) , передаточная функция (2.51) принимает вид:
, передаточная функция (2.51) принимает вид: . (2.53)
. (2.53)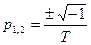 .
.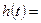
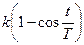 ;
; 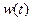 =
= 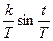 .
.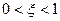 , полюса передаточной функции (2.51) – комплексно-сопряженные числа. С учетом (2.52) логарифмическая амплитудно-частотная характеристика звена примет вид:
, полюса передаточной функции (2.51) – комплексно-сопряженные числа. С учетом (2.52) логарифмическая амплитудно-частотная характеристика звена примет вид: .
. уравнение горизонтальной асимптоты:
уравнение горизонтальной асимптоты: ,
,
 имеет амплитудный всплеск («горб»), величина которого тем больше, чем меньше коэффициент демпфирования
имеет амплитудный всплеск («горб»), величина которого тем больше, чем меньше коэффициент демпфирования  ;
; ;
; .
. , полюса передаточной функции (2.51) – действительные числа, поэтому передаточную функцию звена можно представить в следующем виде:
, полюса передаточной функции (2.51) – действительные числа, поэтому передаточную функцию звена можно представить в следующем виде: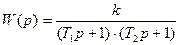 . (2.54)
. (2.54)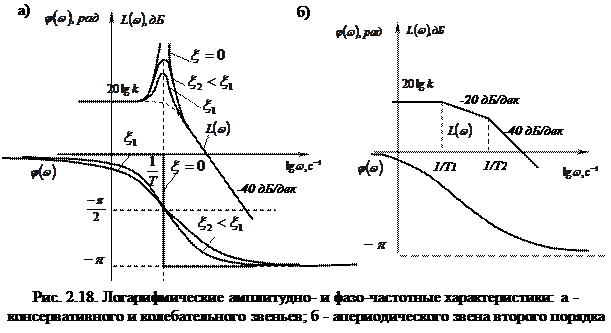
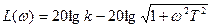
 ;
;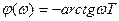
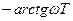 .
.
 ;
; .
. , т.е.
, т.е. .
.
 . Следовательно, передаточная функция звена имеет вид:
. Следовательно, передаточная функция звена имеет вид: ,
, cos(ω) – j sin (ω);
cos(ω) – j sin (ω); ω
ω 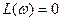 .
.

 .
. .
. ;
;  ;
;  ; (2.55)
; (2.55) и мнимую
и мнимую  частотные характеристики:
частотные характеристики: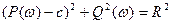 , (2.56)
, (2.56) ;
; 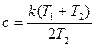 .
.
 , центр которой находится на действительной положительной полуоси в точке
, центр которой находится на действительной положительной полуоси в точке  . При этом годограф
. При этом годограф 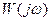 расположен в первом квадранте, если T1 > T2 (рис. 2.32, а), и в четвертом квадранте, если T1 <T2 (рис. 2.32, б).
расположен в первом квадранте, если T1 > T2 (рис. 2.32, а), и в четвертом квадранте, если T1 <T2 (рис. 2.32, б). =
=  ;
; ;
; .
.
 >
> 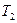 в среднечастотном диапазоне преобладают дифференцирующие свойства звена (наклон ЛАХ +20дБ/дек), а при
в среднечастотном диапазоне преобладают дифференцирующие свойства звена (наклон ЛАХ +20дБ/дек), а при 
 ;
;  ;
;  ;
; ;
;  ;
; 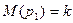 ;
;  ;
; и
и 


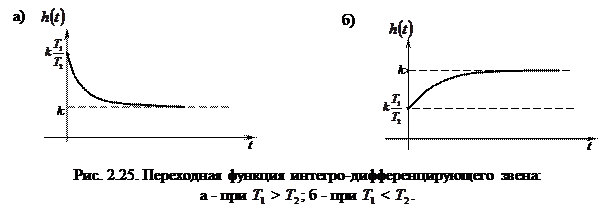

 .
. .
. .
. ;
; 
 ;
;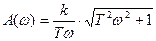 ;
;  ;
;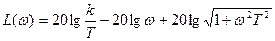 .
.
 .
.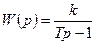 .
.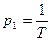 .
.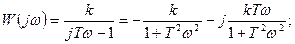
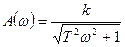 ;
; 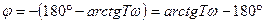 ,
, входной и выходной гармонические сигналы находятся в противофазе.
входной и выходной гармонические сигналы находятся в противофазе.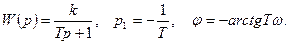
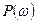 и мнимая
и мнимая 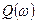 части амплитудно-фазовой характеристики минимально-фазовых звеньев.
части амплитудно-фазовой характеристики минимально-фазовых звеньев.
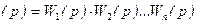 xвх(p).
xвх(p).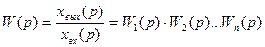 . (2.57)
. (2.57)
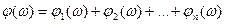 .
.
 . (2.58)
. (2.58)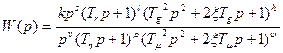 . (2.59)
. (2.59)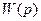 определяют нули передаточной функции, а именно:
определяют нули передаточной функции, а именно: соответствует нулевому нолю кратности
соответствует нулевому нолю кратности 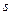 ,
,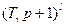 – действительному нолю
– действительному нолю 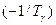 кратности l,
кратности l, – паре комплексно-сопряженных нолей кратности
– паре комплексно-сопряженных нолей кратности 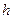 .
.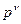 соответствует нулевому полюсу кратности
соответствует нулевому полюсу кратности 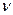 ,
,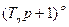 – действительному полюсу
– действительному полюсу  кратности
кратности 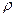 ,
, – паре комплексно-сопряженных полюсов кратности
– паре комплексно-сопряженных полюсов кратности 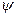 .
.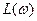 можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.
можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.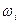 ЛАХ, определяемые соответствующими постоянными времени:
ЛАХ, определяемые соответствующими постоянными времени: 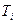 .
.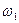 .
.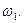
 , а
, а  , (2.60)
, (2.60)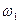 проводится с наклоном (+20∙ s) дБ/дек.
проводится с наклоном (+20∙ s) дБ/дек. , а
, а 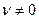 , то уравнение низкочастотной асимптоты:
, то уравнение низкочастотной асимптоты: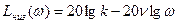 , (2.61)
, (2.61)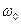 меньшей или равной
меньшей или равной 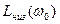 и через точку с координатами (
и через точку с координатами (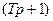 в числителе передаточной функции (2.59).
в числителе передаточной функции (2.59).
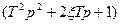 , происходит изменение предыдущего наклона на +40∙ h, если указанный сомножитель присутствует в числителе
, происходит изменение предыдущего наклона на +40∙ h, если указанный сомножитель присутствует в числителе 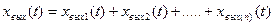 .
. ;
;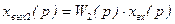 ;
;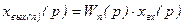 ,
,
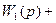
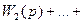
 . (2.62)
. (2.62)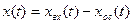 .
.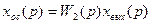 , то
, то 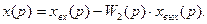
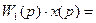

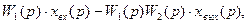
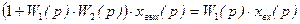 .
.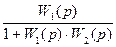 . (2.63)
. (2.63)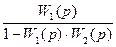 . (2.64)
. (2.64) . (2.65)
. (2.65)

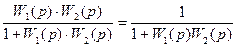 . (2.66)
. (2.66)


