
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы комбинированного управленияСодержание книги
Поиск на нашем сайте Использование принципа комбинированного управления, наряду с отмеченными подходами, позволяет повысить точность САУ. В системах, построенных по этому принципу, управляющее воздействие на объект управления зависит как от ошибки регулирования, так от внешнего воздействия. Теоретически в системах с комбинированным управлением величину установившейся ошибки можно свести к нулю при произвольном внешнем воздействии. Это свойство называется инвариантностью системы по отношению к внешнему воздействию. Поскольку внешним воздействием на систему может быть как управляющий, так и возмущающий сигнал, различают системы инвариантные по управлению и по возмущению. Передаточная функция системы комбинированного управления по управляющему воздействию (рис. 5.3): Ф(р) = Передаточная функция этой системы без учета канала комбинированного управления (полагая Wк(р) = 0): ФбезКУ(р) =
Характеристические полиномы передаточных функций (5.3) и (5.4) совпадают, на основании чего можно сделать заключение о совпадении их полюсов. Следовательно, введение канала комбинированного управления, в отличие от рассмотренных методов, не влияет на устойчивость системы. Передаточная функция системы комбинированного управления по ошибке:
Очевидно, что в том случае, когда передаточная функции канала комбинированного управления равна:
передаточная функция (5.5), а следовательно, и ошибка регулирования в системе при любой форме управляющего воздействия будет равняется нулю. Такая инвариантность называется абсолютной (полной). Рассмотрим в качестве примера систему комбинированного управления по управляющему воздействию (см. рис. 5.3), в которой
Передаточная функция такой системы по ошибке равна:
Рассматриваемая система – астатическая с астатизмом первого порядка. Передаточная функция канала комбинированного управления для обеспечения полной инвариантности согласно выражению (5.6) должна быть равна:
где Изображение по Лапласу сигнала
и с учетом выражения (5.8) изображение сигнала в канале комбинированного управления равно:
а соответствующий ему оригинал:
Следовательно, сигнал, подаваемый в систему по каналу комбинированного управления, равен сумме двух составляющих, пропорциональных производным управляющего сигнала по времени, соответственно первого и второй порядка. Порядок передаточной функции Практическое использование принципа комбинированного управления ограничено тем, что в реальных технических САУ на полезные сигналы накладываются высокочастотные помехи. При этом выполнение операции дифференцирования приводит к увеличению уровня помех, возрастающего по мере увеличения порядка производной. Понизив порядок старшей производной до значения, приемлемого по соображениям помехоустойчивости, можно обеспечить частичную инвариантность системы, что позволяет существенно уменьшить ошибку системы регулирования. Если в рассмотренном примере ограничиться только первой производной управляющего воздействия, т.е. подавать в систему по каналу комбинированного управления сигнал
получим, что
На основании сравнения выражений (5.7) и (5.9) можно сделать заключение, что порядок астатизма системы увеличился с первого до второго без снижения ее устойчивости.
Фх(р) = С целью обеспечения абсолютной инвариантности по возмущению передаточная функция звена в канале комбинированного управления должна быть равной:
И в этом случае на практике ограничиваются частичной инвариантностью, если точное удовлетворение условию вызывает технические трудности. При обеспечении инвариантности по возмущению особая трудность заключается в том, что возмущающие воздействия Вопросы для самопроверки 1. По каким характеристикам САУ может быть осуществлена их классификация на статические и астатические? 2. Укажите, как определить порядок астатизма системы по 3. Чему равна ошибка по скорости в астатической системе с астатизмом второго порядка? 4. Назовите основные методы, обеспечивающие повышение точности САУ. 5. Как влияет использование комбинированного управления на устойчивость САУ? 6. С чем связано ограничение, обусловливающее невозможность достижения абсолютной инвариантности системы?
|
|||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

 . (5.3)
. (5.3) . (5.4)
. (5.4)
 . (5.5)
. (5.5) ,(5.6)
,(5.6) и
и  .
.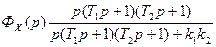 . (5.7)
. (5.7)
 (5.8)
(5.8)
 на выходе звена с передаточной функцией
на выходе звена с передаточной функцией 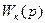 равно:
равно: ,
,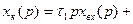



 может быть гораздо выше второго, что приведет к необходимости многократного дифференцирования управляющего сигнала.
может быть гораздо выше второго, что приведет к необходимости многократного дифференцирования управляющего сигнала. ,
,
 . При этом, в соответствии с выражением (5.5), передаточная функция системы по ошибке будет равна:
. При этом, в соответствии с выражением (5.5), передаточная функция системы по ошибке будет равна: . (5.9)
. (5.9)

 . (5.10)
. (5.10) . (5.11)
. (5.11)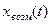 в отличие от задающихдалеко не всегда можно подать на вход
в отличие от задающихдалеко не всегда можно подать на вход 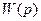 ; по Фх(р); по значениям коэффициентов ошибки.
; по Фх(р); по значениям коэффициентов ошибки.


