
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенная структурная схема САУСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ Теория автоматического управления изучает процессы управления, методы исследования и основы проектирования систем автоматического управления (САУ). Понимая управление каким-либо объектом, как процесс воздействия на него с целью обеспечения требуемого изменения его состояния, под автоматическим управлением будем понимать управление объектом без непосредственного участия человека. В настоящее время теория автоматического управления представляет собой единую научную базу для решения задач управления объектами различной природы: физической, химической, биологической и т.п. Целью проведения инженерных расчетов САУ является решение одной из двух задач – анализа или синтеза системы. В первом случае требуется оценить показатели качества регулирования системы при условии, что ее структура и значения параметров известны. Во втором случае задаются требуемые значения показателей качества и ставится задача создать систему, удовлетворяющую этим требованиям. Независимо от цели расчетов решение поставленной задачи предполагает разработку математического описания системы – ее математической модели. 1. ОСНОВНые понятия и определения теории автоматического управления 1.1. Краткие сведения по истории развития систем автоматического управления К числу определяющих моментов в истории развития систем автоматического управления обычно относят создание центробежного регулятора, запатентованного Дж. Уаттом в 1784 году, и предназначенного для регулирования скорости паровой машины. Регулирование осуществлялось двумя сбалансированными на одной оси грузами, вращающимися синхронно с валом машины и соединенными с дроссельной заслонкой, которая при центробежном перемещении грузов перекрывала проходное сечение парового патрубка. Установка паровой машины Дж.Уатта на транспортные объекты (повозки и корабли) привела к созданию паровозов и пароходов, что привело к появлению транспортного машиностроения. Но очевидно, что потребность в использовании различного рода регуляторов возникла гораздо раньше – а именно при создании таких высокоточных механизмов, как часы. Сохранилось описание конструкции часов, которые Гюйгенс в 1657 году снабдил маятниковым регулятором хода. Гораздо более раннее упоминание об использовании автоматических устройств связано с именем Герона Александрийского, в работах которого рассматривается пневматическое устройство, предназначенное для автоматического открывания ворот храма, но которое так и не было реализовано практически. И лишь на рубеже XVIII и XIX столетий, в эпоху бурного развития промышленности в Европе началось широкое внедрение промышленных регуляторов. К первым автоматическими регуляторами этого периода, кроме упомянутого регулятора скорости Дж. Уатт, следует отнести автоматический поплавковый регулятор питания котла паровой машины, внедренный в 1765 году И.И. Ползуновым, то есть почти на двадцать лет раньше регулятора Уатта, а также система программного управления ткацким станком, разработанная Жаккаром в 1804-1808 годах. В этот же период начинает развиваться и теория автоматического управления, формируется ряд важных принципов автоматики: принцип регулирования по отклонению Ползунова-Уатта и принцип регулирования по возмущению Понселе. Первые публикации по исследованию регуляторов появляются в двадцатых–тридцатых годах XIX века. Д.С. Чижов опубликовал один из первых трудов в 1823 году. Значительный вклад в теорию внесли три фундаментальные работы, содержащие по существу изложение основ новой науки: Д.К. Максвелла «О регуляторах» (1866 г.) и две работы И.А. Вышнеградского «Об общей теории регуляторов» (1876 г.) и «О регуляторах прямого действия» (1877 г.). Их публикация позволило дать общий подход к исследованию разнообразных по своей физической природе систем, заложить основы теории устойчивости и установить ряд важных общих закономерностей регулирования по принципу обратной связи. Начинается усиленная разработка математического аппарата, в частности были разработаны алгоритм для определения устойчивости систем по виду корней характеристического уравнения и критерии устойчивости систем Раусcа (1877 год) и Гурвица (1895 год). В 1892 г. выходит в свет работа А.М. Ляпунова "Общая задача об устойчивости движения", окончательно сформулировавшая теорию регулирования как особую область знаний, опирающуюся на строго доказанный математический аппарат и конкретные практические приложения. Важное место в теории регулирования занимают работы Н.Е. Жуковского «О прочности хода» и «Теория регулирования хода машин» (1909 г.). В период с 1900 по 1940 гг. появляется целый ряд работ, рассматривающих приложения теории регулирования к разнообразным техническим процессам. Особенно чётко мысль о теории регулирования как о дисциплине общетехнического характера проводится в ряде работ И.И. Вознесенского (период с 1922 по 1942 гг.), руководителя одной из крупнейших научных школ в этой области. Быстрое развитие систем автоматического управления вело к необходимости создания более эффективных методов исследования. Появляются работы Найквиста (1932 г.) и Михайлова (1938 г.), касающиеся теории устойчивости. Частотные критерии устойчивости, разработанные А.В. Михайловым, быстро вошли в практику. В 1946 г. Т Броде и Я. Маккол ввели в рассмотрение логарифмические характеристики. В эти же годы усилия исследователей направляются на разработку общих основ теории нелинейных систем. Одно из важнейших направлений, исследование устойчивости нелинейных систем, основывающееся на работах А.М. Ляпунова (1896 г.), развивалось в работах Н.Г. Четаева (1945 г.), А.И. Лурье (1944–1951), А.М. Летова и др. В трудах Г.В. Щипанова, В.С. Кулебякина, Б.Н. Петрова и других были разработаны теория автоматического регулирования по возмущению и теория компенсации возмущений. В.В. Казаничевым, А.П. Юркевичем, А.А. Фелдбаумом, А.А. Красовским и другими были сформулированы и исследованы принципы экстремального управления и разработана теория экстремальных систем, а также созданы основы теории оптимального управления. В настоящее время повышение значимости теории автоматического управления обусловлено еще и тем, что принципы управления, определяющие функционирование технических объектов, во многом аналогичны тем законам, по которым развиваются биологические, экономические и социальные системы. Это обуславливает возможность формирования обобщенной теории управления, подтверждающей слова французского ученого Блеза Паскаля: «Не следует себя обманывать: мы являемся в такой же степени автоматами, в какой и мыслящими существами…»
Классификация СAУ Системы автоматического регулирования классифицируются по различным признакам. 1. По принципу построения, различают разомкнутые системы, системы с управлением по отклонению (с обратной связью) и системы с компенсацией возмущения. В разомкнутых системах (см. рис. 1.1) управляющее воздействие U(t), формируемое на выходе УУ, определяется только входным сигналом системы хвх(t) и не зависит от выходной величины объекта регулирования хвых(t). При наличии значительных возмущений или нестабильности параметров системы фактический закон изменения выходной величины может значительно отклоняться от заданного. В соответствии с принципом управления по отклонению управляющее воздействие U(t) зависит от отклонения фактического закона изменения регулируемой величины от требуемого. Сигнал х(t) = хвх(t) - хвых(t), называемый ошибкой регулирования, формируется на элементе сравнения (ЭС). Информация о текущем значении регулируемой величины поступает в ЭС по каналу обратной связи (ОС). Наличие канала ОС делает структуру системы замкнутой (рис. 1.2.).
2. По виду входного сигнала САУ делятся на: системы стабилизации, входной сигнал которых является постоянной величиной (например, системы автоматической стабилизации скорости резания при металлообработке или системы стабилизации напряжения); системы программного управления, в которых входной сигнал является известной, заранее заданной функцией времени (например, система управления станков с ЧПУ); следящие системы, в которых входной сигнал заранее не определен и зачастую случаен (например, радиолокационные системы автоматического сопровождения цели). 3. Существенным при математическом описании систем является их деление на линейные и нелинейные. Для линейных систем выполняется принцип суперпозиции, суть которого заключается в следующем: если на вход системы поступает управляющее воздействие, которое можно представить в виде суммы k простых воздействий
то реакция системы (ее выходной сигнал) равна сумме реакций на каждое слагаемое хвхi(t), Все реальные системы в технике и в природе, как правило, являются в большей или в меньшей степени нелинейными. Системы, нелинейность которых проявляется незначительно, можно, с приемлемой для практики точностью, описывать как линейные, используя более простые линеаризованные характеристики и уравнения. Очевидно, что для существенно нелинейных систем использование линеаризованных моделей недопустимо, и такие системы должны рассматриваться отдельно. 4. Различают стационарные и нестационарные САУ. Параметры стационарных систем неизменны, а у нестационарных параметры являются функциями времени или сигналов системы. 5. По виду зависимости регулируемой величины от внешнего воздействия различают статические и астатические САУ. В последних, после завершения переходного процесса, вызванного внешним воздействием, значение регулируемой величины устанавливается равным заданному, т.е. в установившемся режиме ошибка регулирования равна нулю. В статических САУ регулируемая величина по окончании переходного процесса принимает значение, пропорциональное внешнему воздействию, при этом установившееся значение ошибки регулирования отлично от нуля. 6. Система относится к непрерывным, если все сигналы в ней являются непрерывными функциями времени. В дискретных САУ имеет место дискретный способ передачи и преобразования сигналов. Важнейшим классом дискретных систем являются цифровые системы, в структуру которых входят цифровые вычислительные устройства (контроллеры, микропроцессоры и т.п.). 7. В адаптивных САУ управляющее устройство позволяет обеспечить изменение алгоритмов управления и параметров системы (например, коэффициентов усиления звеньев), в результате чего достигается высокое качество работы системы. Неминимально-фазовые звенья Мы рассмотрели наиболее часто встречающиеся на практике типы минимально-фазовых звеньев. В отличие от них передаточная функция любого неминимально-фазового звена имеет хотя бы один «правый» ноль или полюс. Приведем пример такой передаточной функции:
Здесь имеется положительный полюс (корень знаменателя):
Частотные характеристики такого звена:
так как при В то же время для обычного апериодического звена имеем:
Разница между ними, как видим, в величине фазы, амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудно-частотной характеристике всегда можно определить амплитудно-фазовую и наоборот. Этим же свойством обладают вещественная Заметим, что для данного неминимально-фазового звена переходная функция будет расходящейся, вместо обычной затухающей. 2.6. Эквивалентные преобразования структурных схем линейных САУ В САУ встречаются три вида соединений звеньев: последовательное, параллельное и соединение звеньев по схеме с обратной связью. В системе, состоящей из n последовательно соединенных звеньев (рис. 2.28) выходной сигнал предыдущего звена равен входному сигналу последующего.
xвых1(p) = W1(p)xвх(p); xвых 2 (p) = W2(p) xвых 1 (p); … xвых(p) = Wn(p)xвых(n)(p).
Откуда xвых Следовательно, передаточная функция системы примет вид:
Таким образом, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев. Частотные характеристики последовательно соединенных звеньев:
где A(ω) = A1(ω)A2(ω)…An(ω); Логарифмическая амплитудно-частотная характеристика звеньев, соединенных последовательно:
Следовательно, логарифмические амплитудно- и фазо-частотная характеристики системы, состоящей из последовательно соединенных звеньев, равны сумме ЛАХ и ФЧХ отдельных звеньев. Это существенно упрощает построение логарифмических частотных характеристик, по сравнению с обычными характеристиками. Передаточная функция минимально-фазовой системы в общем случае может быть записана в виде:
В выражении (2.59) сомножители в числителе · сомножитель · сомножитель · сомножитель Аналогичные сомножители в знаменателе выражения (2.59) · сомножитель · сомножитель · сомножитель Очевидно, что в зависимости от соотношения s и Формально передаточная функция (2.59) представляет собой произведение нескольких сомножителей, что соответствует последовательному соединению звеньев, и для вычисления На оси частот в порядке возрастания указываются все частоты сопряжения Построение ЛАХ начинается на частотах, меньших самой малой частоты сопряжения Если при этом в выражении (2.59) выполняется равенство s = Если в выражении (2.59) s
т.е. ЛАХ до наименьшей частоты сопряжения Если в выражении (2.48) s =
и наклон ЛАХ до наименьшей частоты сопряжения Для построения низкочастотной асимптоты ЛАХ необходимо для произвольной частоты На частоте
Если сомножитель вида В случае, когда Таким же образом характеристика продолжается в сторону увеличения частоты, претерпевая соответствующие изломы на каждой сопрягающей частоте Примеры построения ЛАХ по различным передаточным функциям приведены на рис. 2.29. В системе, состоящей из n параллельно соединенных звеньев (рис. 2.30), на вход каждому из звеньев подается один и тот же сигнал xвх(p), а их выходные сигналы суммируются:
Так как
……………………………
то
xвых(p) = xвых 1 (p) +xвых 2 (p)+…+xвых(n)(p) =  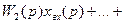  . .
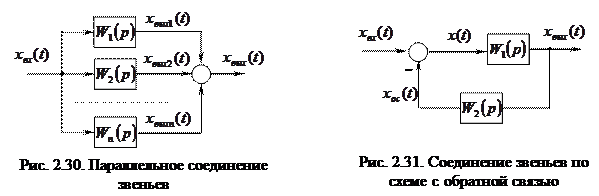
Таким образом, передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев: W(p) = Очевидно, что в случае, когда выходной сигнал какого-либо из параллельно соединенных звеньев поступает в сумматор со знаком «минус», передаточная функция этого звена входит в (2.62) также со знаком «минус». Рассмотрим структуру системы с обратной связью (рис. 2.31). На вход звена, охваченного обратной связью, подается сигнал рассогласования, равный:
Поскольку Изображение выходного сигнала: xвых(р)= откуда
Следовательно, передаточная функция замкнутой системы (в замкнутом состоянии) описывается следующим выражением: Ф(p) = Передаточная функция (2.63) найдена для случая отрицательной обратной связи. Если обратная связь положительная, то Ф(p) = При анализе и синтезе CАУ, наряду с передаточной функцией (2.63) – (2.64), используются передаточная функция разомкнутой системы и передаточная функция по ошибке. Передаточная функция разомкнутой системы (замкнутой системы в разомкнутом состоянии): W(p) = Передаточная функция по ошибке: Фx(p) =
Вопросы для самопроверки 1. Является ли блок умножения двух сигналов линейным звеном? В случае отрицательного ответа приведите линеаризованное описание этого звена в отклонениях. 2. Сформулируйте основные теоремы преобразования Лапласа. 3. Дайте определение передаточной функции САУ. 4. Как передаточная функция линейной системы зависит от входного сигнала? 5. Как определяются нули и полюса передаточной функции системы? Чему равен порядок передаточной функции системы? 6. 6.С чем связана физическая реализуемость САУ? 7. Какие системы являются минимально-фазовыми? 8. Что называется переходной функцией системы? Как переходная функция связана с функцией веса системы? 9. Как связаны между собой передаточная функция и функция веса системы? 10. Что описывают частотные характеристики САУ? 11. Как связаны передаточная функция и амплитудно-фазовая характеристика линейной системы? 12. Назовите основные виды соединения звеньев в САУ? 13. Чему равна передаточная функция замкнутой системы в разомкнутом состоянии? 14. Дайте определение передаточной функции замкнутой системы по ошибке.
Запасы устойчивости
Различают запас устойчивости по фазе и усилению. Запасы устойчивости определяются на двух частотах: частоте среза ωс и критической частоте ωкр. На частоте среза амплитудно-частотная характеристика разомкнутой системы | W(jω)| равна единице, а на критической частоте фазо-частотная характеристика этой системы φ(ω) принимает значение, равное -π. Запас устойчивости по фазе Δφ показывает, насколько фазо-частотная характеристика разомкнутой системы на частоте среза ωс отличается от -π (рис. 3.9): Δφ = π – Величина запаса устойчивости по усилению может быть определена на частоте ωкр, как разность:
либо как отношение α = 1/ | W(jωкр)|.
Системы, годографы W(jω) которых пересекают вещественную ось только справа от точки с координатами (-1, j0)(рис. 3.10, а), называют абсолютно устойчивыми. В таких системах неустойчивость может наступить только при увеличении коэффициента усиления. Если годограф частотной характеристики W(jω) разомкнутой системы пересекает вещественную ось и слева от точки с координатами (-1, j0), то систему называют условно устойчивой (рис. 3.10, б). Неустойчивой такая система может быть как при увеличении, так и при уменьшении коэффициента усиления. Для нормальной работы САУ необходимо, чтобы запас устойчивости по усилению α был не менее двух, а запас устойчивости по фазе – от 0,5 до 1 рад. 3.5. Оценка устойчивости по логарифмическим Оценку устойчивости замкнутой САУ можно осуществлять по логарифмическим амплитудно- и фазо-частотным характеристикам системы в разомкнутом состоянии: L(ω) и φ(ω). В том случае, когда годограф W(jω) не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие ωс < ωкр.
На рис. 3.11 приведены ЛАХ и ФЧХ устойчивых разомкнутых системы, одна из которых при замыкании остается устойчивой (рис. 3.11, а), а другая – становится неустойчивой (рис. 3.11, б). По L(ω) и φ(ω) разомкнутой системы можно определить запасы устойчивости: запас по фазе Δφ отсчитывают по фазо-частотной характеристике на частоте среза ωс, а запас устойчивости по усилению ΔL равен значению ЛАХ на критической частоте ωкр, взятому с обратным знаком, т.е. ΔL = | L(ωкр)| (см. рис. 3.11, а). Если ωс = ωкр, то система находится на границе устойчивости. Если при некотором значении коэффициента усиления (k) замкнутая система устойчива с запасом устойчивости по усилению равным ΔL, то величина критического коэффициента усиления kкр может быть вычислена по формуле: 20lg kкр = 20lg k + ΔL. Для оценки устойчивости условно устойчивых САУ реальных технических систем, имеющих обычно достаточно сложную форму, также можно воспользоваться понятием перехода. При этом переходом называется пересечение графика φ(ω) с горизонтальной прямой -π, при условии, что на частоте, при которой φ(ω) = – π, ЛАХ положительна. Правило определения знака перехода противоположно рассмотренному для W(jω): переход графика φ(ω) через уровень(- π) считается положительным, если при увеличении частоты ω пересечение этого уровня происходит снизувверх, в противном случае переход считается отрицательным. Обозначим число положительных переходов m+, а число отрицательных переходов m- . В этом случае формулировка критерия устойчивости Найквиста: система в замкнутом состоянии становится устойчивой, если разность между числом положительных и отрицательных переходов равна m/ 2, т.е. m+ – m- = m/ 2, (3.23) где m – число правых полюсов разомкнутой системы. Если число положительных переходов φ(ω) равно числу отрицательных, то система, устойчивая в разомкнутом состоянии
Рекомендации для обеспечения запаса устойчивости, которые следуют из практики проектирования САУ: · во-первых, для того чтобы в системе были обеспечены необходимые запасы устойчивости, наклон ЛАХ в диапазоне частот, в котором расположена частота среза, должен быть равен -20 дБ/дек. Если в указанном частотном диапазоне наклон L(ω) равен -40 дБ/дек, обеспечить необходимый запас устойчивости по фазе затруднительно. При наклоне 0 дБ/дек система обладает чрезмерно большим запасом устойчивости по фазе и становится передемпфированной с длительным переходным процессом: · во-вторых, запас устойчивости системы по фазе зависит от диапазона частот, в котором ЛАХ разомкнутой системы в области частоты среза имеет наклон -20 дБ/дек. Чем шире этот диапазон частот, тем выше запас устойчивости по фазе и наоборот. Вопросы для самопроверки 1. Дайте определение устойчивости САУ. 2. Сформулируйте необходимое условие устойчивости системы. 3. Поясните различие между прямым и косвенным методами оценки устойчивости. 4. Что такое критерии устойчивости? Каким образом они связаны с необходимым и достаточным условиями устойчивости? 5. Что такое граница устойчивости? Как по отношению к ней расположены полюса устойчивой системы? 6. Сформулируйте критерий устойчивости Гурвица. 7. Каким образом по критерию Гурвица вычисляется критический коэффициент усиления и запас устойчивости по усилению? 8. Сформулируйте критерий устойчивости Найквиста. 9. Что такое частота среза и критическая частота? Каким образом определяются эти частоты по годографам АФХ и ЛАФЧХ? 10. Что такое запасы устойчивости? Каким образом они определяются по годографам АФХ и ЛАФЧХ? 11. Как по ЛАЧХ определяется критический коэффициент усиления? 12. Как по ЛАФЧХ определяется критическое время запаздывания? Частотные критерии качества Оценка динамических свойств САУ по ее переходной функции h(t) представляет собой прямой метод исследования качества регулирования. Существует возможность судить об основных показателях качества переходных процессов в системе и без построения h(t), используя различные косвенные оценки, которые определяются проще, чем переходная функция. Такие косвенные оценки называются критериями качества. При исследовании качества переходных процессов эти критерии являются аналогами критериев устойчивости. Рассмотрим частотные критерии качества, позволяющие судить о динамических свойствах системы по ее частотным характеристикам. К их числу могут быть отнесены (см. разд. 3.4) запасы устойчивости САУ по усилению и фазе, которые могут быть определены по АФХ или логарифмическим амплитудно- и фазо-частотной характеристикам системы в разомкнутом состоянии. Для оценки качества переходного процесса минимально-фазовой системы достаточно знать вид ее амплитудно-частотной характеристики
При этом АЧХ нормированных статических систем К частотным показателем качества, определяемым по · полоса пропускания системы · резонансная частота · показатель колебательности M. Полоса пропускания системы Резонансная частота
При
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.013 с.) |


 В системах с компенсацией возмущения (рис. 1.3.) управляющее воздействие U(t) на выходе УУ зависит как от входного сигнала системы хвх(t), так и от возмущающего воздействия хвозм(t).
В системах с компенсацией возмущения (рис. 1.3.) управляющее воздействие U(t) на выходе УУ зависит как от входного сигнала системы хвх(t), так и от возмущающего воздействия хвозм(t).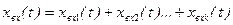 ,
, При этом значение k и форма хвхi(t) могут быть любыми.
При этом значение k и форма хвхi(t) могут быть любыми.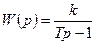 .
.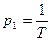 .
.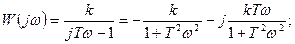
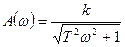 ;
; 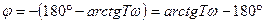 ,
, входной и выходной гармонические сигналы находятся в противофазе.
входной и выходной гармонические сигналы находятся в противофазе.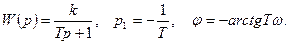
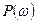 и мнимая
и мнимая 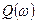 части амплитудно-фазовой характеристики минимально-фазовых звеньев.
части амплитудно-фазовой характеристики минимально-фазовых звеньев.
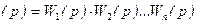 xвх(p).
xвх(p).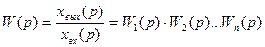 . (2.57)
. (2.57)
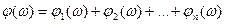 .
.
 . (2.58)
. (2.58)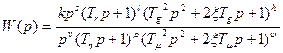 . (2.59)
. (2.59)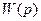 определяют нули передаточной функции, а именно:
определяют нули передаточной функции, а именно: соответствует нулевому нолю кратности
соответствует нулевому нолю кратности 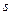 ,
,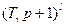 – действительному нолю
– действительному нолю 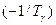 кратности l,
кратности l, – паре комплексно-сопряженных нолей кратности
– паре комплексно-сопряженных нолей кратности 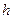 .
.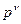 соответствует нулевому полюсу кратности
соответствует нулевому полюсу кратности 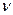 ,
,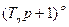 – действительному полюсу
– действительному полюсу  кратности
кратности 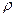 ,
, – паре комплексно-сопряженных полюсов кратности
– паре комплексно-сопряженных полюсов кратности 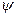 .
.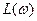 можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.
можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.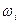 ЛАХ, определяемые соответствующими постоянными времени:
ЛАХ, определяемые соответствующими постоянными времени: 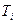 .
.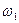 .
.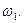
 , а
, а  , (2.60)
, (2.60)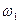 проводится с наклоном (+20∙ s) дБ/дек.
проводится с наклоном (+20∙ s) дБ/дек. , а
, а 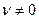 , то уравнение низкочастотной асимптоты:
, то уравнение низкочастотной асимптоты: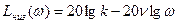 , (2.61)
, (2.61)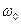 меньшей или равной
меньшей или равной 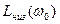 и через точку с координатами (
и через точку с координатами (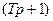 в числителе передаточной функции (2.59).
в числителе передаточной функции (2.59).
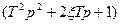 , происходит изменение предыдущего наклона на +40∙ h, если указанный сомножитель присутствует в числителе
, происходит изменение предыдущего наклона на +40∙ h, если указанный сомножитель присутствует в числителе 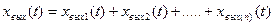 .
. ;
;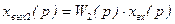 ;
;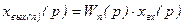 ,
,
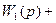
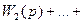
 . (2.62)
. (2.62)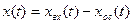 .
.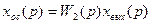 , то
, то 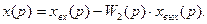
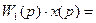

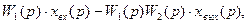
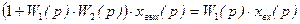 .
.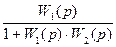 . (2.63)
. (2.63)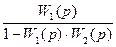 . (2.64)
. (2.64) . (2.65)
. (2.65)

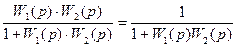 . (2.66)
. (2.66)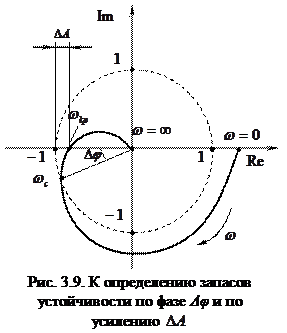 В процессе эксплуатации САУ ее параметры (коэффициенты усиления, постоянные времени) из-за изменения внешних условий, колебаний напряжений источников энергии и других причин отличаются от расчетных значений. Если не принять определенных мер, то исходная устойчивая система может стать неустойчивой. Для исключения этого явления при проектировании следует обеспечить определенные запасы устойчивости системы, которые характеризуют близость годографа амплитудно-фазовойхарактеристики разомкнутой системы W(jω) к точке с координатами (-1, j0).
В процессе эксплуатации САУ ее параметры (коэффициенты усиления, постоянные времени) из-за изменения внешних условий, колебаний напряжений источников энергии и других причин отличаются от расчетных значений. Если не принять определенных мер, то исходная устойчивая система может стать неустойчивой. Для исключения этого явления при проектировании следует обеспечить определенные запасы устойчивости системы, которые характеризуют близость годографа амплитудно-фазовойхарактеристики разомкнутой системы W(jω) к точке с координатами (-1, j0).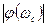 .
. = 1 – | W(jωкр)|,
= 1 – | W(jωкр)|,

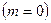 , остается устойчивой при замыкании. На рис. 3.12 в качестве примера приведены логарифмические амплитудно- и фазо-частотные характеристики неустойчивой разомкнутой системы, имеющей два правых полюса
, остается устойчивой при замыкании. На рис. 3.12 в качестве примера приведены логарифмические амплитудно- и фазо-частотные характеристики неустойчивой разомкнутой системы, имеющей два правых полюса 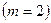 . При замыкании такая система становится устойчивой, так как m+ = 1, а m- = 0, и условие (3.23) выполняется.
. При замыкании такая система становится устойчивой, так как m+ = 1, а m- = 0, и условие (3.23) выполняется.
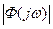 . С целью обеспечения сопоставимости значений критериев для различных САУ характеристика
. С целью обеспечения сопоставимости значений критериев для различных САУ характеристика 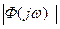 нормируется, для чего ее ординаты делятся на начальное значение
нормируется, для чего ее ординаты делятся на начальное значение  , т.е. на ее значение при
, т.е. на ее значение при 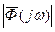

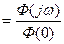 .
.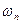 ;
; :
: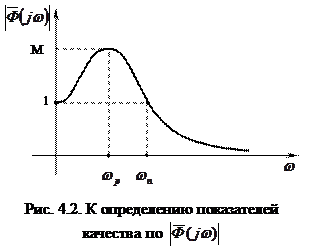 Показатель колебательности M равен максимальному значению нормированной АЧХ замкнутой системы, т.е.
Показатель колебательности M равен максимальному значению нормированной АЧХ замкнутой системы, т.е. =
=  .
. < 1 переходная функция системы монотонная (не колебательная). Чем больше M, тем больше колебательность. При M
< 1 переходная функция системы монотонная (не колебательная). Чем больше M, тем больше колебательность. При M 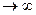 в системе возникают незату
в системе возникают незату 


