
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели качества процесса регулированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Устойчивость САУ является необходимым, но не достаточным условием эффективного функционирования системы. Не менее важно, чтобы процесс регулирования осуществлялся при обеспечении определенных показателей качества. Требования к качеству переходного процесса могут быть самыми разнообразными, однако к числу наиболее существенных критериев, с помощью которых оценивается поведение системы в динамике, относятся следующие: · показатели качества переходного процесса, определяемые по переходной функции системы; · частотные критерии качества; корневые критерии качества; · интегральные критерии качества. Поскольку переходный процесс в системе определяется не только параметрами САУ, но и характером внешнего воздействия, оценку качества регулирования осуществляют по виду реакции системы на типовой входной сигнал. Наиболее часто характер протекания переходного процесса оценивается по переходной функции системы. Основными показателями качества процесса регулирования, определяемыми по переходной функции системы (рис. 4.1), являются: время регулирования (tp), перерегулирование (σ), частота (ω)и число колебаний.
Обычно принимают Перерегулированием σ называется максимальное отклонение регулируемой величины Абсолютная величина отклонения определяется по графику переходной функции:
Соответственно перерегулирование равно:
Допустимое значение перерегулирования определяется спецификой функционирования конкретной системы. Обычно оно составляет 10 – 30 %, но для ряда САУ перерегулирование принципиально недопустимо. Колебательность переходного процесса определяется числом колебаний регулируемой величины за время регулирования tp, например, числом минимумов за этот интервал. Приемлемым считается от одного до трех колебаний. Иногда колебательность определяют, как отношение величин первого ( Частота колебаний равна:
где T – период колебаний. В случае необходимости к перечисленным показателям качества процесса регулирования добавляются следующие: время достижения первого максимума
и ряд других. Частотные критерии качества Оценка динамических свойств САУ по ее переходной функции h(t) представляет собой прямой метод исследования качества регулирования. Существует возможность судить об основных показателях качества переходных процессов в системе и без построения h(t), используя различные косвенные оценки, которые определяются проще, чем переходная функция. Такие косвенные оценки называются критериями качества. При исследовании качества переходных процессов эти критерии являются аналогами критериев устойчивости. Рассмотрим частотные критерии качества, позволяющие судить о динамических свойствах системы по ее частотным характеристикам. К их числу могут быть отнесены (см. разд. 3.4) запасы устойчивости САУ по усилению и фазе, которые могут быть определены по АФХ или логарифмическим амплитудно- и фазо-частотной характеристикам системы в разомкнутом состоянии. Для оценки качества переходного процесса минимально-фазовой системы достаточно знать вид ее амплитудно-частотной характеристики
При этом АЧХ нормированных статических систем К частотным показателем качества, определяемым по · полоса пропускания системы · резонансная частота · показатель колебательности M. Полоса пропускания системы Резонансная частота
При Длительность переходного процесса определяется шириной характеристики Величина перерегулирования может быть приближенно оценена по виду вещественной частотной характеристики замкнутой системы:
Если график Колебательность и длительность переходного процесса h(t) замкнутой системы могут быть в первом приближении определены по параметрам ЛАХ разомкнутой системы: частоте среза и величинам запасов устойчивости по фазе и амплитуде. В случае колебательной переходной функции h(t) резонансная частота ωр замкнутой системы близка по величине к частоте среза Корневые критерии качества Эта группа критериев позволяет оценить качество переходных процессов по расположении полюсов и нулей передаточной функции устойчивой замкнутой системы. При исследовании устойчивости САУ оценивалось только расположение полюсов на комплексной плоскости. Оценивая качество переходного процесса, необходимо учитывать и расположение нулей. К числу корневых критериев качества относят степень устойчивости и степень колебательности. Степень устойчивости (η) – это расстояние от мнимой оси до ближайшего к ней левого полюса (рис. 4.3, а) или ближайшей пары комплексно сопряженных полюсов замкнутой системы (рис. 4.3, б). В первом случае соответствующая этому полюсу слагаемое в общем решении дифференциального уравнения (3.5) равно:
В обоих случаях указанное слагаемое будет затухать медленнее остальных, тем самым определяя в первом приближении длительность переходного процесса: Степень колебательности определяется только для замкнутых систем, передаточные функции имеют комплексно-сопряженные полюса: pi,i+1 = αi + jβi. Переходная функция таких систем в большей или меньшей степени колебательна. Степень колебательности переходного процесса равна:
где φ – наибольший по величине угол, образованный отрицательной вещественной полуосью и лучом, проведенным из начала координат к комплексному полюсу pi Задавшись предельно допустимыми значениями степени устойчивости ηз и степени колебательности φз, можно построить на комплексной плоскости область (рис. 4.3, в), в которой должны находиться полюса системы, показатели качества регулирования которой будут удовлетворять заданным значениям, т.е. η > ηз и μ < μз.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 6276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.245.158 (0.009 с.) |


 от ее установившегося значения
от ее установившегося значения  не превышает наперед заданной величины
не превышает наперед заданной величины  .
. Таким образом, время регулирования определяет длительность переходного процесса, т.е. быстродействие системы. Величина tp должна быть ограничена не только сверху, но и снизу, поскольку при повышении быстродействия системы время регулирования уменьшается, но при этом возрастают динамические нагрузки, что отрицательно сказывается на сроке службы САУ.
Таким образом, время регулирования определяет длительность переходного процесса, т.е. быстродействие системы. Величина tp должна быть ограничена не только сверху, но и снизу, поскольку при повышении быстродействия системы время регулирования уменьшается, но при этом возрастают динамические нагрузки, что отрицательно сказывается на сроке службы САУ. от установившегося значения
от установившегося значения  , выраженное в процентах.
, выраженное в процентах.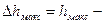
 ℅. (4.1)
℅. (4.1) ) и второго (
) и второго (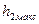 ) максимумов переходной функции выраженное в процентах.
) максимумов переходной функции выраженное в процентах.
 , время первого достижения уровня установившегося значения
, время первого достижения уровня установившегося значения  , декремент затухания, равный:
, декремент затухания, равный: ,
,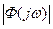 . С целью обеспечения сопоставимости значений критериев для различных САУ характеристика
. С целью обеспечения сопоставимости значений критериев для различных САУ характеристика 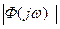 нормируется, для чего ее ординаты делятся на начальное значение
нормируется, для чего ее ординаты делятся на начальное значение  , т.е. на ее значение при
, т.е. на ее значение при  :
: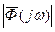

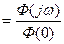 .
.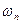 ;
; :
: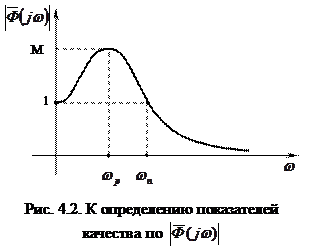 Показатель колебательности M равен максимальному значению нормированной АЧХ замкнутой системы, т.е.
Показатель колебательности M равен максимальному значению нормированной АЧХ замкнутой системы, т.е. =
=  .
. < 1 переходная функция системы монотонная (не колебательная). Чем больше M, тем больше колебательность. При M
< 1 переходная функция системы монотонная (не колебательная). Чем больше M, тем больше колебательность. При M  в системе возникают незатухающие колебания с частотой
в системе возникают незатухающие колебания с частотой  .
. .
. имеет максимум («горб»), переходный процесс в системе происходит с перерегулированием, величина которого составляет не менее 18 %. В случае монотонно убывающей характеристики
имеет максимум («горб»), переходный процесс в системе происходит с перерегулированием, величина которого составляет не менее 18 %. В случае монотонно убывающей характеристики  .
.
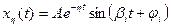 .
. .
. ,
,


